The Neuron vs the Synapse: Which One Is in the Driving Seat?

David Dahmen

Viewpoint

The Neuron vs the Synapse: Which One Is in the Driving Seat?

Institute for Advanced Simulation, Jülich Research Centre, Germany

April 1, 2024• Physics 17, 50

A new theoretical framework for plastic neural networks predicts dynamical regimes where synapses rather than neurons primarily drive the network’s behavior, leading to an alternative candidate mechanism for working memory in the brain.

Figure caption — **Figure 1:** When the dynamics of neurons and synapses in a neural network can equally influence the dynamics of the whole network, specific neuronal activity patterns can dynamically arise. These patterns become stable if the synaptic dynamics halts, “freezing” neuronal states until synaptic dynamics resume.

The brain is an immense network of neurons, whose dynamics underlie its complex information processing capabilities. A neuronal network is often classed as a complex system, as it is composed of many constituents, neurons, that interact in a nonlinear fashion (Fig. 1). Yet, there is a striking difference between a neural network and the more traditional complex systems in physics, such as spin glasses: the strength of the interactions between neurons can change over time. This so-called synaptic plasticity is believed to play a pivotal role in learning. Now David Clark and Larry Abbott of Columbia University have derived a formalism that puts neurons and the connections that transmit their signals (synapses) on equal footing [1]. By studying the interacting dynamics of the two objects, the researchers take a step toward answering the question: Are neurons or synapses in control?

Clark and Abbott are the latest in a long line of researchers to use theoretical tools to study neuronal networks with and without plasticity [2, 3]. Past studies—without plasticity—have yielded important insights into the general principles governing the dynamics of these systems and their functions, such as classification capabilities [4], memory capacities [5, 6], and network trainability [7, 8]. These works studied how temporally fixed synaptic connectivity in a network shapes the collective activity of neurons. Adding plasticity to the system complicates the problem because then the activity of neurons can dynamically shape the synaptic connectivity [9, 10].

The reciprocal interplay between neuronal and synaptic dynamics in a neuronal network is further obscured by the multiple timescales both types of dynamics can span. Most previous efforts to theoretically investigate the collective behavior of such a network with plasticity assumed there were two distinct sets of timescales for the neuronal and synaptic dynamics, with one of the two being roughly constant. Thus, the question of how such a network would behave if the neuronal and synaptic dynamics evolved in parallel remained open.

In developing their formalism, Clark and Abbott turned to dynamic mean-field theory, a method originally devised for studying disordered systems. They extended the theory so that it incorporates synaptic dynamics alongside neuronal dynamics. They then devised a simple model that qualitatively accounts for various important ingredients of plastic neuronal networks: a nonlinear neuronal input-to-output transfer, distinct timescales for neuronal and synaptic dynamics, and a control parameter that tunes the level and type of plasticity in the network.

The researchers find that synaptic dynamics play a major role in shaping the overall behavior of a neuronal network when the synaptic and neuronal dynamics evolve on a similar timescale. In fact, Clark and Abbott show that they can tune how much the dynamics of the neurons and synapses each contribute to the dynamics of the overall network. Interestingly, the analysis reveals that for strong Hebbian plasticity [9]—a type of plasticity driven by the increase in efficacy of a synapse when its connecting neurons are simultaneously active—synaptic dynamics drive the network’s global behavior, underlining the importance of its incorporation.

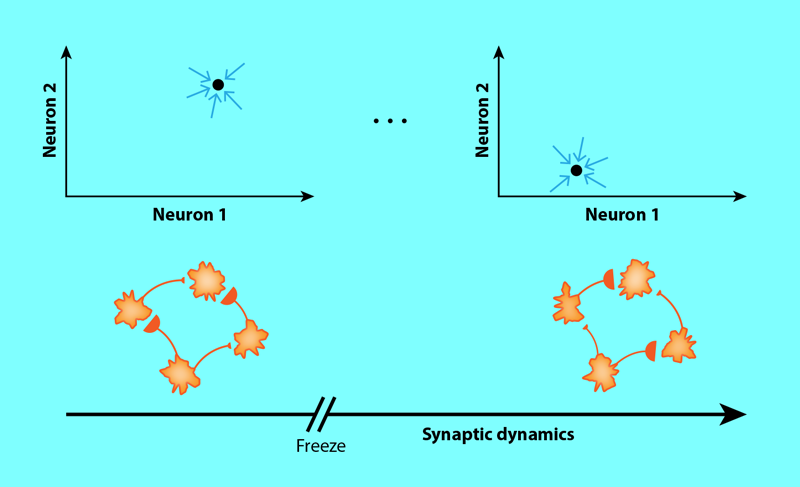
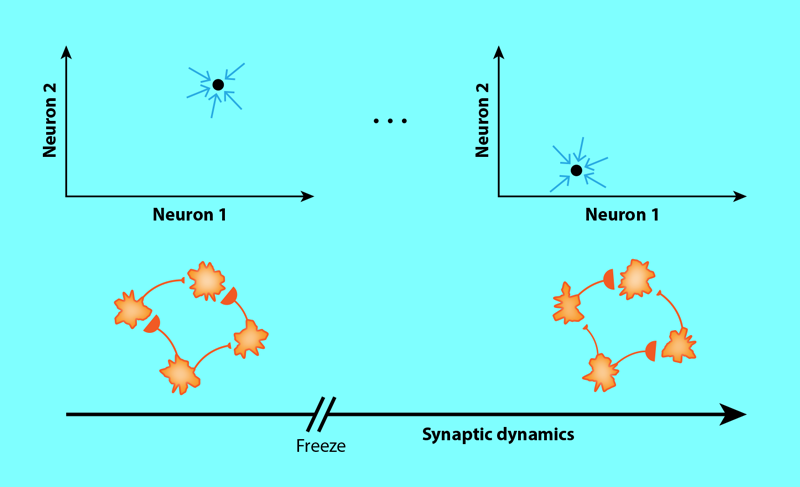
The model also links the strength and nature of plasticity in the network to changes of a key dynamical property of such a network: how chaotic it is. Chaotic networks exhibit self-sustained variable activity that is highly sensitive to perturbations. Clark and Abbott show that, depending on the strength, synaptic dynamics can accelerate or slow down neuronal dynamics and promote or suppress chaos. The researchers also observe a particularly interesting and qualitatively new behavior, which arises when the synapses dynamically generate specific favorable neuronal activity patterns (fixed points) in the network. These fixed points can “freeze in” when plasticity is turned off, causing the states of the neurons to stay constant (Fig. 2). The states only resume the ability to change when plasticity is turned back on. The researchers term this behavior freezable chaos. In freezing the state of the neurons, freezable chaos can serve as a mechanism to store information that is reminiscent of how working memory is thought to operate.

This prediction, as well as the proposals of experiments to disentangle freezable chaos from other predicted working memory mechanisms, is a key advance of the new study and paves the way for many more exciting works in the future. One goal of such work is understanding how the brain processes external inputs from sensory stimuli. Clark and Abbott consider the dynamics of their neuronal network in the absence of any external input. Extending the model so that it can account for externally driven transient dynamics that interact with plasticity could allow researchers to predict network structures and dynamics that relate to this important brain task. Furthermore, it is important to transfer insights from this abstract neuronal network to more realistic networks that factor in biologically relevant properties of the brain, such as that neurons communicate via discrete spikes, have specifically structured connection patterns, and come in multiple distinct classes. Moving to biologically realistic networks has proved successful for past models, and we can anticipate similar successes for this new theory.

References

D. G. Clark and L. F. Abbott, “Theory of coupled neuronal-synaptic dynamics,” Phys. Rev. X 14, 021001 (2024).
R. Kempter et al., “Hebbian learning and spiking neurons,” Phys. Rev. E 59, 4498 (1999).
H. Sompolinsky et al., “Chaos in random neural networks,” Phys. Rev. Lett. 61, 259 (1988).
C. Keup et al., “Transient chaotic dimensionality expansion by recurrent networks,” Phys. Rev. X 11, 021064 (2021).
T. Toyoizumi and L. F. Abbott, “Beyond the edge of chaos: Amplification and temporal integration by recurrent networks in the chaotic regime,” Phys. Rev. E 84, 051908 (2011).
J. Schuecker et al., “Optimal sequence memory in driven random networks,” Phys. Rev. X 8, 041029 (2018).
S. S. Schoenholz et al., “Deep information propagation,” 5th International Conference on Learning Representations, ICLR 2017. arXiv:1611.01232.
F. Schuessler et al., “The interplay between randomness and structure during learning in RNNs,” in Advances in Neural Information Processing Systems, edited by H. H. Larochelle et al. (Curran Associates, New York, 2020), Vol. 33.
D. O. Hebb, “The Organization of Behavior,” (Wiley & Sons, New York, 1949).
J. C. Magee and C. Grienberger, “Synaptic plasticity forms and functions,” Annu. Rev. Neurosci. 43, 95 (2020).

About the Author

David Dahmen is a researcher in the Institute for Advanced Simulation at the Jülich Research Centre, Germany. He received his PhD from RWTH Aachen University, Germany, in 2017. His research interests include neural information processing of biological and artificial networks and the development of statistical physics and field theory approaches applied to these domains. For the past few years, Dahmen has focused on the role of heterogeneity in neural networks in shaping the collective dynamics of neurons and explaining experimentally observed patterns of neural coordination in cortical circuits.