Quasi-integrable Arrays: The Family Grows
A frictionless pendulum and a pendulum clock behave alike, but they belong to different worlds: Hamiltonian systems and dissipative systems, respectively. In the Hamiltonian world, completely integrable—that is, solvable—systems serve as a mathematical basis for dealing with more general cases that aren’t integrable. An analogous strategy doesn’t work for nonlinear non-Hamiltonian dissipative systems, however. In that case, the best researchers can achieve is partial integrability. Until recently, it was thought that an array of globally coupled oscillators could be partially integrable only if each oscillator has only one degree of freedom. Now Rok Cestnik and Erik Martens, both at Lund University in Sweden, report on a quasi-integrable system consisting of N two-dimensional oscillators described by ordinary differential equations (ODEs) [1]. The duo obtained a drastic reduction in dimensionality: from N complex-valued ODEs to three complex-valued global coordinates and N − 3 complex-valued constants of motion. Their feat could establish a base camp from which to launch attacks on more convoluted problems, such as arrays of spiking neurons or neural rate models.
Arrays of dissipative oscillators are ubiquitous in nature, from cells to ecosystems, and in technology. Unfortunately, their mathematical analysis is a frustrating challenge. Closed expressions do not even exist for one isolated oscillator. To cope with this difficulty, theorists have developed a convenient framework that works with one-degree-of-freedom oscillators, such as the integrate-and-fire model or the phase oscillator. This approach is well grounded in the so-called phase approximation, which entails removing degrees of freedom other than the phase from the equations of motion [2].
A family of globally coupled phase oscillators is amenable to exact analysis, thanks to two complementary theoretical milestones. The first was obtained in 1993 by mathematicians Shinya Watanabe and Steven Strogatz [3]. The duo proved that the dynamics of certain arrays of identical phase oscillators are quasi-integrable. The system of N oscillators can be described by N − 3 constants of motion—conserved quantities determined by the initial conditions—and by only three nontrivial degrees of freedom, which obey ODEs. The latter degrees of freedom can fully capture the system evolution, providing an extraordinary reduction in the problem’s dimensionality. This simplification allowed theorists to explain features, including the stability of arrays of superconducting Josephson junctions [4] and arrays of quadratic integrate-and-fire (QIF) neurons [5].
The Watanabe-Strogatz theory was limited to identical oscillators. In 2008, a second, complementary theory overcame this restriction. Theorists Edward Ott and Thomas Antonsen found an exact dimensionality-reduction scheme for ensembles of heterogeneous oscillators [6]. The Ott-Antonsen theory was initially applied to an ensemble of phase oscillators known as the Kuramoto model [2]. Researchers went on to include interactions through pulses in phase models. In 2015, Ernest Montbrió, Alex Roxin, and I showed that a scheme equivalent to that of Ott and Antonsen’s could describe ensembles of heterogeneous QIF neurons in terms of a biologically meaningful global variable, the firing rate [7].
The Watanabe-Strogatz and Ott-Antonsen theories might seem unrelated. The first applied to finite arrays of identical oscillators, whereas the second was valid for infinite heterogeneous oscillators. However, physicists Arkady Pikovsky and Michael Rosenblum soon discovered a link: the Ott-Antonsen scheme is tantamount to a uniform distribution of constants of motion in each subpopulation of identical oscillators [8].
Being stuck with one-dimensional oscillators appeared to be the inevitable price to pay for any exact reduction in dimensionality. That’s no longer the case according to the new results of Cestnik and Martens, who generalized the Watanabe-Strogatz theory to arrays of two-dimensional systems. The researchers expound their theory with three demonstrations. The first shows that the new theory includes the Watanabe-Strogatz theory as a subclass. The second shows that the theory can describe arrays of generalized QIF neurons that adopt complex-valued variables. The third example involves a complex generalization of the phase oscillator, equivalent to phase oscillators supplemented with a free amplitude.
A building block of the Cestnik-Martens theory is the complex Riccati equation, which is characterized by a quadratic nonlinearity; it is not part of the physicist’s standard toolbox. An important limitation of this ODE is that, unlike a pendulum clock, it cannot exhibit a periodic attractor (that is, an isolated limit cycle). At best, it can display a continuum of periodic orbits. Despite this limitation, Cestnik and Martens suggest that their theory might have interesting links with other models. For example, the firing-rate equation derived in [7] turns out to be a complex Riccati equation. Although this is only true when self-coupling vanishes, perturbation theory on top of Cestnik-Martens quasi-integrability might allow us to describe arrays of rate neurons, a basic setup in computational neuroscience.
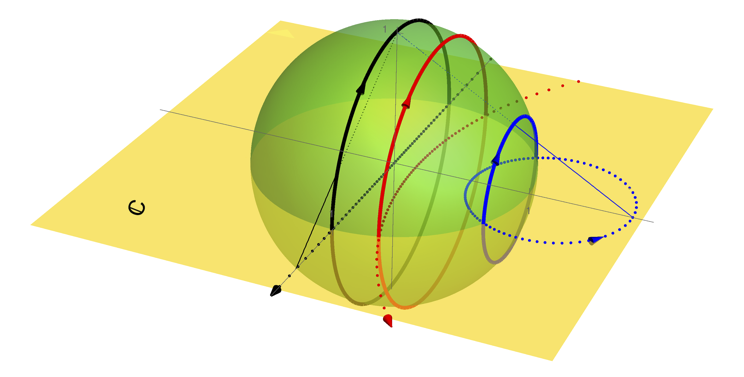
Cestnik and Martens envisage higher-dimensional extensions of their theory, in analogy to the generalization of the Watanabe-Strogatz theory previously developed by the mathematician Max Lohe [9] for arrays of orientable agents on a D-dimensional sphere. Orientable agents in three dimensions are used to study the alignment of velocity vectors in flocks of birds, schools of fishes, and swarms of flying drones. The phase space of the isolated unit can “choose” among a continuum of uniformly rotating solutions, plus two neutral fixed points (Fig. 1). Those dynamics and the Riccati equation are linked through a stereographic projection. Specifically, closed trajectories on the sphere map to periodic orbits of the Riccati equation on the complex plane. This mapping explains the consistency of the Cestnik-Martens theory with the results in [9]. Both array models have the potential to enrich each other. In fact, a counterpart of the Ott-Antonsen scheme for orientable agents was found [10], which could be leveraged for arrays of heterogeneous Riccati equations.
Quasi-integrable non-Hamiltonian systems are of fundamental interest because they constitute special systems amenable to dimensionality reduction. Such reductions have the potential to enable the efficient investigation of collective phenomena in any field. Finding quasi-integrability provides perhaps the most promising strategy for tackling high-dimensional nonlinear systems.
References
- R. Cestnik and E. A. Martens, “Integrability of a globally coupled complex Riccati array: Quadratic integrate-and-fire neurons, phase oscillators, and all in between,” Phys. Rev. Lett. 132, 057201 (2024).
- Y. Kuramoto, Chemical oscillations, waves, and turbulence (Springer-Verlag, Berlin, 1984)[Amazon][WorldCat].
- S. Watanabe and S. H. Strogatz, “Integrability of a globally coupled oscillator array,” Phys. Rev. Lett. 70, 2391 (1993).
- S. Watanabe and S. H. Strogatz, “Constants of motion for superconducting Josephson arrays,” Phys. D: Nonlinear Phenom. 74, 197 (1994).
- C. R. Laing, “The dynamics of networks of identical theta neurons,” J. Math. Neurosc. 8, 4 (2018).
- E. Ott and T. M. Antonsen, “Low dimensional behavior of large systems of globally coupled oscillators,” Chaos 18, 037113 (2008).
- E. Montbrió et al., “Macroscopic description for networks of spiking neurons,” Phys. Rev. X 5, 021028 (2015).
- A. Pikovsky and M. Rosenblum, “Partially integrable dynamics of hierarchical populations of coupled oscillators,” Phys. Rev. Lett. 101, 264103 (2008).
- M. A. Lohe, “Higher-dimensional generalizations of the Watanabe–Strogatz transform for vector models of synchronization,” J. Phys. A: Math. Theor. 51, 225101 (2018).
- S. Chandra et al., “Complexity reduction ansatz for systems of interacting orientable agents: Beyond the Kuramoto model,” Chaos 29, 053107 (2019).