How Migration May Stabilize the Diversity of Ecosystems
Dietrich Stauffer, one of the most prolific researchers in statistical physics, famously defended the value of applying ideas from physics to other disciplines—including economics, sociology, and even psychology [1]. In 2004, he wrote that many fields, including biology in particular, weren’t yet open to these physics-based approaches but foresaw that the situation would change. Two decades of multidisciplinary research have vindicated his vision. Physics-based descriptions of complex systems have since been used to study pedestrian behavior and design optimal evacuation strategies [2], to understand markets and economic systems [3], or to model epidemics and have led to the development of the new field of computational social science [4]. Now the work by Giulia Garcia Lorenzana and Giulio Biroli of Sorbonne University, France, and Ada Altieri of Paris City University offers an example of a potentially powerful application of physics to ecology [5]. Using methods from statistical physics, the trio’s new model sheds light on how complex ecosystems can maintain both diversity (host a richness of species) and stability (avoid wild species fluctuations and extinctions).
This stability–complexity issue has been debated since the 1970s [6], triggered by the seminal work of theoretical ecologist Robert May (who, incidentally, held a PhD in theoretical physics). May described ecosystems using the theory of random matrices—previously used to tackle problems in nuclear physics, such as the computation of the spectra of heavy nuclei. He concluded that large and complex ecosystems ought to be unstable [7]. May realized, however, that his conclusion was at odds with what we see in the real world and asked what “devious strategies” nature might deploy to maintain both stability and diversity.
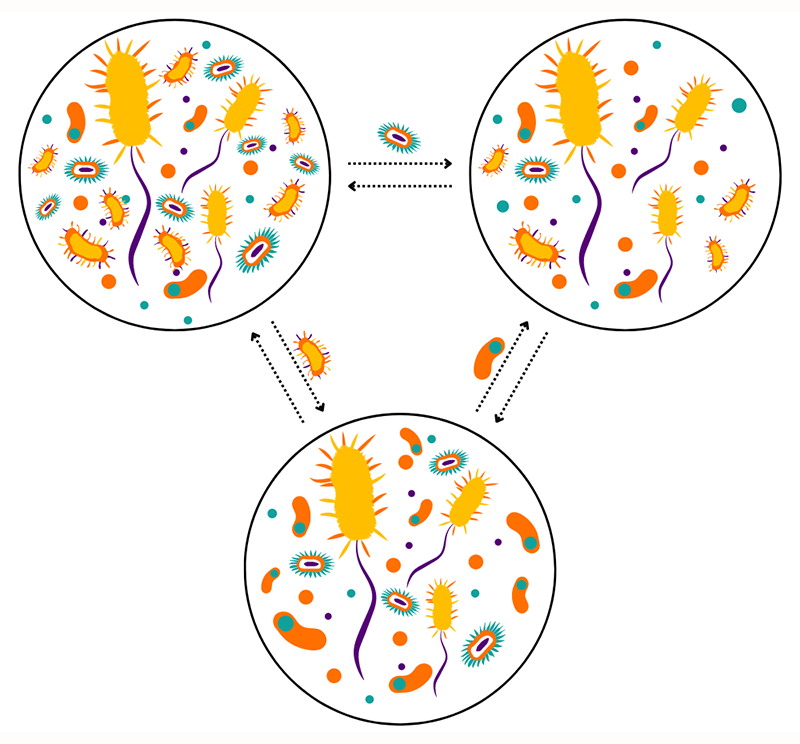
Garcia Lorenzana and her colleagues tackle this question using a statistical-field theory to model a “metacommunity”—a community comprising several local communities, each consisting of a network of interacting species (Fig. 1). Interestingly, the field theory they obtain for their model is similar to that of directed percolation, a model introduced to describe the diffusion of a liquid or gas through a porous medium and later applied to spreading phenomena such as forest fires and epidemics. Directed percolation is one of the most-studied models in nonequilibrium statistical physics, and has been vetted experimentally, with notable demonstrations with turbulent liquid crystals [8]. Their model includes essential elements of natural ecological networks: complex and diverse interactions between species (including prey–predator relationships or competition for food), the possibility of species migration between different locations, and demographic noise. Such noise captures statistical fluctuations of birth and death processes.
As previous studies have shown, demographic noise plays a particularly important role in determining the fate of small populations: species may become extinct by pure chance once there is only a small number of individuals left. However, Garcia Lorenzana and her co-workers find that species migration can offer a rescuing mechanism in the metacommunity. Namely, the extinctions can be compensated by sufficiently fast diffusion between the different patches of local communities, leading to a “recolonization” effect. The researchers predict that each species in the ecosystem displays a phase transition between a state of survival for high mobility and a state of extinction for low mobility. For large demographic noise, the team shows that interactions between species play a secondary role. Species behave roughly as if they were existing alone in the different habitats.
The researchers find that, when demographic noise is weak, the behavior of the community becomes much more complex. The large number of species in the community, combined with interspecies interactions and with the possibility to migrate, allows the metacommunity to persist even under relatively harsh conditions that would lead to extinction if the species were isolated from one another. This is possible because of the spontaneous emergence of collective effects through which the community becomes more resilient. Species that are mostly detrimental to other species are eliminated, while a stabilizing “mutualism” emerges in the community: the surviving species cooperate with one another, ensuring each other’s survival.
The transition between an extinction state at low mobility and a survival state for large diffusion constants persists with weak demographic noise. However, Garcia Lorenzana and collaborators find that, in contrast to a situation with large noise, the phase transition becomes discontinuous, with an intermediate, metastable regime that displays hysteresis and tipping-point behavior. In this regime, small perturbations of the community can lead to irreversible, catastrophic shifts of the total population of the metacommunity. The researchers suggest that their model could be used to find early signals, or precursors, of the system approaching a tipping point—potentially allowing for interventions before the catastrophic shift occurs. They propose that monitoring certain observables related to the response of the system to perturbations could provide such an early warning system.
Models such as that developed by Garcia Lorenzana and collaborators remain stylized and don’t aim to make quantitative predictions for a particular ecosystem in a particular place. Instead, this fundamental research has the goal of identifying mechanisms that lead to the stability of complex ecosystems: the “devious strategies” May was asking about 50 years ago. However, researchers have already taken some steps to make these modeling approaches relevant to real-world situations. For example, researchers have used experiments with bacterial communities to test an analytical theory for a multispecies system, showing that the theory could reliably predict the dynamics of species abundances [9].
Garcia Lorenzana and collaborators’ work is not only of interest to ecologists but also demonstrates how looking at questions outside of physics can enrich physics itself. Specifically, they show that their metacommunity model is described by a field theory that enhances directed percolation by including memory, or non-Markovian, effects, as well as colored noise (noise with more complex spectral features than white noise). The researchers suggest that it would be interesting to further investigate this theory and the types of transitions it produces. Such studies could indeed lead to discoveries of new forms of behavior in complex systems. It would not be the first time that work inspired by a problem in another discipline opens up new avenues within physics itself.
References
- D. Stauffer, “Introduction to statistical physics outside physics,” Phys. A 336, 1 (2004).
- D. Helbing and A. Johansson, “Pedestrian, crowd and evacuation dynamics,” in Encyclopedia of Complexity and Systems Science, edited by R. Meyers (Springer, New York, 2009)[Amazon][WorldCat].
- J. Doyne Farmer, “Making Sense of Chaos: A Better Economics for a Better World,” (Yale University Press, New Haven, 2024)[Amazon][WorldCat].
- R. Conte et al., “Manifesto of computational social science,” Eur. Phys. J.: Spec. Top. 214, 325 (2012).
- G. Garcia Lorenzana et al., “Interactions and migration rescuing ecological diversity,” PRX Life 2, 013014 (2024).
- S. Allesina and S. Tang, “The stability–complexity relationship at age 40: A random matrix perspective,” Population Ecology 57, 63 (2015).
- R. M. May, “Will a large complex system be stable?” Nature 238, 413 (1972).
- K. A. Takeuchi et al., “Directed percolation criticality in turbulent liquid crystals,” Phys. Rev. Lett. 99, 234503 (2007).
- J. Hu et al., “Emergent phases of ecological diversity and dynamics mapped in microcosms,” Science 378, 85 (2022).