Nobel Prize: Mimicking Human Intelligence with Neural Networks
This story will be updated with a longer explanation of the Nobel-winning work on Thursday, 10 October.
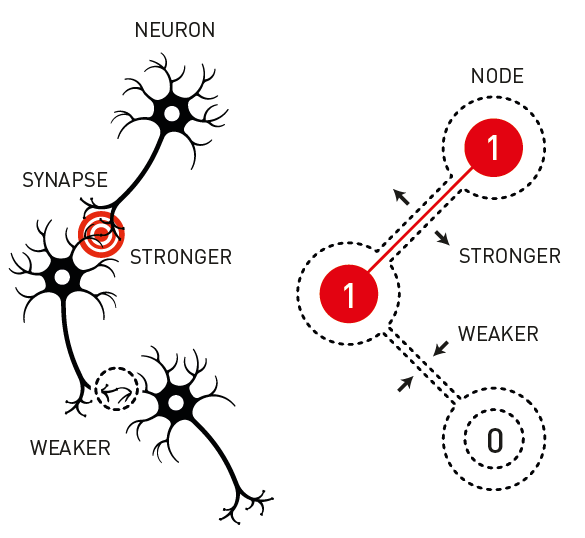
Certain processes in the brain, such as recognition and classification, can be modeled as interactions of artificial neurons, or “nodes,” in a highly interconnected network. This physics-inspired approach to human learning has been recognized with the 2024 Nobel Prize in Physics. John Hopfield from Princeton University and Geoffrey Hinton from the University of Toronto share this year’s prize for their work on artificial neural networks, which have become the basis of many artificial intelligence technologies, such as facial recognition and chatbots.
An artificial neural network is a collection of nodes, each of which has a value that depends on the values of the nodes to which it’s connected. In the early 1980s, Hopfield showed that these networks can be imprinted with a kind of memory that can recognize images through an energy-minimization process. Building on that work, Hinton showed how the couplings between nodes could be tuned (or “trained”) to perform specific tasks, such as data sorting and classification. Together, the contributions of these physicists set the stage for the machine-learning revolution taking hold in the world today.
—Michael Schirber
Michael Schirber is a Corresponding Editor for Physics Magazine based in Lyon, France.