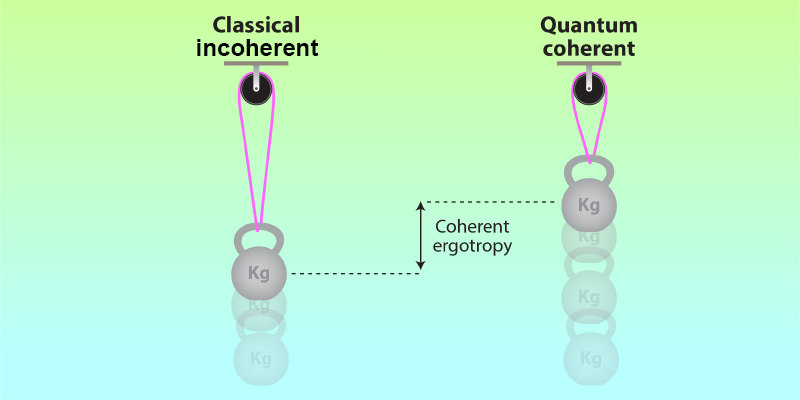
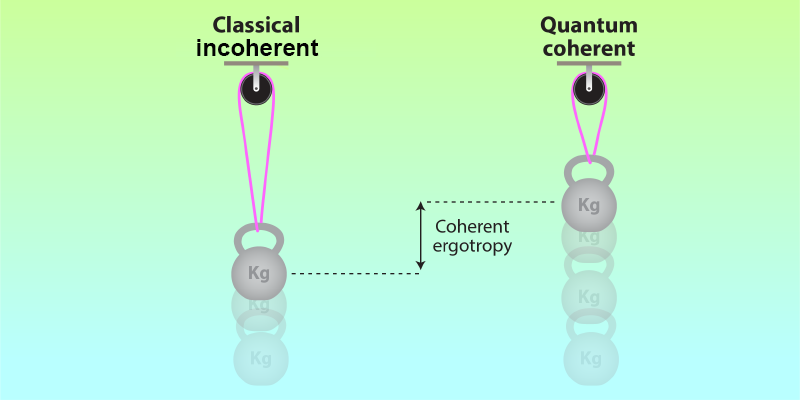
Quantum Coherence Boosts Quantum Work
The history of thermodynamics is intimately linked to the development of heat engines and the production of mechanical work. Determining the maximum amount of work that can be extracted from a given system is thus a central problem of classical thermodynamics and, in more recent years, of quantum thermodynamics. In quantum systems, coherence, which is related to linear superposition of states, is expected to enhance the work capacity. Now Zhibo Niu and colleagues from the University of Science and Technology of China have experimentally verified this theoretical prediction, hence confirming that quantum coherence is a potentially useful resource for nanodevice engineering [1] (Fig. 1).
A distinctive feature of quantum mechanics is that systems can be prepared in coherent superpositions of different states. This fundamental property is at the origin of quantum interference effects. It has also been identified as a crucial physical resource in quantum information science, making it possible for quantum algorithms, such as number factorization, to outperform their classical counterparts [2]. Lately, a related question has attracted considerable attention: Can energetic coherence, associated with linear superpositions of energy states, also be a resource in the field of thermodynamics, enabling the extraction of more work than classically possible [3]?
The amount of energy that can be gained from a quantum system is, rather surprisingly, not given by the energy of the system. The physical origin of this counterintuitive fact is that the second law of thermodynamics, in the formulation of Kelvin and Planck, prevents the cyclic extraction of work from thermal equilibrium states [4]. Thermal states are for this reason often called passive [5]. The maximum amount of work than can extracted in a cyclic (unitary) process is thus given by the “nonpassive” part of their average energy. This quantity, defined as the difference between the mean energy of the state and the corresponding passive state, was given the name ergotropy (from “ergo” for work and “trope” for transformation), in analogy with the word entropy [6]. In systems without coherence, the incoherent ergotropy depends only on the population distribution of energy levels. However, a new nonclassical contribution, the coherent ergotropy, appears in the presence of coherence between energy levels [7]. Remarkably, it is non-negative, indicating that coherence can enhance the work production capacity of the system.
For their investigation, Niu and colleagues turned to the solid-state qubit formed by the single electron spin of a nitrogen-vacancy center in a diamond crystal. Such systems offer excellent control of their states and exhibit very long spin coherence, even at room temperature [8]. Coherent superpositions of states of the qubit were prepared by inducing Rabi oscillations driven by microwave pulses. The average energy of the electron spin was measured by coupling the spin to an ancillary qubit realized by an adjacent nuclear spin. For short evolution times, the average energy of the electron spin could be mapped onto the state of the nuclear spin, and thus read out using laser pulses. The ergotropy of an electron spin state was then evaluated by calculating the difference of the results of two energy measurements: the mean energy of the initial state and the mean energy of the state after work extraction. The total, incoherent, and coherent ergotropies were all determined in the experiment by preparing different system states.
The amount of coherence was characterized with the help of an information-theoretic quantity, called the relative entropy of coherence, which vanishes for a classical state and monotonically increases with growing quantum coherence [9]. By varying the amount of coherence, Niu and colleagues could demonstrate the increase of the coherent ergotropy when the electron qubit is made more coherent, as predicted by theory.
This study with a single qubit provides compelling evidence that coherence is a useful physical resource for extracting more work from a quantum system than would be the case from its classical counterpart. These findings suggest that quantum coherent machines could outperform classical incoherent ones by successfully harnessing coherence. Hints of such an advantage were recently seen in a photonic heat engine made of a cavity with a moving mirror that acts as a piston. The efficiency of the engine was significantly increased, approaching near-unity efficiency, when fueled by a quantum reservoir with coherent superpositions of the energy level of atoms in a superradiant state [10].
Further investigations should examine the extension of these results to a larger number of qubits and to the detrimental influence of environment-induced decoherence. Ultimately, this research could lead to the development of quantum-enhanced nanomachines.
References
- Z. Niu et al., “Experimental investigation of coherent ergotropy in a single spin system,” Phys. Rev. Lett. 133, 180401 (2024).
- M. A. Nielsen and I. L. Chuang, Quantum Computation and Information (Cambridge University Press, Cambridge, 2000)[Amazon][WorldCat].
- S. Deffner and S. Campbell, Quantum Thermodynamics (IOP Publishing, Bristol, 2019)[Amazon][WorldCat].
- A. B. Pippard, Elements of Classical Thermodynamics (Cambridge University Press, Cambridge, 1957)[Amazon][WorldCat].
- W. Pusz and S. L. Woronowicz, “Passive states and KMS states for general quantum systems,” Commun. Math. Phys. 58, 273 (1978).
- A. E Allahverdyan et al., “Maximal work extraction from finite quantum systems,” Europhys. Lett. 67, 565 (2004).
- G. Francica et al., “Quantum coherence and ergotropy,” Phys. Rev. Lett. 125, 180603 (2020).
- M. W. Doherty et al., “The nitrogen-vacancy colour centre in diamond,” Phys. Rep. 528, 1 (2013).
- A. Streltsov et al., “Colloquium: Quantum coherence as a resource,” Rev. Mod. Phys. 89, 041003 (2017).
- J. Kim et al., “A photonic quantum engine driven by superradiance,” Nat. Photonics 16, 707 (2022).