Symmetry Spotted in Statistical Mechanics
Symmetry is a foundational concept in physics, describing properties that remain unchanged under transformations such as rotation and translation. Recognizing these invariances, whether intuitively or through complex mathematics, has been pivotal in developing classical mechanics, the theory of relativity, and quantum mechanics. For example, the celebrated standard model of particle physics is built on such symmetry principles. Now Matthias Schmidt and colleagues at the University of Bayreuth, Germany, have identified a new type of invariance in statistical mechanics (the theoretical framework that connects the collective behavior of particles to their microscopic interactions) [1]. With this discovery, the researchers offer a unifying perspective on subtle relationships between observable properties and provide a general approach for deriving new relations.
The concept of conserved, or time-invariant, properties has roots in ancient philosophy and was crucial to the rise of modern science in the 17th century. Energy conservation became a cornerstone of thermodynamics in the 19th century, when engineers uncovered the link between heat and work. Another important type of invariance is Galilean invariance, which states that the laws of physics are identical in all reference frames moving at a constant velocity relative to each other, resulting in specific relations between positions and velocities in different frames. Its extension, Lorentz invariance, posits that the speed of light is independent of the reference frame. Einstein’s special relativity is based on Lorentz invariance, while his general relativity broadens the idea to all coordinate transformations. These final examples illustrate that invariance not only provides relations between physical observables but can shape our understanding of space, time, and other basic concepts.
In 1918, the mathematician Emmy Noether proved that a conserved quantity is associated with each continuous symmetry of a physical system [2, 3]. For example, conservation of linear or angular momentum reflects invariance under translations or rotations in space, whereas energy conservation reflects invariance under translations in time. This seemingly abstract theorem reshaped how the laws of physics are derived and even how “matter” and “interactions” are defined. For instance, the standard model of particle physics is a quantum field theory based on the concept of gauge invariance, the fact that the laws of physics are unchanged by certain transformations of the variables used to describe the laws. In that case, the relevant symmetries are not as familiar as spatial translations and rotations, but they guided the determination of the corresponding conserved quantities, as prescribed by Noether’s theorem.
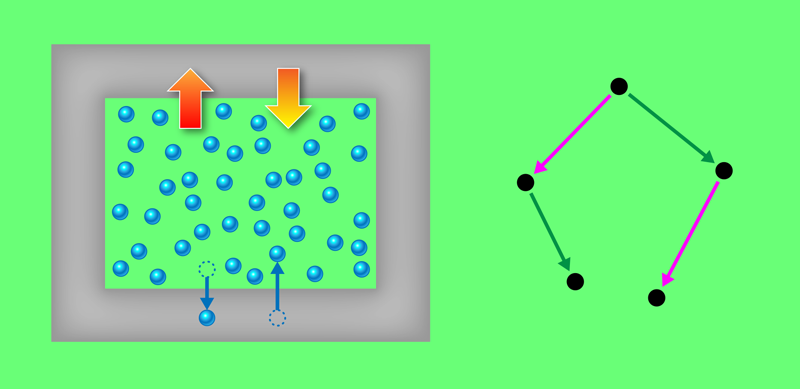
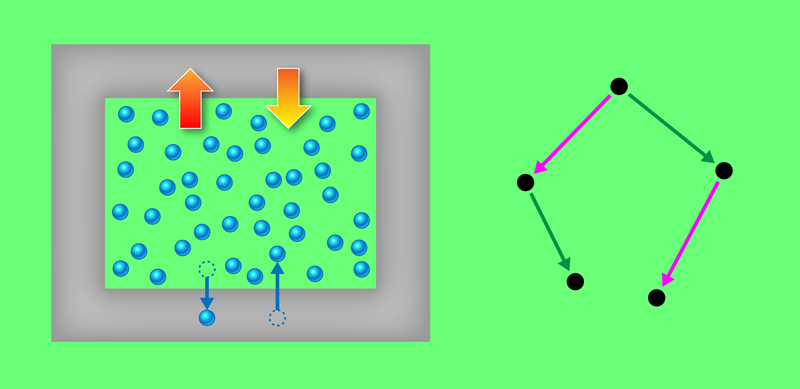
Over the past few years, Schmidt and colleagues have put the power of Noether’s theorem to work to obtain results in the context of equilibrium statistical mechanics [4–6]. This branch of physics deals with the properties of ensembles of microscopic configurations of a classical system. One such ensemble is the grand-canonical ensemble, in which the system retains a constant temperature and chemical potential by exchanging energy and particles with a heat and particle reservoir (Fig. 1, left). Equilibrium statistical mechanics is the relevant conceptual framework for understanding a large system’s collective features, such as its phase diagram and other thermodynamic properties, based on the microscopic interactions of its particles.
In that previous work, Schmidt and colleagues introduced an infinitesimal “phase-space shifting” operation, which transforms the positions and momenta of particles in a specific way (Fig. 1, right). The researchers used this operation and Noether’s theorem to derive exact relations for the correlations between forces present in the system and general observable properties. Such relations can be expressed as averages of phase-space functions. For example, the correlation between the local density of external forces acting on the system and the local density of particles is equal to the gradient of the latter. The researchers coined such identities “hyperforce” relations.
In the current study, Schmidt and colleagues have identified the phase-space-shifting operation as a gauge transformation for microscopic states in equilibrium statistical mechanics. Importantly, this transformation leaves the microstates and all corresponding phase-space functions, including all observable properties, unchanged. Such a gauge invariance provides an elegant and efficient framework for rederiving and verifying hyperforce relations. Crucially, it also delivers a consistent framework for understanding these relations and a systematic way to obtain new ones. The researchers illustrate their results through numerical simulations of a specific system: one-dimensional hard rods confined between two hard walls. In doing so, they show that gauge invariance is also preserved when using a finite, instead of infinitesimal, phase-space-shifting operation.
As noted by Schmidt and colleagues, the role of gauge transformations also resonates with other strategies to compute statistical properties of particle-based systems [7–10]. For example, asking what would change under a slight adjustment of the coordinate system is not so different from asking what would change under a slight movement of the particles. By extension, the change in the probability of certain microscopic states being present, which depends on their energy, is related to the energy change associated with moving particles. In turn, this probability change is correlated with the forces acting on the particles because force is the gradient of energy with respect to particle position.
The researchers’ gauge-invariance framework might lead to new force-based estimators of the local properties of these systems, such as the local particle density or the radial distribution functions quantifying the spatial correlations between particles. Such estimators might require fewer microscopic configurations to achieve a target accuracy, thereby reducing the computational cost and corresponding carbon footprint. Future directions could include analyzing dynamic properties in and out of equilibrium within the statistical mechanics of trajectories, instead of microscopic configurations. Considering gauge invariance in that context would establish a stronger connection between equilibrium statistical mechanics and quantum mechanics. Beyond fundamental work, the relations derived by the researchers, and ones yet to be obtained from the proposed framework, might give rise to new computational tools with applications in all fields in which molecular simulations already play an essential role, from materials science to molecular biology.
References
- J. Müller et al., “Gauge invariance of equilibrium statistical mechanics,” Phys. Rev. Lett. 133, 217101 (2024).
- E. Noether, “Invariante variationsprobleme,” Nachr. Ges. Wiss. Gottingen, Math.-Phys. Kl 235 (1918); [English translation] “Invariant variation problems,” Transp. Theory Stat. Phys. 1, 186 (1971).
- N. Byers, “E. Noether’s discovery of the deep connection between symmetries and conservation laws,” arXiv:physics/9807044.
- S. Hermann and M. Schmidt, “Noether’s theorem in statistical mechanics,” Commun. Phys. 4, 176 (2021).
- S. Hermann and M. Schmidt, “Why Noether’s theorem applies to statistical mechanics,” J. Phys.: Condens. Matt. 34, 213001 (2022).
- S. Robitschko et al., “Hyperforce balance via thermal Noether invariance of any observable,” Commun. Phys. 7, 103 (2024).
- D. Borgis et al., “Computation of pair distribution functions and three-dimensional densities with a reduced variance principle,” Mol. Phys. 111, 3486 (2013).
- D. de las Heras and M. Schmidt, “Better than counting: Density profiles from force sampling,” Phys. Rev. Lett. 120, 218001 (2018).
- B. Rotenberg, “Use the force! Reduced variance estimators for densities, radial distribution functions, and local mobilities in molecular simulations,” J. Chem. Phys. 153, 150902 (2020).
- A. Purohit et al., “Force-sampling methods for density distributions as instances of mapped averaging,” Mol. Phys. 117, 2822 (2019).