Spike Mechanism of Biological Neurons May Boost Artificial Neural Networks
Artificial neural networks (ANNs) have brought about many stunning tools in the past decade, including the Nobel-Prize-winning AlphaFold model for protein-structure prediction [1]. However, this success comes with an ever-increasing economic and environmental cost: Processing the vast amounts of data for training such models on machine-learning tasks requires staggering amounts of energy [2]. As their name suggests, ANNs are computational algorithms that take inspiration from their biological counterparts. Despite some similarity between real and artificial neural networks, biological ones operate with an energy budget many orders of magnitude lower than ANNs. Their secret? Information is relayed among neurons via short electrical pulses, so-called spikes. The fact that information processing occurs through sparse patterns of electrical pulses leads to remarkable energy efficiency. But surprisingly, similar features have not yet been incorporated into mainstream ANNs. While researchers have studied spiking neural networks (SNNs) for decades, the discontinuous nature of spikes implies challenges that complicate the adoption of standard algorithms used to train neural networks. In a new study, Christian Klos and Raoul-Martin Memmesheimer of the University of Bonn, Germany, propose a remarkably simple solution to this problem, derived by taking a deeper look into the spike-generation mechanism of biological neurons [3]. The proposed method could dramatically expand the power of SNNs, which could enable myriad applications in physics, neuroscience, and machine learning.
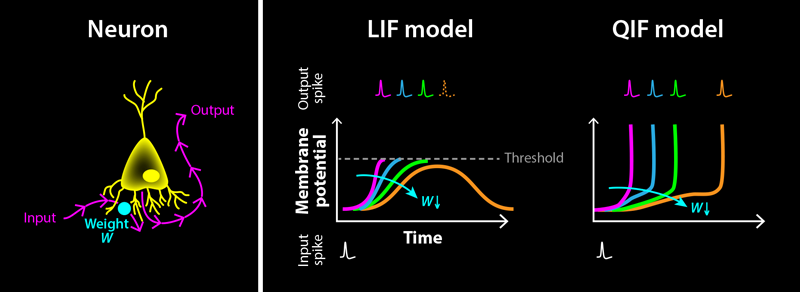
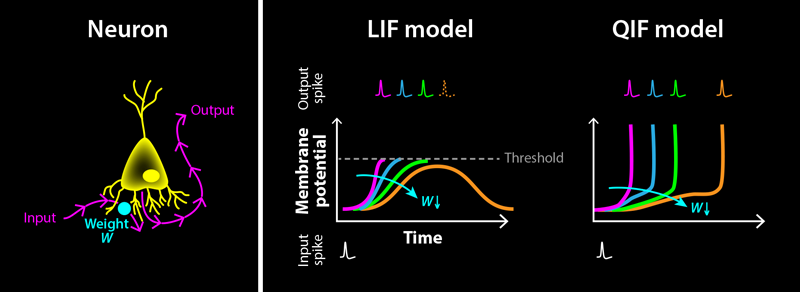
A widely adopted model to describe biological neurons is the “leaky integrate-and-fire” (LIF) model. The LIF model captures a few key properties of biological neurons, is fast to simulate, and can be easily extended to include more complex biological features. Variations of the LIF model have become the standard for studying how SNNs perform on machine-learning tasks [4]. Moreover, the model is found in most neuromorphic hardware systems [5]—computer chips whose architectures take inspiration from the brain to achieve low-power operation.
One of the most relevant variables used in biology to describe neuron activity is the electric potential difference across their cell membrane, known as the membrane potential. In the LIF model, this is represented by a capacitor that is charged through a resistor. The resistor represents ion channels within the cell membrane that allow charged particles to flow in and out of the neuron. Input spikes from other neurons drive currents that charge (or discharge) the capacitor, resulting in a rise (or fall) of the potential, followed by a decay back to the capacitor’s rest value. The strength of this interaction is determined by a scalar quantity called the weight, which is different for each neuron–neuron connection. A neuron itself produces an output spike when its potential exceeds a threshold value. After this output spike, the potential is reset to a subthreshold value. In this type of model, spikes are solely modeled by the time of their occurrence, without accounting for the actual shape of the electrical pulse from a spiking neuron.
Training an SNN boils down to finding, for a given set of input signals, weights that collectively result in desired network responses—that is, temporal patterns of electrical pulses. This process can be illustrated for a simple case: a neuron that receives a single spike from another neuron as an input, connected via an adjustable weight (Fig. 1, left). Starting with a large, positive weight, the input spike results in a sharp rise of the neuron’s potential, hitting the threshold almost immediately and triggering an output spike (Fig. 1, right). By decreasing the weight, this output spike gets shifted to later times. But there is a catch: If the weight becomes too small, the potential never crosses the threshold, leading to an abrupt disappearance of the output spike. Similarly, when increasing the weight again, the output spike reappears abruptly at a finite time. This discontinuous disappearance and reappearance of output spikes is fundamentally incompatible with some of the most widely used training methods for neural networks: gradient-based training algorithms such as error backpropagation [6]. These algorithms assume that continuous changes to a neuron’s weights produce continuous changes in its output. Violating this assumption leads to instabilities that hinder training when using these methods on SNNs. This situation has constituted a major roadblock for SNNs.
In their new work, Klos and Memmesheimer find that only a minor adjustment to the LIF model is required to satisfy the aforementioned continuity property in SNNs: including the characteristic rise–fall shape of spikes on the membrane potential itself. In biological neurons, a spike is a brief, drastic rise and fall of the neuron’s membrane potential. But the LIF model reduces this description to spike timing. Klos and Memmesheimer overcome this simplification by investigating a neuron model that includes such a rise: the quadratic integrate-and-fire (QIF) neuron. This model is almost identical to the LIF model, with one key difference. It contains a nonlinear term designed to self-amplify rises in the membrane potential, which in turn leads to a divergence from the steady state at a finite time (the spike). They show that with this model the output-spike time depends continuously on both weights and input-spike times (Fig. 1, right). Most importantly, instead of disappearing abruptly when the input is too weak, the spike timing smoothly increases to infinity.
To ensure that neurons spike sufficiently often to solve a given computational task, the researchers split a simulation into two periods: a trial period, in which inputs are presented to the SNN and outputs read from it, and a subsequent period in which neuronal dynamics continue, but spiking is facilitated by an additional, steadily increasing input current. The resulting “pseudospikes” can be continuously moved in and out of the trial period during training, providing a smooth mechanism for adjusting the spike activity of SNNs.
Extending previous research on training SNNs using so-called exact error backpropagation [7–9], the present result demonstrates that stable training with gradient-based methods is possible, further closing the gap between SNNs and ANNs while retaining the SNNs’ promise of extremely low power consumption. These results in particular promote the search for novel SNN architectures with output spike times that depend continuously on both inputs and network parameters, a feature that has also been identified as a decisive step in a recent theoretical study [10]. But research will not halt at spikes. I look forward to witnessing what the incorporation of more intricate biological features—such as network heterogeneity, plateau potentials, spike bursts, and extended neuronal structures—will have in store for the future of AI.
References
- J. Jumper et al., “Highly accurate protein structure prediction with AlphaFold,” Nature 596, 583 (2021).
- S. Luccioni et al., “Light bulbs have energy ratings—so why can’t AI chatbots?” Nature 632, 736 (2024).
- C. Klos and R.-M. Memmesheimer, “Smooth exact gradient descent learning in spiking neural networks,” Phys. Rev. Lett. 134, 027301 (2025).
- J. K. Eshraghian et al., “Training spiking neural networks using lessons from deep learning,” Proc. IEEE 111, 1016 (2023).
- C. Frenkel et al., “Bottom-up and top-down approaches for the design of neuromorphic processing systems: Tradeoffs and synergies between natural and artificial intelligence,” Proc. IEEE 111, 623 (2023).
- Y. LeCun et al., “Deep learning,” Nature 521, 436 (2015).
- J. Göltz et al., “Fast and energy-efficient neuromorphic deep learning with first-spike times,” Nat. Mach. Intell. 3, 823 (2021).
- I. M. Comsa et al., “Temporal coding in spiking neural networks with alpha synaptic function,” ICASSP 2020-2020 IEEE Int’l Conf. Acoustics, Speech and Signal Processing (ICASSP) 8529 (2020).
- H. Mostafa, “Supervised learning based on temporal coding in spiking neural networks,” IEEE Trans. Neural Netw. Learning Syst. 29, 3227 (2017).
- M. A. Neuman et al., “Stable learning using spiking neural networks equipped with affine encoders and decoders,” arXiv:2404.04549.