Tireless electrons in mesoscopic gold rings

Yoseph Imry

Viewpoint

Tireless electrons in mesoscopic gold rings

Department of Condensed Matter Physics, Weizmann Institute of Science, Rehovot 76100, Israel

March 30, 2009• Physics 2, 24

The surprising prediction that currents can flow forever in small normal metal rings was confirmed almost twenty years ago. Highly precise new experiments find good agreement with theory that was not seen till now.

Figure caption — **Figure 1:** (Top) This is an artist’s concept, adapted from Ref. [15], showing part of the SQUID assembly—the field and pickup loops hovering over the gold rings of the sample. (Bottom) This figure (Fig. 3(a) from Ref. [9]) presents the difference between the averaged nonlinear responses, induced by the flux and measured by the SQUID, of two rings with sizeable responses, at a range of temperatures vs the applied external flux. Multiple data sets for some temperatures attest to the reproducibility of the results. An approximately fitted sinusoidal curve yields a period which is close to $h / e$ .

It is well known that in a superconductor electrons react strongly to a magnetic field, creating currents that try to shield the flux in the bulk case (the Meissner effect) or cause the flux to be quantized in units of the “two-electron flux quantum,” $Φ_{s} \equiv h / 2 e$ , in a ring-type geometry [1–3]. This flux quantization forms the basis of the SQUID (Superconducting Quantum Interference Device) magnetometer, which consists of a superconducting loop with two weak links and has a maximum supercurrent that is extremely sensitive to the flux through the loop.

The situation for normal electrons on a ring and how they react to a flux through it deserves more thought. The electronic current experiences a finite resistance due, at low temperatures, mainly to defects. It might, therefore, be naively expected to decay on the scale of the relaxation time ( $\sim 10^{- 13}$ s). This is indeed true in the macroscopic limit. It turns out, however, that once the ring is made smaller and reaches the mesoscopic scale (in between the usual micro- and macroscopic ones) and the temperature is low enough, interesting things start to happen. In this quantum coherent realm, electrons do not lose their phase coherence and therefore currents induced by the flux in the ring are persistent and do not decay (as long as the external flux is on). They are an equilibrium property [4,5]. In fact, these persistent currents were first observed in a set of experiments almost two decades ago [6–8], but the magnitude of the currents differed significantly from theoretical predictions. Now, in a new experimental work published in Physical Review Letters [9], Hendrik Bluhm, Nicholas Koshnick, Julie Bert, and Kathryn Moler from Stanford University, and Martin Huber from the University of Colorado, Denver, use a scanning SQUID technique to measure the minute magnetic fields generated by the persistent equilibrium currents flowing in 33 individual mesoscopic ( $1$ – $2 μ m$ diameter) normal metal (Au) rings under an applied magnetic field and find good agreement with theoretical calculations. The SQUID placed over the rings was sensitive enough to measure fluxes down to a fraction of $10^{- 7} Φ_{s}$ .

According to the present theoretical understanding, for noninteracting electrons, persistent currents have a “sample-specific” sign that depends on the detailed defect arrangement in each ring. They are periodic in the flux with a period given by the single-electron flux-unit, $Φ_{0} \equiv h / e$ , and their typical magnitude [10,11] is on the order of $(e /$ $ħ$ ) $E_{c}$ , where the Thouless energy $E_{c} \equiv$ $ħ$ $π^{2} / τ_{D}$ . In the diffusive case (where the circumference $L ≫ ℓ$ , the elastic mean free path), $τ_{D}$ is the diffusion time $L^{2} / D$ of an electron around the ring [11] and $D$ is the diffusion constant ( $D = υ_{F} ℓ / 3 ≅ 0.09 m^{2} / s$ for the samples used [9]). The currents should decrease with increasing temperature $T$ and vanish exponentially for $T ≫ E_{c}$ . The new experimental findings agree better than qualitatively with all aspects of the theory. It is worth noting here that electron-electron interactions are crucial for the current averaged over the ensemble of defect arrangements and this issue will be discussed later.

The measurement of the magnetic response of an individual ring is rather difficult due to the very small signal-to-noise ratio. Ingenious methods for the cancelation of some of the noise, and for the subtraction of the output of the measurement device without the sample have to be devised. This started from the pioneering measurements reported by Chandrasekhar et al. [7] and Mailly et al. [8] in the early 90s and, more recently, Jariwala et al. [12] and Rabaud et al. [13] in 2001. The first measurements on diffusive metallic samples [7] indicated magnitudes of the persistent currents much larger than theoretical predictions. Measurements on semiconducting samples in between the diffusive and ballistic ( $L ≪ ℓ$ ) regimes [8,13] agreed roughly with the theory. The results of later measurements on metallic samples [12] were larger than the theory by a factor of $2$ – $3$ . In the beginning, monolithic arrangements where the SQUID ring was fabricated in situ with the sample were used. This did not enable moving the detector from ring to ring or away from the rings (see Ref. [14]).

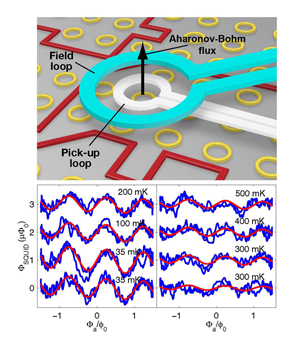
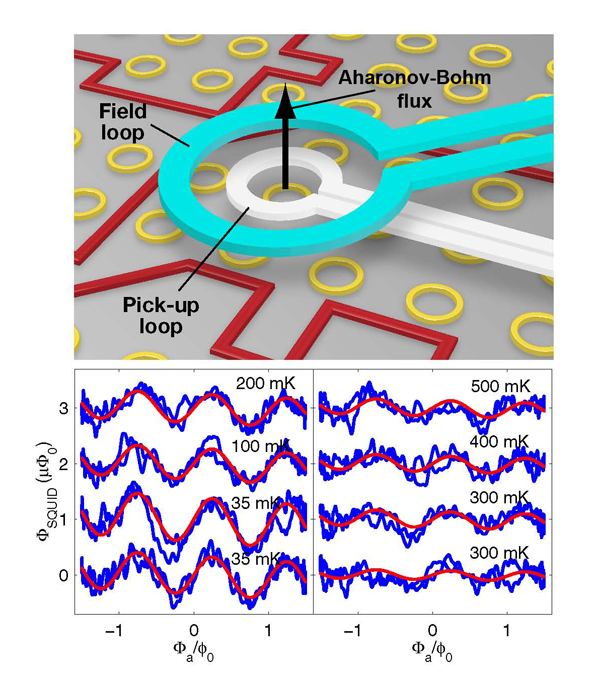
In the newer scanning SQUID technique [15] (see Fig. 1, top) the whole small measurement assembly, consisting of loops creating the applied field and its modulation, the pickup coil of the micro SQUID, and a loop cancelling most of the SQUID response to the applied field, is moving laterally, keeping a fixed small distance from the sample on which a number of gold rings (33 relevant ones for Bluhm et al. [9]) have been laid down. The rings, with diameters ranging from $1$ to $2 μ m$ , were fabricated using a standard electron-beam technique. The response of the sample was dominated by a large linear paramagnetic signal that was approximately 300 times larger than the relevant nonlinear response of the sample, presumably due to magnetic impurities in the substrate. This response varied approximately as $1 / T$ and could be used as a diagnostic for the real temperature of the sample. Low temperatures were achieved with a dilution refrigerator and they were limited by the heating from the external excitation field to the order of $100 mK$ and $20 mK$ for isolated and heatsunk rings. The large background was substantially eliminated by subtracting the response at different points, just above the ring and away from it. Many field sweeps ( $\sim 10^{7}$ ) were averaged out to yield the reported signal. Further consistency checks of the data were applied, an important worry being the variations of the nonlinear sensitivity of the detector with its position relative to the sample.

The mutual induction coefficient between a ring and the SQUID pickup coil was calculated from the geometry. A current of $(e /$ $ħ$ ) $E_{c}$ in the ring should lead to a flux on the order of $10^{- 7} Φ_{0}$ in the pickup loop above it, which is detectable by the measurement device. Results for the flux dependence of the signal consisting of the difference in the response of two suitable rings at temperatures ranging between $35$ and $500 mK$ are shown in Fig.1, bottom.

Before it became feasible to measure persistent current in an individual ring, early experiments used an ensemble of nominally identical rings, for instance, copper rings in Ref. [6], gold rings in Ref. [12], and silver rings in Ref. [16]. For such an ensemble, while the basic $h / e$ –periodic component should average to zero, the $h / 2 e$ “harmonic” in the flux survives. Reference [6] found that the averaged magnitude of the $h / 2 e$ harmonic was also on the order of the Thouless energy, which could not be explained with noninteracting diffusive electrons [In that case, the magnitude of the average current is too small by at least several orders of magnitude.] However, introducing the estimated attractive electron-electron interactions yielded a theoretical result [17] smaller by about a factor of five than experiment [18–20].

Recently, Bary-Soroker et al. [21] (see also a Viewpoint [22] on Ref. [21]) found a possible explanation that may quantitatively account for this discrepancy. Even very clean copper contains on the order of a ppm of magnetic impurities, which are responsible for the relatively large decoherence rate for electrons at low temperatures [23]. Such impurities would suppress superconducting order with a “bare” critical temperature in the $mK$ range. Hence, the strength of the actual attractive interactions in pure copper can be much higher than that obtained from the estimated (in the sub $μ K$ range) superconducting transition temperature of the real metal. It turns out that the energy scale set by pair-breaking magnetic impurity scattering can be large enough to suppress superconductivity but yet smaller than the Thouless energy, to still give a sizeable persistent current. This may happen when the Thouless energy is much larger than the bare transition temperature, which is the case for the samples of Refs. [6,12,16]. Related ideas on the pair-breaking effect of the magnetic field were presented by Schwiete and Oreg [24].

It might be mentioned here that a different approach to studying persistent currents has been developed recently [25]. It employs a cantilever-based torsional magnetometer capable of detecting exceedingly small torques or magnetic moments. Since it does not employ a SQUID, it can also use larger magnetic fields, which would be helpful to see the oscillations of the current in smaller rings.

Novel techniques such as the scanning SQUID [9] and the microtorsional magnetometer [25] enable fresh attacks on the nontrivial and delicate experimental problem of measuring persistent currents in mesoscopic metal rings. Exciting new results for both normal metals and fluctuating superconductors [15,24] on the mesoscale can be expected.

References

B. S. Deaver, Jr., and W. M. Fairbank, Phys. Rev. Lett. 7, 43 (1961); R. Doll and M. Näbauer, 7, 51 (1961)
N. Byers and C. N. Yang, Phys. Rev. Lett. 7, 46 (1961)
F. Bloch, Phys. Rev. Lett. 21, 1241 (1968); Phys. Rev. 166, 415 (1968)
For a quasi-one-dimensional superconductor that has a finite resistance, it was found rather early that the persistent currents do not decay. L. Gunther, and Y. Imry, Solid State Commun. 7, 1391 (1969)
M. Büttiker, Y. Imry, and R. Landauer, Phys. Lett. 96A, 365 (1983)
L. P. Levy, G. Dolan, J. Dunsmuir, and H. Bouchiat, Phys. Rev. Lett. 64, 2074 (1990)
V. Chandrasekhar, R. A. Webb, M. J. Brady, M. B. Ketchen, W. J. Gallagher, and A. Kleinasser, Phys. Rev. Lett. 67, 3578 (1991)
D. Mailly, C. Chapelier, and A. Benoit, Phys. Rev. Lett. 70, 2020 (1993)
H. Bluhm, N. C. Koshnick, J. A. Bert, M. E. Huber, and K. A. Moler, Phys. Rev. Lett. 102, 136802 (2009)
H. F. Cheung, E. K. Riedel, and Y. Gefen, Phys. Rev. Lett. 62, 587 (1989); E. K. Riedel and F. von Oppen, Phys. Rev. B 47, 15449 (1993)
See, for example, Y. Imry, Introduction to Mesoscopic Physics (Oxford University Press, Oxford, 2002)[Amazon][WorldCat]
E. M. Q. Jariwala, P. Mohanty, M. B. Ketchen, and R. A. Webb, Phys. Rev. Lett. 86, 1594 (2001)
W. Rabaud, L. Saminadayar, D. Mailly, K. Hasselbach, A. Benoit, and B. Etienne, Phys. Rev. Lett. 86, 3124 (2001)
Ref. [9] used a gate to disrupt the ring continuity instead
N. C. Koshnick, H. Bluhm, M. E. Huber, and K. A. Moler, Science 318, 1440 (2007)
R. Deblock, R. Bel, B. Reulet, H. Bouchiat, and D. Mailly, Phys. Rev. Lett. 89, 206803 (2002)
The sign of the small flux response is diamagnetic for attractive interactions. This agrees with the tentative determination by Ref. [7], which was more definitively confirmed in Refs. [12,16]
V. Ambegaokar and U. Eckern, Europhys. Lett. 13, 733 (1990)
V. Ambegaokar and U. Eckern, Phys. Rev. Lett. 65, 381 (1990)
These magnitudes are sensitive to the scale-dependence of the interactions
H. Bary-Soroker, O. Entin-Wohlman, Y. Imry, Phys. Rev. Lett. 101, 057001 (2008)
Hélène Bouchiat, Physics 1, 7 (2008)
F. Pierre, A. B. Gougam, A. Anthore, H. Pothier, D. Esteve, and N. O. Birge, Phys. Rev. B 68, 085413 (2003)
G. Schwiete and Y. Oreg, arXiv:0812.4088, considered the pair-breaking effect of the magnetic field
A. C. Bleszynski-Jayich, W. E. Shanks, B. R. Ilic, J. G. E. Harris, J. Vac. Sci. Technol. B 26, 1412 (2008)

About the Author

Yoseph Imry is the Max-Planck Professor of Quantum Physics in the Department of Condensed Matter Physics at the Weizmann Institute of Science. His research interests span much of condensed matter and statistical physics, starting with phase transitions and scaling, superconductivity and Josephson physics and random disordered systems, including electronic ones. He has pioneered the new field of mesoscopic physics, which was the forerunner of much of modern nanoscience. Yoseph Imry is a member of the European Academy of Arts and Sciences (Salzburg), the European Academy of Arts, Sciences and Humanities (Paris), the Israel National Academy of Sciences, and a foreign member of the National Academy of Science of the US. He has received several awards, among which are the Weizmann, Humboldt, Rotschild, Israel, and EMET prizes.