A stimulated atomic response

Dieter Jaksch

Viewpoint

A stimulated atomic response

Clarendon Laboratory, University of Oxford, Parks Road, Oxford OX1 3PU, UK
and Centre for Quantum Technologies, National University of Singapore, Singapore, 117543

April 13, 2009• Physics 2, 29

Inelastic light scattering is used to study correlated phases of one-dimensional Bose gases. This spectroscopic technique can distinguish superfluid and insulating phases and allow identification of the transition from one to the other.

Figure caption — **Figure 1:** One layer of a regular array of independent one-dimensional chains of ultracold bosonic atoms created by an optical lattice. The two Bragg pulses are also displayed (blue and green arrows). The inset shows an atom absorbing a photon from the first laser beam followed by stimulated emission into the second beam. This process transfers momentum $ħ q$ and energy $ħ ν$ to the atom cloud. Spontaneous emission $Γ$ is suppressed by a large detuning $Δ$ from the atomic transition $| g 〉 \leftrightarrow | e 〉$ .

Scattering particles off solids has provided some of the most fundamental insights into the structure of matter. For instance, interference peaks observed in elastic Bragg scattering of x-ray photons established the existence of crystals with well-localized atomic particles arranged in periodic patterns in space. Similarly, inelastic scattering can measure the relation between momentum and energies transferable to these crystals. Such dispersion relations of phonons and electronic band structures have thus been obtained for a wide range of solid-state systems and can in most cases tell us if the material is a metal or an insulator. Now, David Clément, Nicole Fabbri, Leonardo Fallani, Chiara Fort, and Massimo Inguscio at the Physics Department of the University of Florence in Italy report in Physical Review Letters [1] their use of stimulated inelastic scattering of photons to probe a strongly correlated ultracold bosonic gas trapped in a net of interfering laser beams. The laser light creates a periodic lattice potential for the atoms, which thus acquire properties of a crystal. This spatial periodicity leads to Bloch bands of allowed energies for the atomic motion. The authors analyze the ensuing atom dynamics for weak lattices where the atoms tunnel easily between lattice sites and delocalize to form a superfluid. They then quench tunneling by increasing the potential barrier height between the lattice sites. That causes repulsive atom-atom interactions to dominate and localizes the atoms to the lattice sites into a Mott insulating state. This work demonstrates how to experimentally gain detailed insight into the properties of atomic lattice systems and poses new challenges for theorists.

The most common way to probe ultracold atomic gases is to turn off the trapping potential, allow the gas to expand ballistically, and measure the shadow cast by the expanded cloud. The shadow reveals the density distribution in the gas, which is significantly determined by the initial momentum distribution and interactions between the atoms. By suitably manipulating the gas before the expansion, the properties of interest become visible in the expanded cloud. This method has been successful, for example, in demonstrating the matter-wave behavior of Bose-Einstein condensates by observing interference patterns, or to measure the density-density correlations. Also, Bragg spectroscopy of cold atomic gases is based on the same principle. It uses inelastic scattering of photons to subject the atomic system to a periodic perturbation with well-defined and adjustable momentum and frequency. The amount of energy absorbed by the gas is a measure of its response to this perturbation and can be determined by measuring the width of the gas cloud after ballistic expansion. This technique has been used for investigating Bose-Einstein condensates since 1999, first to probe the higher-energy particlelike excitations [2] and later in the same year for measuring low-energy phonons [3]. More recently, this method has also been applied to explore strongly interacting bosonic [4], and fermionic [5] gases. The work by Clément et al. [1] is the first to apply Bragg spectroscopy to an ultracold atomic gas trapped in an optical lattice and to probe its properties from the superfluid into the Mott regime.

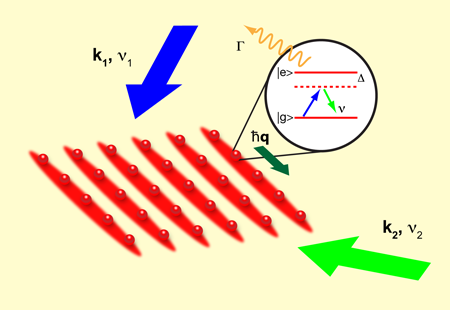
The authors load a three-dimensional Bose-Einstein condensate, which is trapped in a harmonic confining potential, into an optical lattice. With two pairs of counter-propagating laser beams, they create a lattice potential that splits up the condensate into a regular array of cigar-shaped, essentially one-dimensional Bose gases (see Fig. 1). The lattice barriers are sufficiently high that atom tunneling between the one-dimensional gases is negligible and the “cigars” can therefore be considered independent. At the same time, a third lattice is switched on that slices up the one-dimensional gas cigars into regular chains of atoms. This third cigar lattice potential is shallow and tunneling between the sites along the chain is not completely suppressed. Depending on the depth of the cigar potential, the atom chains can either be in the superfluid or Mott insulating regime.

Shortly before suddenly turning off all trapping potentials and allowing the gas to expand the authors apply Bragg pulses. These are two laser pulses that irradiate the atomic sample with photon momenta $ħ k_{1}$ , $ħ k_{2}$ and energies $ħ ν_{1}$ , $ħ ν_{2}$ , respectively. The absorption of a photon from the first laser beam followed by stimulated emission into the second laser beam transfers momentum $ħ q = ħ (k_{1} - k_{2})$ and energy $ħ ν = ħ (ν_{1} - ν_{2})$ to the atomic cloud. This basic process is shown in the inset of Fig. 1. Just like the optical lattice lasers, the Bragg pulses cause an ac Stark shift in the atoms that can be described by adding a conservative potential of the form $V_{B} sin (qx - ν t)$ to the Hamiltonian. This potential is periodic in space $x$ and time $t$ ; its depth $V_{B}$ is determined by laser pulse and atom properties.

The authors check that the measured width $σ$ of the atom cloud after ballistic expansion is proportional to the amount of energy transferred to the atomic sample by the Bragg pulses and that $σ$ increases linearly with the pulse duration and $V_{B}$ . The width $σ$ is thus a measure of the linear response of the atomic system when coupling its density to a perturbation of momentum $ħ q$ and angular frequency $ν$ . This is in contrast to previous work on shaking the lattice [6] where the transferred momentum was not adjustable and the shaking drove the system into the nonlinear regime [7]. The authors adjust the angle of their Bragg pulses so that q is aligned with the longitudinal axes of the atom chains and has a fixed magnitude corresponding to a wavelength 2 $π / | q |$ of about twice the lattice period. They then measure the linear response as a function of the frequency $ν$ . Their study mostly concentrates on excitations inside the lowest Bloch band of the lattice, but they also demonstrate that excitations to higher Bloch bands can be probed with this method.

In the superfluid regime, as the depth of the lattice is increased, the initially broad response of the atom cloud becomes narrower and the peak shifts towards smaller frequencies. This is expected due to the narrowing of the Bloch band with decreasing tunneling between lattice sites, and is qualitatively well explained within mean-field theory. The spectra also show an asymmetry that indicates the presence of a gapped mode in addition to the phonon modes as already theoretically predicted.

When the lattice potential increases, the atom chains enter the Mott insulating regime. The overall magnitude of the response decreases significantly. Simultaneously, the width of the response in the lowest Bloch band increases again and breaks up into several peaks caused by the dominance of the onsite atom-atom interaction over tunneling. The positions of the newly developed peaks do not agree well with predictions for a homogeneous Mott insulator at zero temperature. Furthermore, the system shows a sizable response at low frequencies, below the gap expected for a Mott insulator. The authors attribute these discrepancies to finite temperature and the fact that they are investigating an atomic system that is harmonically trapped instead of a homogeneous one.

In their work Clément et al. have demonstrated that Bragg spectroscopy is a sensitive and precise tool for gaining insight into the physics of strongly correlated atomic lattice gases. In contrast to many other experiments, these results are largely determined by the excitation spectrum of the system. Like all measurement procedures based on ballistic expansion, the method is destructive and does not provide very good spatial resolution, but combining Bragg spectroscopy with other techniques could lead to different insights. For instance, scanning electron microscopy, which is only minimally invasive and yields excellent spatial resolution at the nanometer scale [8], can probe local gas properties in situ. Each of these measurement methods has their virtues and shortcomings. However, one may realistically hope that combining results obtained from them will lead to a complete picture of finite-temperature and dynamical properties of ultracold atomic lattice systems.

References

D. Clément, N. Fabbri, L. Fallani, C. Fort, and M. Inguscio, Phys. Rev. Lett. 102, 155301 (2009)
J. Stenger, S. Inouye, A. P. Chikkatur, D. M. Stamper-Kurn, D. E. Pritchard, and W. Ketterle, Phys. Rev. Lett. 82, 4569 (1999)
D. M. Stamper-Kurn, A. P. Chikkatur, A. Görlitz, S. Inouye, S. Gupta, D. E. Pritchard, and W. Ketterle, Phys. Rev. Lett. 83, 2876 (1999)
S. B. Papp, J. M. Pino, R. J. Wild, S. Ronen, C. E. Wieman, D. S. Jin, and E. A. Cornell, Phys. Rev. Lett. 101, 135301 (2008)
G. Veeravalli, E. Kuhnle, P. Dyke, and C. J. Vale, Phys. Rev. Lett. 101, 250403 (2008)
T. Stöferle, H. Moritz, C. Schori, M. Köhl, and T. Esslinger, Phys. Rev. Lett. 92, 130403 (2004)
S. R. Clark and D. Jaksch, New J. Phys. 8, 160 (2006)
T. Gericke, P. Würtz, D. Reitz, T. Langen, and H. Ott, Nature Physics 4, 949 (2008)

About the Author

Dieter Jaksch obtained his Ph.D. from the University of Innsbruck in Austria in 1999. His research interests are in ultracold atom physics, particularly optical lattices, and their potential applications in quantum simulation and quantum information processing. He is presently a Professor of Physics at the University of Oxford and holds a Visiting Research Professorship at the Center for Quantum Technologies in Singapore. He was named an Outstanding Referee by the American Physical Society in 2008.