Tensor networks—a new tool for old problems

Subir Sachdev

Viewpoint

Tensor networks—a new tool for old problems

Department of Physics, Harvard University, Cambridge, MA 02138, USA

October 26, 2009• Physics 2, 90

A new renormalization group approach that maps lattice problems to tensor networks may hold the key to solving seemingly intractable models of strongly correlated systems in any dimension.

Figure caption — **Figure 1:** Distorted triangular lattice representing the geometry of systems studed experimentally in Ref. [3].

Some of the deepest and most difficult problems in mathematics are also often the simplest to state. The most celebrated example is Fermat’s last theorem, whose statement can be understood by high school students, and yet required the full arsenal of advanced modern mathematics to prove. In condensed matter physics, we are also faced with a difficult class of problems that can be stated quite simply, using language familiar to every beginning student of quantum mechanics. There has been a sustained effort to attack these problems by numerous physicists for over two decades, but there is only partial progress to report. In a recent paper appearing in Physical Review B [1], Zheng-Cheng Gu and Xiao-Gang Wen from the Massachusetts Institute of Technology in the US have developed another promising tool, the so-called “Tensor-Entanglement-Filtering Renormalization approach” with which such problems can be addressed. However, it remains to be seen if it will finally break the log jam and lead to a comprehensive solution.

The simplest of these problems involve only the spin operators $S_{i}$ of electrons residing on the sites, $i$ , of a regular lattice. Each electron can have its spin oriented either up or down, leading to a Hilbert space of $2^{N}$ states, on a lattice of $N$ sites. On this space acts the Hamiltonian

where the $J_{i j}$ are a set of short-range exchange interactions, the strongest of which have $J_{i j} > 0$ , i.e., are antiferromagnetic. We would like to map the ground-state phase diagram of $H$ as a function of the $J_{i j}$ for a variety of lattices in the limit of $N \to \infty$ . Note that we are not interested in obtaining the exact wave function of the ground state: this is a hopeless task in dimensions greater than one. Rather, we would be satisfied in a qualitative characterization of each phase in the space of the $J_{i j}$ . Among the possible phases are (i) a Néel phase, in which the spins have a definite orientation just as in the classical antiferromagnet, with the $〈 S_{i} 〉$ all parallel or antiparallel to each other; (ii) a spiral antiferromagnet, which is magnetically ordered like the Néel phase, but the $〈 S_{i} 〉$ are not collinear; (iii) a valence bond solid (VBS), with the spins paired into $S = 0$ valence bonds, which then crystallize into a preferred arrangement that breaks the lattice symmetry; and (iv) a spin liquid, with no broken symmetries, neutral $S = 1 / 2$ elementary excitations, and varieties of a subtle “topological” order.

For a certain class of $H$ , the above problem has effectively been solved using fast computers. These are lattices for which the Feynman path integral for $H$ can be evaluated as a sum over configurations with positive weights; the sum is then evaluated by sampling based upon the Monte Carlo method. A prominent example of this solution is the recent work by Lou et al. [2] on a set of square-lattice antiferromagnets, in which they find Néel and VBS states.

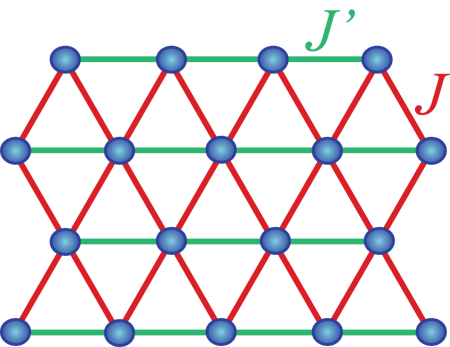
However, there is a large class of lattices for which the path integral does not have any known representation with only positive weights. The Monte Carlo method cannot be used here—this is the famous sign problem. An important example is the model on the triangular lattice, with nearest neighbor couplings $J$ and $J'$ as illustrated in Fig. 1. This model is of experimental importance: the organic insulators $X [Pd (dmit)_{2}]_{2}$ are modeled by a range of values of $J' / J$ as $X$ is varied over a series of monovalent cations [3], and Néel, VBS, and a candidate spin liquid phase have been discovered.

The sign problem has effectively been conquered in one dimension, by the density matrix renormalization group (DMRG) [4]. DMRG carries out a variational optimization over a smartly chosen set of states, the so-called matrix product states (MPS), to represent the ground state with exponential accuracy at only a polynomial cost. In recent years, ideas from quantum information theory have been particularly influential in providing a deeper understanding of the success of DMRG and spawning an intense effort to discover a generalization that works in two and higher dimensions. The ground states of models like $H$ have subsystems with an entanglement entropy that scales with the boundary area (the boundary in one dimension is one lattice site and does not scale with system size, explaining why DMRG works), and methods have been devised that restrict the numerical sampling to only such states. There is an alphabet soup of proposals [5], including MPS, projected entangled-pair states (PEPS), multiscale renormalization ansatz (MERA) [6], tensor renormalization group (TRG) [7], and now the tensor-entanglement-filtering renormalization (TEFR) of Gu and Wen. These methods are connected to each other, and differ mainly in the numerical algorithm used to explore the possible states. So far no previously unsolved model $H$ has been moved into the solved column, although recent results from Evenbly and Vidal [8] show fairly conclusive evidence for VBS order on the kagome lattice, and there is promising progress on frustrated square lattice antiferromagnets [9].

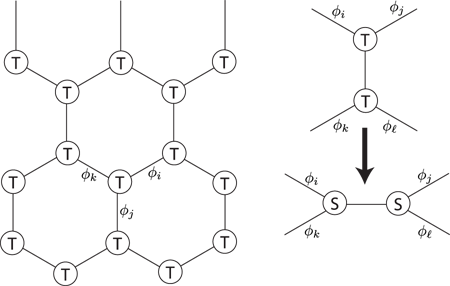
The TEFR descends from the TRG of Levin and Nave [7]. They consider a rewriting of the spacetime partition function of $H$ in terms of a discrete field $ϕ_{i}$ , which resides on the links of a spacetime lattice (not necessarily the same lattice as that of $H$ ). Then, for a very general class of $H$ with local interactions, the partition function can be written as

where $T$ is a tensor on the sites of a spacetime lattice whose components are labeled by the allowed values of the $ϕ_{i}$ . This construction is illustrated in Fig. 2 for the honeycomb lattice, in which case $T$ is a third-rank tensor, as is assumed in Eq. (2). Note that the sum over $ϕ_{i}$ corresponds to a contraction of the tensor indices across each link of the lattice, and $Z$ has all indices contracted (for periodic boundary conditions).

The key step in the TRG is a coarse-graining of Eq. (2) to a more dilute lattice, as in any renormalization group (RG) transformation. In the conventional Wilsonian real-space RG, this is done by just summing over a select subset of the $ϕ_{i}$ . However, the TRG is defined in a way that preserves the virtues of the DMRG in efficiently preserving the local connectivity information for a variety of neighborhood environments. The important step is the transformation illustrated in Fig. 2 in which the tensor $T$ is replaced by a new tensor $S$ with a different local connectivity.

The TEFR is an improvement of the TRG that efficiently removes redundant information on local degrees of freedom that eventually decouple from the long distance behavior, and are not crucial in characterizing the quantum state. This is done by a set of “disentangling” operations during the coarse-graining procedure. The benefit is a nearly one-to-one correspondence between the fixed-point values of the local tensor and the identification of the quantum state. Thus each of the states (i)–(iv) would correspond to distinct values of the fixed-point tensor. In particular, Gu and Wen claim that their method also distinguishes the subtle varieties of topological order in the different spin liquid states.

So far, Gu and Wen have illustrated their method for one-dimensional quantum systems. In these cases, their results are in excellent accord with field-theoretic predictions and the results of DMRG. It remains to be seen if they can break the log jam in two and higher dimensions.

References

Z-C. Gu and X-G. Wen, Phys. Rev. B 80, 155131 (2009)
J. Lou, A. W. Sandvik, and N. Kawashima, arXiv:0908.0740
Y. Shimizu, H. Akimoto, H. Tsujii, A. Tajima, and R. Kato, J. Phys. Condens. Matter 19, 145240 (2007)
S. R. White, Phys. Rev. Lett. 69, 2863 (1992)
J. I. Cirac and F. Verstraete, arXiv:0910.1130
G. Vidal, Phys. Rev. Lett. 99, 220405 (2007)
M. Levin and C. P. Nave, Phys. Rev. Lett. 99, 120601 (2007)
G. Evenbly and G. Vidal, arXiv:0904.3383
V. Murg, F. Verstraete, and J. I. Cirac, Phys. Rev. B 79, 195119 (2009)

About the Author

Subir Sachdev studied at the Indian Institute of Technology in Delhi, the Massachusetts Institute of Technology (MIT), and Harvard University. He is now the Herchel Smith Professor of Physics and department chair of physics at Harvard University. He has been elected to academies of science in the United States and India. Sachdev has received several honors, including the APS LeRoy Apker Award (1983) for his work as an undergraduate at MIT, the APS Lars Onsager Prize (2018), and the Dirac Medal (2018). In 2009 he was recognized as an Outstanding Referee by the American Physical Society.