Implications of old physics simplify the understanding of nuclei

John P. Schiffer

Viewpoint

Implications of old physics simplify the understanding of nuclei

January 4, 2010• Physics 3, 2

Taking into account a tensor force between nucleons in the nucleus provides a more definite description of the average potential experienced by nucleons and the effective residual interaction between them.

Figure caption — **Figure 1:** Schematic illustration of the dependence of the sign of the tensor force between two nucleons on the orientation of the spins relative to the spatial coordinates.

One of the surprises in the history of studying nuclei has been the validity of the shell model, which says that even though nucleons are closely packed, separated by distances that are the same as the range of nuclear forces, they move quasifreely in an average potential. The shell model, originally suggested by Mayer and Jensen to explain the special stability of nuclei with certain “magic numbers” of nucleons, provides a detailed description of the structure of nuclei, including the basis for the emergent collective modes. The parameters that describe the average nuclear potential (and which determine the sequence and energies of the nuclear orbits) are plausibly described in terms of the force between free nucleons, but the details are still somewhat empirical. In a paper appearing in Physical Review Letters, Takaharu Otsuka and colleagues at the University of Tokyo, with collaborators at other institutions in Japan and Norway, explore this connection and the nature of the mean field that arises from all the nucleons [1].

In the past decade, scientists have been able to investigate a wider range of unstable nuclei—especially light unstable nuclei. The data reveal that the energies of the nucleon orbits, the “single-particle states,” shift as nuclei are further from the region of stability. Even the “magic numbers” change in the more exotic nuclei and the gaps between orbits become larger or smaller. A closer look shows that such systematic shifts occur even in stable nuclei and in heavier mass regions.

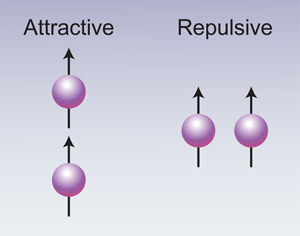
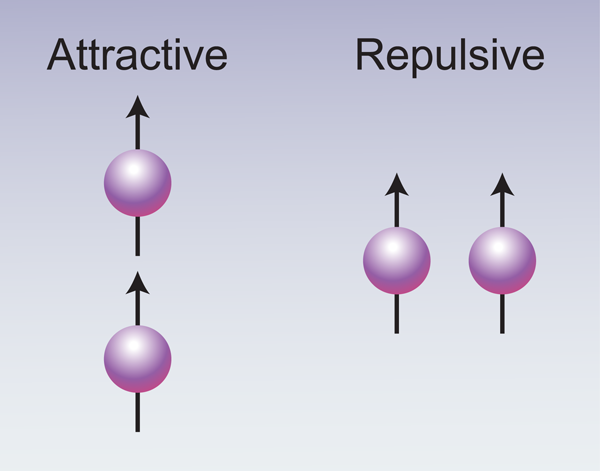
It was Takaharu Otsuka [2] who pointed out that these shifts could be explained by a well-known component of the interaction between free nucleons that depends on the orientation of their spins relative to the direction of the vector connecting them (see Fig. 1). The tensor nature of the interaction arises from the pion-exchange part of the nuclear force. (Pion-exchange is a key feature of the nuclear force, as conceived by Yukawa in 1934, who deduced that the short-range nature of the force must arise from the exchange of a then unknown particle with finite mass and that this force would have a tensor component.) The tensor force acts between two nucleons with their spins aligned, and is attractive when the spins are parallel to the line connecting the nucleons and repulsive when they are perpendicular to this line. This force is the reason, for example, why the proton and neutron have their spins parallel (total angular momentum of $1$ ) in the ground state of the deuteron.

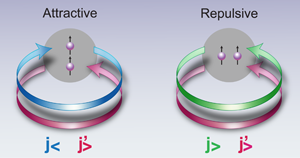
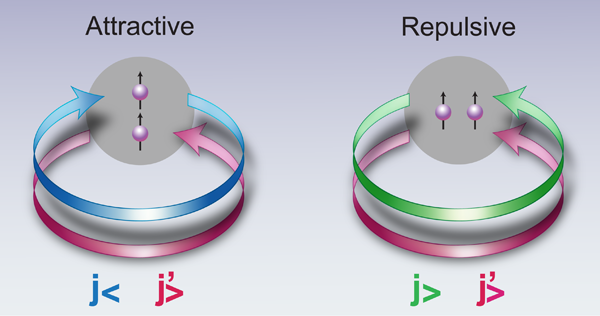
The insight of Otsuka and his collaborators [2] was that this force would still have an overall (monopole) effect that depends only on whether the orbits of the nucleons in the valence states are $j = l + s$ or $j = l - s$ (or “ $j_{>}$ ” and “ $j_{<}$ ” as illustrated in Fig. 2). The point is that the monopole component of the tensor interaction is different depending on whether the nucleon spin is parallel or antiparallel to the direction of its orbital angular momentum, and the monopole component is the average over all possible orientations of nucleons in a given single-particle state. The $j_{>}$ and $j_{<}$ orbits for a given $l$ are paired off and thus there is no tensor contribution for most filled orbits, but near the Fermi surface the pair of orbits are split by the spin-orbit force and the $j_{>}$ orbit fills before the corresponding $j_{<}$ one. Thus as the number of nucleons in an orbit changes in a particular region, the mean field will be altered in such a way that the pattern of single-particle states will change, with gaps disappearing and new ones appearing. This altered pattern is in remarkably good agreement with what is observed experimentally in exotic nuclei, and also reproduces the shifts in the single-particle energies in heavier stable nuclei where data had recently become available over larger regions of neutron excess.

In their current paper, Otsuka and coworkers investigate the effects of the tensor force on the specific residual effective force between the valence nucleons, beyond that represented by the mean field. This force describes a large body of experimental data acquired from nuclear reactions and gamma-ray spectroscopy, especially for the lighter nuclei (below about mass 56). The angle-independent monopole part of the semi-empirical matrix elements of this effective interaction vary considerably for nucleons in different orbits. What Otsuka et al. show is that most of these fluctuations are caused by the tensor force and the magnitude of the tensor force required to explain these fluctuations is very close to that for free nucleons.

These results, in combination with those of Ref. [2], are very promising and may offer a better understanding of the empirical effective interactions that are needed to describe the structure of nuclei. So far only the monopole (angle averaged) interaction has been studied. But the tensor force also predicts a strong dependence on the orientation of orbits that should be apparent in the higher multipole coefficients of the empirical matrix elements. One hopes that these studies can continue and help give more complete insight on the complex question of how the tensor interaction modifies the nuclear force within the nuclear medium.

References

T. Otsuka, T. Suzuki, M. Honma, Y. Utsuno, N. Tsunoda, K. Tsukiyama, and M. Hjorth-Jensen, Phys. Rev. Lett. 104, 012501 (2010)
T. Otsuka et al., Phys. Rev. Lett. 95, 232502 (2005)

About the Author

John Schiffer completed his Ph.D. in 1954 at Yale University, followed by post-doctoral work at The Rice Institute. Since 1956, he has been at Argonne National Laboratory. He also holds a joint appointment at the University of Chicago. He is a fellow of the APS and the AAAS, as well as several other societies, and a recipient of, among others, the Bonner Prize of the APS (1976). He has also been recognized as an Outstanding Referee by the APS. One of his primary interests lies in trying to understand the single-particle structure and effective interactions that underlie the atomic nuclei.