Chiral symmetry breaking and charge order

Jasper van Wezel; Peter Littlewood

Viewpoint

Chiral symmetry breaking and charge order

Cavendish Laboratory, University of Cambridge, Madingley Road, Cambridge CB3 0HE, UK

October 18, 2010• Physics 3, 87

When electronic instabilities give rise to three coexisting density waves, interference between them may lock into a state with helicity.

Figure caption — **Figure 1:** The chiral tetragonal phase of elemental tellurium as a result of multiple charge order. (a) The distortion pattern of a one-dimensional chain with a two-third filled band, described by the displacements $u = cos (q x)$ , with $q = 2 π / 3 a$ . (b) The same one-dimensional pattern repeated throughout a three-dimensional simple cubic lattice. The displacements are given by $u = cos (Q \cdot r) \hat{x}$ , with $Q = (q, q, q)$ and $\hat{x} = (1, 0, 0)$ . (c) The chiral combination of three differently polarized one-dimensional patterns with a relative phase difference of $ϕ = 2 π / 3$ . The distortion pattern $u = (cos (Q \cdot r), cos (Q \cdot r + ϕ), cos (Q \cdot r + 2 ϕ))$ coincides with the tetragonal lattice structure of $Te$ . The chirality of the pattern is indicated by the corkscrewlike arrow following the double bonds in the final structure.

A charge-density wave (CDW) is an ordered state that breaks translational symmetry and is characterized by a modulation in the electronic charge density as well as a corresponding modulation in the spacings of the underlying ionic lattice. It may be formed in a material if there exists a mechanism for transferring electrons from an electronlike part of their Fermi surface to a corresponding holelike part. Such a mechanism may be provided by a variety of energy-lowering interactions, ranging from a direct Fermi surface nesting instability (a Peierls transition [1]) to the lifting of orbital degeneracy (the indirect Jahn Teller effect [2]) and even the formation of local bound states (an excitonic insulator [3]).

A single CDW breaks spatial symmetries in two ways: through the direction of the modulation (its wave vector $Q$ ) and also through its polarization (the direction of the atomic displacements $e$ —see Fig. 1 (b) for an example of a CDW in which $e$ and $Q$ do not align). The combined ionic displacements may also break further symmetries, giving rise to novel phenomena. For example, if inversion symmetry is broken by the displaced lattice, a commensurate CDW is polar (for example $SnTe$ [4]), and an incommensurate CDW may not be pinned by the lattice and become mobile: it can slide in an applied electric field [5]. If there are multiple CDW in the same piece of material, it may happen that the superposition of their modulation patterns either breaks additional symmetries or restores them. For example, the three coexisting CDW in $2H$ - ${TaSe}_{2}$ superpose to reduce the crystal symmetry to orthorhombic, while the original hexagonal symmetry (though still in the presence of the CDW) may be recovered by the application of pressure [6].

It should perhaps have been clear that if a CDW can break inversion symmetry with a polar vector, it could do so with an axial one too—more commonly a helical symmetry. But up till now, such a symmetry breaking transition had not been seen. Using both scanning tunneling microscopy (STM) and optical polarimetry techniques, Junya Ishioka and co-workers from Hokkaido University in Japan have shown that the charge-density wave pattern formed at low temperatures in the layered transition metal dichalcogenide ${TiSe}_{2}$ has a definite chirality [7]. The broken mirror symmetry that is displayed by the chiral structure arises from the combination of three different charge-density waves with a fixed relative phase difference. Because the density waves differ only in the orientation of their in-plane distortions, the spatial charge distribution seen in the STM experiment looks like a corkscrew pattern of charge density, where the orientation of displacements in one layer is continuously rotated into that of the next. The possibility of rotating either clockwise or counterclockwise as one descends into the bulk translates into a breakdown of the bulk rotational symmetry into a twofold chiral symmetry that can be observed in the optical polarimetry experiment as a tendency of the emitted light to be in one of only two preferred polarization states.

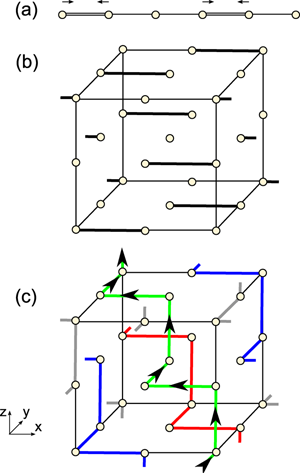
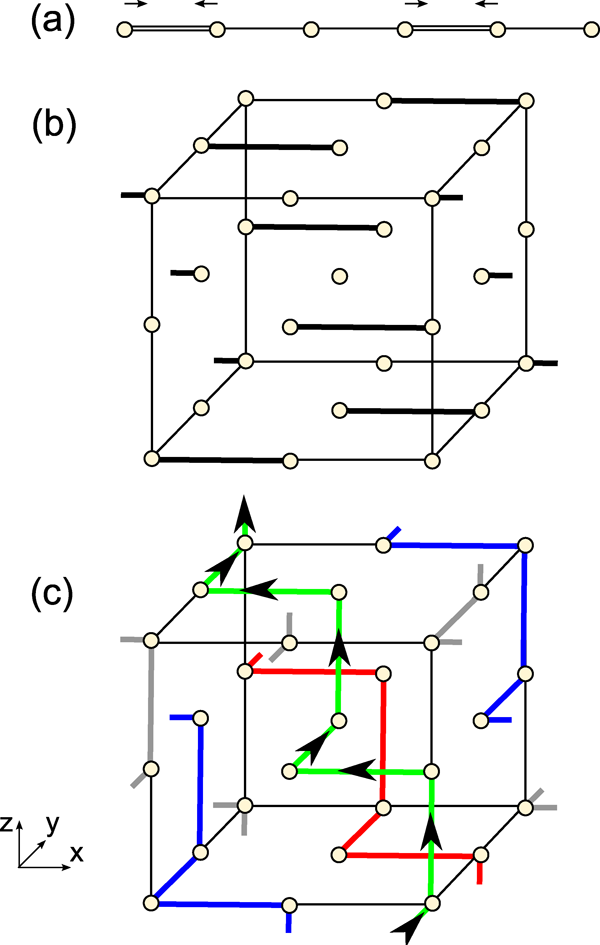
The emergence of chirality from multiple charge-density waves in ${TiSe}_{2}$ can be understood by comparing it to the much simpler case of elemental tellurium. Although $Te$ does not possess a simple cubic phase, its chiral tetragonal lattice structure can be thought of as the result of the simultaneous formation of three charge-density waves in a simple cubic arrangement [8]. (Note that the element $Po$ , just below $Te$ in the periodic table, is the only simple cubic element. The electronic structures of both $Po$ and $Te$ are well described as three perpendicular $p$ -orbital derived bands that are two-thirds full.) All three charge-density waves give rise to the one-dimensional distortion pattern seen in Fig. 1(a). This pattern can be described using, as a modulation of the displacement amplitude, $u = cos (Q \cdot x) \hat{x}$ . Filling the entire cubic lattice this way along charge-density wave vector $Q = (2 π / 3 a, 2 π / 3 a, 2 π / 3 a)$ , gives rise to the arrangement of Fig. 1(b). Adding three such one-dimensional patterns together, with distortions oriented along each of the principal axes of the cubic phase and a relative phase difference of $2 π / 3$ between them, the chiral and tetragonal state of Fig. 1(c) is realized. The relative phase differences are necessary to ensure that no more than two double bonds are formed at each $Te$ site.

Like the $Te$ structure, the chiral phase observed in ${TiSe}_{2}$ by Ishioka and co-workers consists of a combination of three individual charge-density waves, in which the presence of a relative phase difference between them is essential in creating chirality. The ${TiSe}_{2}$ structure differs from that of $Te$ in that its charge-density waves have different ordering vectors $Q_{1, 2, 3}$ , rather than different polarizations of their associated lattice distortions. It also surpasses the tellurium case by having a uniform disordered state available at experimentally accessible temperatures. One can thus observe the formation of CDW order and the locked-in chiral order as the material is cooled through its transition temperature, allowing direct experimental access to this novel phase transition.

Unlike the case of $Te$ , there is no obvious microscopic requirement for the presence of a relative phase difference between the individual charge-density waves in ${TiSe}_{2}$ . It may thus be argued that the chirality of the ${TiSe}_{2}$ pattern is to a large extent “accidental,” in that its existence seems to depend on the detailed microscopic energetics rather than on any overarching physical principle. The importance of such accidental symmetry breaking should not be underestimated. The similar breakdown of inversion symmetry in the charge-density wave transition of materials like ${NbSe}_{3}$ , enables these modes to slide, and gives rise to, for example, dramatic hysteresis effects [9]. In other materials such as $SnTe$ the same breakdown of inversion symmetry in structural phase transitions allows the emergence of a ferroelectric phase [4]. Although the newly discovered pattern in ${TiSe}_{2}$ does not break inversion symmetry and thus does not harbor any sliding charge-density wave or ferroelectric phases, the leftover screw symmetry of the chiral state will be important in understanding the details of its bulk electronic response, as well as the emergence of novel local excitations.

Apart from its new-found chirality, ${TiSe}_{2}$ has also long been in the spotlight because of the enigmatic nature of the force driving its charge-density wave formation. From the outset, explanations in terms of either an (indirect) Jahn-Teller effect or exciton formation have been supported by conflicting experimental results, as well as opposing theoretical interpretations of them [10–13]. The debate was recently revived by the discovery of superconducting phases as the CDW is suppressed upon intercalation with copper or application of pressure [14,15]. The nature of the electron pairing in these superconductors may be expected to be similar to the particle-hole interaction in the parent CDW phase. In light of experiments showing that neither exciton formation nor electron-phonon coupling can be neglected in ${TiSe}_{2}$ , it has very recently been proposed that both phases might be best thought of as being stabilized by a combined process in which the excitons and phonons cooperate to enhance each other’s tendency towards charge order [13,16].

Whether the newly discovered chirality of the charge-density wave in ${TiSe}_{2}$ can assist in determining the precise character of the driving force behind the transition, remains to be seen. To create a three-dimensional chiral pattern in ${TiSe}_{2}$ or related materials like $Te$ , it is essential to have at least three individual CDW instabilities, with nonzero relative phase difference, and non-co-planar displacement patterns. Although the STM data taken by Ishioka and co-workers clearly shows that these conditions are satisfied in ${TiSe}_{2}$ , the microscopic origin of the relative phase differences is not yet clear, and probably depends on the detailed energetics of the interacting excitonic, phononic, orbital, and electronic degrees of freedom. A hint towards an energetic advantage may perhaps be found in the realization that the chiral pattern is dominated by a single CDW in each individual layer, whereas the nonchiral combination without phase differences treats all distortions on an equal footing in each layer.

The discovery that microscopic effects can coincide in such a way as to prefer a chiral combination of the three available charge-density waves in ${TiSe}_{2}$ comes after more than three decades of experimental and theoretical interest in this material. This apparent elusiveness of chiral order without the involvement of magnetic effects opens up room for reexamining many other materials whose charge order is known to involve more than two individual modes. The effect of having the extra chiral degree of freedom added to the properties of such multiple-charge-ordered materials may extend well beyond its direct influence on the polarization of emitted light. The formation of domain walls between regions of different chirality influences the in-plane conductivity, the dominance of a single distortion pattern within each layer allows for the formation of topological defects, and the altered electronic response to polarized light allows for the manipulation of the charge order by addressing its chirality. The “accidental” emergence of chiral order from the combination of multiple charge-density wave instabilities may thus result in a fresh way of looking at this well-known form of electronic order.

References

R. E. Peierls, Quantum Theory of Solids (Oxford University Press, Oxford, 1955), p.108[Amazon][WorldCat]
H. A. Jahn and E. Teller, Proc. R. Soc. London A 161, 220 (1937)
D. Jérome, T. M. Rice, and W. Kohn, Phys. Rev. 158, 462 (1967)
P. B. Littlewood, CRC Crit. Rev. Solid State Mater. Sci. 11, 229 (1984)
G. Grüner, Density Waves in Solids, (Addison-Wesley, Reading, 1994)[Amazon][WorldCat]
P. B. Littlewood and T. M. Rice, Phys. Rev. Lett. 48, 27 (1982)
J. Ishioka, Y. H. Liu, K. Shimatake, T. Kurosawa, K. Ichimura, Y. Toda, M. Oda, and S. Tanda, Phys. Rev. Lett. 105, 176401 (2010)
H. Fukutome, Prog. Theor. Phys. 71, 1 (1984)
N. P. Ong and P. Monceau, Phys. Rev. B 16, 3443 (1977)
A. Zunger and A. J. Freeman, Phys. Rev. B 17, 1839 (1978)
M. Holt, P. Zschack, H. Hong, M. Y. Chou, and T.-C. Chiang, Phys. Rev. Lett. 86, 3799 (2001)
K. Rossnagel, L. Kipp, and M. Skibowski, Phys. Rev. B 65, 235101 (2002)
J. van Wezel, P. Nahai-Williamson, and S. S. Saxena, Phys. Rev. B 81, 165109 (2010)
A. F. Kusmartseva, B. Sipos, H. Berger, L. Forró, and E. Tutiš, Phys. Rev. Lett. 103, 236401, (2009)
E. Morosan, H. W. Zandbergen, B. S. Dennis, J. W. G. Bos, Y. Onose, T. Klimczuk, A. P. Ramirez, N. P. Ong, and R. J. Cava, Nature Phys. 2, 544 (2006)
J. van Wezel, P. Nahai-Williamson, and S. S. Saxena, Europhys. Lett. 89, 47004 (2010)

About the Authors

Jasper van Wezel holds the Aneesur Rahman postdoctoral fellowship at Argonne National Laboratory. He previously worked at the University of Cambridge as a Junior Research Fellow. His research interests include charge-density wave materials, quantum criticality, and other areas of correlated electron physics. He has also worked on applications of condensed matter theory in quantum information processing and related areas of quantum physics.

Peter Littlewood is a professor of physics at the University of Chicago. He was previously director of Argonne National Laboratory, Illinois, and before that a professor of physics and head of the Cavendish Laboratory at the University of Cambridge, UK. His research interests include superconductivity and superfluids, strongly correlated electronic materials, collective dynamics of glasses, density waves in solids, neuroscience, and applications of materials for energy and sustainability.