Non-Abelian anyons: New particles for less than a billion?

Kirill Shtengel

Viewpoint

Non-Abelian anyons: New particles for less than a billion?

Department of Physics and Astronomy, University of California, Riverside, CA 92521, USA

November 1, 2010• Physics 3, 93

The potential discovery of anyons in a fractional quantum Hall device tests the limits of what is known about particles confined to two dimensions.

Figure caption — **Figure 1:** The distinct quantum states resulting from particle worldlines in (a) and (b) do not interfere with each other if they follow non-Abelian statistics. (c) Electron micrograph of the interferometric device. (d) Aharonov-Bohm oscillations with sweeping of the gate voltage at filling factor $ν = 5 / 2$ from $e / 4$ and $e / 2$ quasiparticles.

Half a century ago, Richard Feynman famously proclaimed, “There’s plenty of room at the bottom,” while attempting to foresee the developments in what nowadays has become nanoscience and nanotechnology. He also said, “This field…will not tell us much of fundamental physics (in the sense of, ‘What are the strange particles?’) but…it might tell us much of great interest about the strange phenomena that occur in complex situations.” Well, as it turns out, such strange phenomena may, in fact, involve very unusual new particles.

It is well known that a wave function of two identical bosons is symmetric upon their exchange, while it is antisymmetric for two fermions. However, particles confined to two dimensions aren’t limited to obeying the exchange rules of bosons and fermions. In two dimensions, swapping the positions of two particles in a clockwise manner is distinct from doing it counterclockwise. In three or more dimensions, one could continuously deform such trajectories into each other, rendering the two operations identical. Experimentally, when you confine electrons to an atomically thin layer by essentially electrostatic means, the low-energy collective excitations of the system now behave as two-dimensional particles (although the higher-energy excitations are still conventional electrons). In particular, they can act as anyons—particles whose braiding statistics is neither bosonic nor fermionic. Naturally, one has to go to very low temperatures in search of such quasiparticles, and this is exactly the regime in which the fractional quantum Hall effect—the primary “playground” for finding anyons—is observed.

Writing in Physical Review B, Robert Willett and colleagues from Bell Laboratories in the US present experiments that demonstrate the existence of a very special kind of “non-Abelian” anyons [1]. “Conventional” Abelian anyons have been conjectured to exist in a number of fractional quantum Hall states, yet despite several attempts, their braiding statistics have never been established conclusively. The reason they are called Abelian is because the exchange of two such anyons leads to a nontrivial phase acquired by their wave function, and a series of exchanges merely results in multiple phase factors whose order is irrelevant. Unfortunately, the relative simplicity of their statistics is also the reason why they are so difficult to detect experimentally. The problem is that the phase factors may arise from other sources such as the Aharonov-Bohm effect, the dynamical phase, etc. Hence distilling the statistical phase contribution from the overall phase is quite difficult [2].

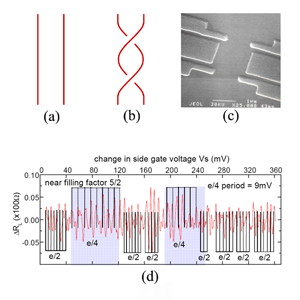
Non-Abelian anyons—the ones that Willett and co-workers are after—are even more interesting objects. A ground state of a system with many such particles must not be unique, with their exchange resulting in mixing of the degenerate states. Formally, this is equivalent to multiplying a vector constructed out of such degenerate ground states by a matrix. Since matrix multiplication is generally noncommutative, the order in which such anyons are exchanged now matters. Surprisingly, the experimental signature of non-Abelian anyons is expected to be much cleaner than that for Abelian anyons. Upon exchange, non-Abelian particles may end up in a different quantum state that will not interfere with their initial state [Fig. 1(a) and (b)]. By contrast with Abelian statistics, whose observation is hinged on extracting the precise phase information from an interference pattern between different particle trajectories, non-Abelian statistics should manifest itself through the suppression of the amplitude of the fringes. Moreover, for certain types of anyons—like those expected to exist in the $ν = 5 / 2$ fractional quantum Hall state [3–5] ( $ν$ being the filling factor) studied by Willett and co-workers—the interference fringes may vanish altogether [6–8]. A specific prediction for the $ν = 5 / 2$ state, dubbed an “even-odd effect,” states that two trajectories of non-Abelian quasiparticles with an electric charge of $e / 4$ should not interfere with one another if there is an odd number of similar quasiparticles encircled by these trajectories; for an even number of encircled quasiparticles the interference pattern should be seen again [7,8]. There are, however, other theories of the $ν = 5 / 2$ state which predict that $e / 4$ particles are Abelian and hence no even-odd effect should occur.

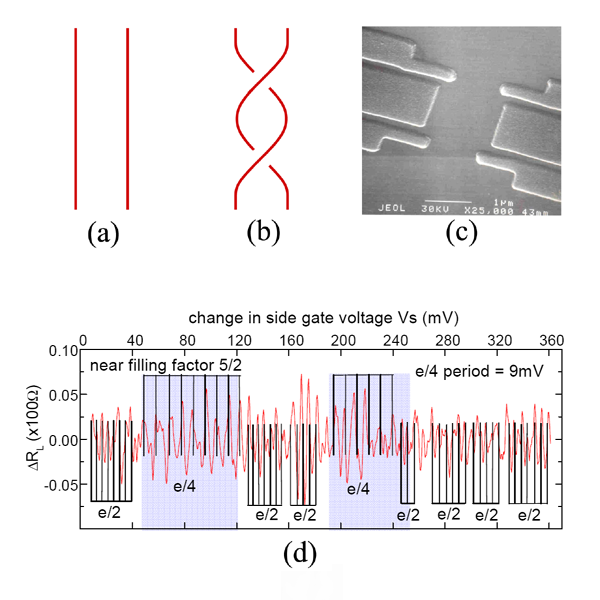
Therefore, a careful interferometric study is needed to confirm the non-Abelian nature of these excitations and precisely such an attempt has been made by Willett et al. [1]. Their main finding is an aperiodic alternating pattern of Aharonov-Bohm oscillations with frequencies corresponding to the quasiparticle charges of $e / 4$ and $e / 2$ . This observation is consistent with the non-Abelian nature of the $e / 4$ excitations; the idea is that by using a gate voltage to change the area inside the interferometer [Fig. 1(c)], one can alternate between even and odd numbers of enclosed $e / 4$ particles. According to the prediction, this should repeatedly turn on and off the interference of $e / 4$ excitations moving along the edge. However, the physics of the quantum Hall edge (which, along with two quantum point contacts, forms an interferometric loop) is more complicated: aside from $e / 4$ anyons, it also supports $e / 2$ excitations whose statistics are Abelian and hence should result in a separate $e / 2$ interference pattern, irrespective of the number of quasiparticles inside the loop. There are no reliable estimates for the relative strength of $e / 4$ vs $e / 2$ tunneling, although some attempts have been made [9,10]. On general grounds, one would expect the $e / 4$ tunneling current to dominate at low temperatures, yet there is a separate important consideration: $e / 2$ quasiparticles are expected to maintain their coherence over longer distances, which would increase their relative contribution to the interference fringes [9,11]. In fact, the latter effect would explain why, at higher temperatures, the interference signal has been found to be completely dominated by the $e / 2$ excitations [12]. At lower temperatures, the interference pattern should then be expected to consist of a sum of ever-present $e / 2$ oscillations and on-and-off $e / 4$ oscillations, rather than display an actual alternation of the two frequencies. The apparent alternation seen by Willett et al. [see Fig. 1(d)] may well be the result of a particular nonuniform way the Fourier transform of the signal has been normalized in this study.

Perhaps the most convincing argument in support of the non-Abelian nature of the observed pattern is the apparent interchange between $e / 4$ and $e / 2$ periods of oscillations when the magnetic field is changed by the amount needed to generate one extra $e / 4$ excitation inside the interferometric loop. Willett et al. have performed a number of important checks, such as the scaling of the oscillation period with the applied magnetic field (for several quantum Hall states), which strongly indicate the Aharonov-Bohm nature of the observed oscillations. The temporal stability of the alternation pattern has also been studied, indicating extremely long life times of the spatial distribution of localized quasiparticles. Together with the earlier study [12], these results make a good case for the existence of non-Abelian anyons in the $ν = 5 / 2$ state, yet it may be too early to declare victory. First and foremost, there is the issue of reproducibility: all published data has so far come from a single sample, albeit subjected to several different preparation cycles. Secondly, the temporal stability of the phase (as opposed to periodicity) of Aharonov-Bohm oscillations needs to be studied, in particular since the non-Abelian explanation comes with its own source of such phase instability. The temperature scaling of the relative strength of $e / 4$ vs $e / 2$ signals might be able to clarify the role of decoherence; this calls for more data at temperatures below $T = 25 mK$ (the lowest temperature for which the data has so far been reported). Hopefully, going to lower temperatures will also result in sharper Fourier transform peaks, making identifying $e / 4$ oscillations more unambiguous.

The work by Willett and collaborators is an indication that the amazing theoretical possibility of non-Abelian anyonic statistics may, in fact, be realized in the $ν = 5 / 2$ fractional quantum Hall state. One hopes that follow-up experiments will be able to unambiguously answer Feynman’s question “What are the strange particles?” in the context of these solid-state systems. The consequences for our understanding of nature, and perhaps even new technological advances [13,14] that so far have mostly occupied the minds of theorists, cannot be underestimated.

References

R. L. Willett, L. N. Pfeiffer, and K. W. West, Phys. Rev. B 82, 205301 (2010)
F. E. Camino, W. Zhou, and V. J. Goldman, Phys. Rev. B 72, 075342 (2005)
G. Moore and N. Read, Nucl. Phys. B 360, 362 (1991)
M. Greiter, X. G. Wen, and F. Wilczek, Nucl. Phys. B 374, 567 (1992)
C. Nayak and F. Wilczek, Nucl. Phys. B 479, 529 (1996)
E. Fradkin, C. Nayak, A. Tsvelik, and F. Wilczek, Nucl. Phys. B 516, 704 (1998)
A. Stern and B. I. Halperin, Phys. Rev. Lett. 96, 016802 (2006)
P. Bonderson, A. Kitaev, and K. Shtengel, Phys. Rev. Lett. 96, 016803 (2006)
W. Bishara, P. Bonderson, C. Nayak, K. Shtengel, and J. K. Slingerland, Phys. Rev. B 80, 155303 (2009)
H. Chen, Z.-X. Hu, K. Yang, E. H. Rezayi, and X. Wan, Phys. Rev. B 80, 235305 (2009)
X. Wan, Z.-X. Hu, E. H. Rezayi, and K. Yang, Phys. Rev. B 77, 165316 (2008)
R. L. Willett, L. N. Pfeiffer, and K. W. West, Proc. Natl. Acad. Sci. U.S.A. 106, 8853 (2009)
S. Das Sarma, M. Freedman, and C. Nayak, Phys. Rev. Lett. 94, 166802 (2005)
C. Nayak, S. H. Simon, A. Stern, M. Freedman, and S. Das Sarma, Rev. Mod. Phys. 80, 1083 (2008)

About the Author

Kirill Shtengel is an Associate Professor at the Department of Physics and Astronomy at the University of California, Riverside. He received his Ph.D. from UCLA in 1999 for his work in statistical mechanics. Following postdoctoral appointments at UC Irvine, Microsoft Research, and Caltech, in 2005 he joined UC Riverside as a faculty member. His current research interests include topological phases of matter and their potential applications for quantum information processing.