Superconducting Qubits Are Getting Serious

Matthias Steffen

Viewpoint

Superconducting Qubits Are Getting Serious

IBM T.J. Watson Research Center, Yorktown Heights, NY 10598, USA

December 5, 2011• Physics 4, 103

When placed inside a 3D electromagnetic cavity, a superconducting qubit can be made potentially more useful because of its large size and long coherence time.

Figure caption — **Figure 1:** Representative evolution of $T_{2}$ coherence times since the first demonstration of a superconducting qubit in 1999 [3]. While the best coherence times (circles, light blue) are longer than those that are reproducible (circles, dark blue), the overall progress has been remarkable as indicated by the dashed black trend line. The most recent 3D work [1] puts another data point right at the top of the list. The dotted green line indicates the coherence time necessary for fault-tolerant quantum computing, assuming the use of quantum error correcting surface codes and a $30 ns$ two-qubit gate.

Bigger is better. Rather interestingly, this mantra appears true for superconducting quantum bits (qubits), which are considered one of the most attractive physical realizations of quantum logic elements for quantum information processing. Reporting in Physical Review Letters, Hanhee Paik, at Yale University, and colleagues demonstrate a novel implementation of a superconducting qubit with dimensions of up to almost $1$ millimeter (about a factor of $10$ – $100$ larger than typically used), exhibiting some of the longest coherence times measured to date [1]. The results carry with them several important messages. First, the results do not just shed light on which decoherence mechanisms play a limiting role for superconducting qubits, but they also show one that does not: Small Josephson junctions apparently do not pose any limit at this stage in the game—contrary to many expectations. Second, superconducting qubits can now be made with coherence times that approach what is necessary for fault-tolerant quantum computing.

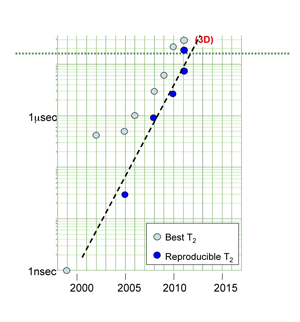
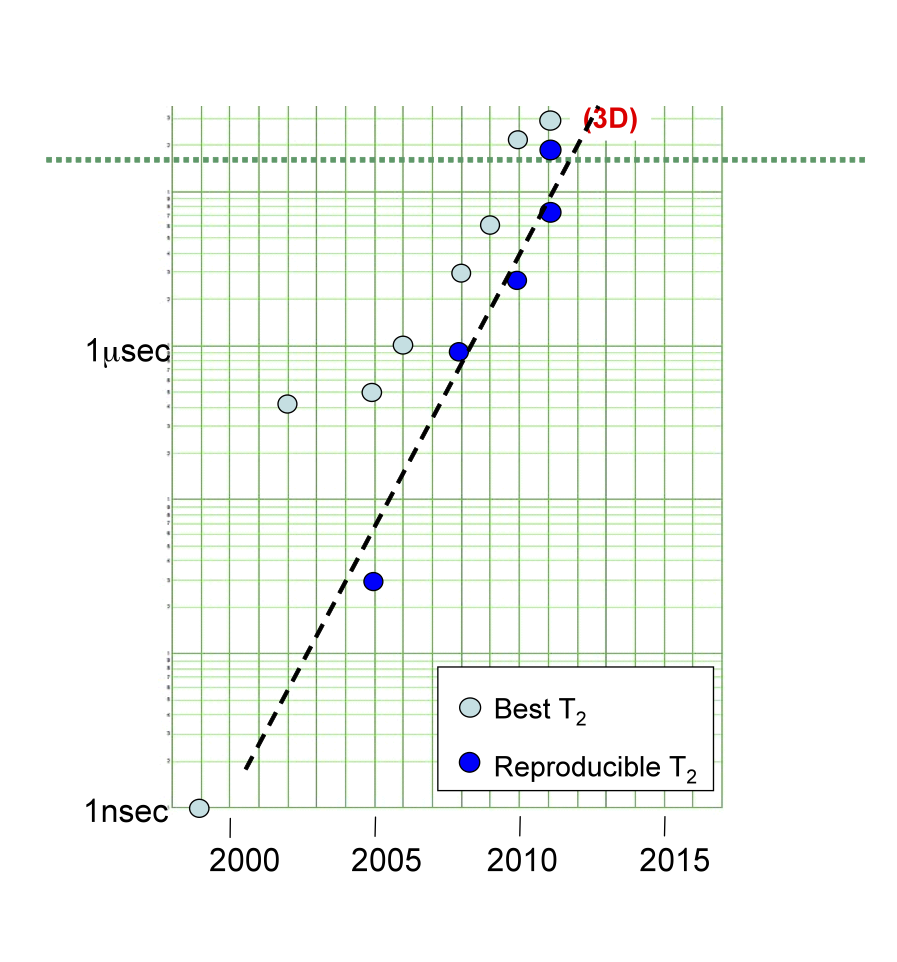
Superconducting qubits are made of inductors, capacitors, and Josephson junctions (JJ) [2], where a JJ consists of a thin layer of insulator between superconducting electrodes. A quantum circuit consisting only of inductors and capacitors gives rise to parabolic energy potentials exhibiting equally spaced energy levels, which are not practical for qubits. The JJ provides the necessary nonlinearity to the system, leading to nonparabolic energy potentials with unequally spaced energy levels such that two out of several energy levels, serving as the qubit states $| 0 〉$ and $| 1 〉$ , can be isolated. The first demonstration of such a qubit in 1999 showed coherent oscillations with coherence times on the order of about $1$ nanosecond ( $ns$ ) [3], more than skeptics had anticipated but far too short for fault tolerant quantum computing, which would require coherence times of at least several tens of microseconds, as discussed a bit later. In the years since, various research groups discovered and reduced the impact of numerous decoherence mechanisms, all of which helped increase coherence times to be reliably near $1$ – $5$ microseconds ( $μ s$ ) (see, for example, Refs. [4–6] and references therein). This represents a factor of over $1000$ improvement in just $10$ years! This progress is also illustrated in Fig. 1.

One of the significant contributors to decoherence is dielectric loss [7]. It has been suspected that dielectric loss at device interfaces (metal/air, metal/substrate) plays a limiting role. Because the interface thickness stays constant even as the overall device is physically made larger the impact of the surface loss can be reduced. The recent work at Yale University [1] takes this to the extreme, where the team fabricated a shunting capacitor $10$ – $100$ times physically larger than conventionally used. In order to prevent such a large qubit from radiating energy away like an antenna, which would lead to decoherence, it is placed inside a three-dimensional waveguide cavity. Typically, the qubit interacts with the lowest frequency mode of the cavity, which is necessary to manipulate and read out the qubit. A three-dimensional waveguide cavity also has a well-defined, reduced electromagnetic mode density in frequency compared with two-dimensional resonators on a chip, which have generally been used thus far for superconducting qubits. This helps reduce unwanted coupling to higher modes, which could reduce decoherence times. The resulting device now exhibits energy relaxation times of up to $T_{1} = 60 μ s$ and dephasing times $T_{2} = 20 μ s$ , which is yet another factor of $20$ – $60$ improvement in coherence times over state-of-the-art.

To what extent any particular loss mechanism has been reduced the most is not clear. The fact is that this implementation of superconducting qubits gives reliable long-lived qubits. The implications that arise from this work are deep and profound. The results show that coherence times of superconducting qubits are not limited by losses in the ultrasmall JJ, at least up to about $60 μ s$ . It is speculated that even the current limit is not due to the JJ but likely other sources of decoherence that will need to be understood. Finally, measured coherence times are now getting close to reaching what is necessary for fault tolerant quantum computing using recently developed quantum error correction schemes [8], assuming realistic two-qubit interaction times near $30$ – $100 ns$ . Of course, the goal is to exceed the threshold to reduce the overhead associated with error correction. By how much is still a question that needs more concrete answers. But even if the field must exceed this number by a factor of $10$ or even $100$ , this does not appear so scary. Recall that the latest result is an improvement over the first results from 1999 by a factor of about $60, 000$ !

Indeed, the field of superconducting qubits has come a long way and fundamental roadblocks still have not appeared. The waveguide cavity approach described by Paik et al. [1] has a promising future ahead and at the bare minimum will continue to play a key role in identifying further decoherence mechanisms. Furthermore, owing to its straightforward implementation, we can expect more groups to enter this research direction over the coming months, with further improvements in device performance. Despite the large feature size of the waveguide cavities, a system consisting of a thousand or more qubits should be accessible without stretching the imagination too much.

None of the results are equivalent to saying that a quantum computer is near. However, it does mean that the field will likely begin to focus on grander engineering challenges while continuing to push the envelope as far as coherence times are concerned. The question is no longer about seeing some two- or three-qubit interaction. The question is how do we begin to package all of this together to make a quantum computer? How do we efficiently couple many qubits together and read them out? What interesting and relevant problems can be solved with a small number of qubits ( $10$ – $100$ )? While answers to these questions will take more time and different resources than the field is used to, one thing is for sure: Unanticipated developments, such as this 3D qubit result, will undoubtedly continue to emerge from this ever-evolving and exciting field of superconducting qubits, continuing the trend shown in Fig. 1.

References

H. Paik, D. I. Schuster, L. S. Bishop, G. Kirchmair, G. Catelani, A. P. Sears, B. R. Johnson, M. J. Reagor, L. Frunzio, L. I. Glazman, S. M. Girvin, M. H. Devoret, and R. J. Schoelkopf, Phys. Rev. Lett. 107, 240501 (2011)
B. D. Josephson, Rev. Mod. Phys. 46, 251 (1974)
Y. Nakamura, Y. A. Pashkin, and J. S. Tsai, Nature 398, 786 (1999)
L. DiCarlo et al., Nature 460, 240 (2009)
I. Chiorescu et al., Science 299, 1869 (2003)
A. D. Corcoles et al., Appl. Phys. Lett. 99, 181906 (2011)
J. M. Martinis et al., Phys. Rev. Lett. 95, 210503 (2005)
R. Raussendorf and J. Harrington, Phys. Rev. Lett. 98, 190504 (2007)

About the Author

Matthias Steffen is manager of the Experimental Quantum Computing team at IBM T.J. Watson’s Research facility in Yorktown Heights. He received his Ph.D. degree in electrical engineering from Stanford University in 2003. After a postdoc at NIST in Boulder, Colorado, and University of California, Santa Barbara, he joined IBM in 2006 and since 2010 manages the quantum computing team. His research career has focused on experimental realizations of quantum bits applicable for quantum information processing, including liquid state NMR and superconducting qubits.

Observation of High Coherence in Josephson Junction Qubits Measured in a Three-Dimensional Circuit QED Architecture

Hanhee Paik, D. I. Schuster, Lev S. Bishop, G. Kirchmair, G. Catelani, A. P. Sears, B. R. Johnson, M. J. Reagor, L. Frunzio, L. I. Glazman, S. M. Girvin, M. H. Devoret, and R. J. Schoelkopf

Phys. Rev. Lett. 107, 240501 (2011)

Published December 5, 2011

Read PDF