Generation of ultrabright biphotons made easy

Valdas Pasiskevicius

Viewpoint

Generation of ultrabright biphotons made easy

Valdas Pasiskevicius

Department of Applied Physics, Royal Institute of Technology, KTH, Stockholm, Sweden

June 20, 2011• Physics 4, 50

A new method to generate ultrabright single-mode biphotons using a backward-wave parametric oscillator is proposed.

Figure caption — **Figure 1:** The solid (dashed) curve represents the spectral power density of the backward- (forward-) wave spontaneous parametric down-conversion at the signal frequency. The vertical (red) lines denote the signal frequencies of adjacent mode pairs of a resonant cavity. The central vertical line is taken at the degenerate frequency.

Since the first proposal of quantum information processing schemes using solely linear optical components [1], it became apparent that such schemes, which are in fact massive interferometers, must rely on spectrally narrowband single-photon sources in order to be efficient. Alternative, resource-efficient, linear schemes were later introduced [2] that aimed to alleviate the requirement of sustaining the stability of the optical setup within a fraction of the photon wavelength; instead, the schemes require stability within the photon coherence time, defined as the Glauber (or intensity) correlation time. Single-photon sources with high spectral brightness and with spectral bandwidth smaller than the natural linewidth are of great interest for efficient photon interaction with cold atoms. Obviously, the tunability of such sources would be of great benefit for cold atom experiments targeting specific resonances.

Biphoton wave packets, containing two strictly correlated photons, are extensively used for entanglement experiments, imaging, and quantum optical communications. Biphotons are generally produced by splitting a single pump photon into “signal” and “idler” photons, using a nonlinear optical medium in a process called spontaneous parametric down-conversion. However, the pump pulses and the resulting biphoton wave packet are restricted to subpicosecond correlation times [3]. A dramatic increase in spectral brightness of a biphoton wave packet was recently demonstrated using continuous-wave-pumped forward-wave parametric down-conversion in a cavity resonant for both the signal and the idler [4]. The doubly resonant cavity design entails rather elaborate stabilization arrangements for reliable device operation. In a paper published in Physical Review A, Chih-Sung Chuu and Stephen E. Harris from Stanford University propose a new method of single-mode biphoton generation with a long correlation length and a correspondingly narrow spectral width [5].

Essential in the proposal is the use of a backward-wave parametric process within a resonant cavity. In the backward-wave parametric process, the pump photon is split into signal and idler photons propagating in opposite directions. Above a certain pumping intensity, this process reaches an instability threshold and self-established oscillation begins. Such a device, called a mirrorless optical parametric oscillator, has been experimentally realized in a periodically poled (a layered structure with alternating orientation) ${KTiOPO}_{4}$ nonlinear crystal [6]. In order to ensure generation of single-biphoton wave packets one has to consider pumping intensities below this self-established oscillation threshold. The choice of the backward-wave parametric process over the forward-wave process for high spectral brightness “signal” and “idler” generation becomes obvious if we compare the spectral width of the parametric gain for both cases, keeping the nonlinear crystal, pump, and signal and idler photon frequencies the same. From the photon momentum conservation condition it is straightforward to show that for a monochromatic pump source, the ratio of the spectral gain widths for the forward-wave and backward-wave parametric processes will be equal to $(ν_{s}^{- 1} + ν_{i}^{- 1}) / | ν_{s}^{- 1} - ν_{i}^{- 1} |$ , where $ν_{s}$ and $ν_{i}$ are the signal and idler group velocities, respectively.

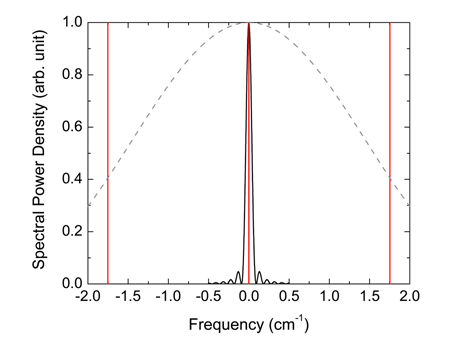
For the degenerate parametric processes in ${KTiOPO}_{4}$ nonlinear crystal pumped by a single-longitudinal mode laser at a wavelength of $532 nm$ , this ratio would be as large as $38$ . The difference in the forward-wave and backward-wave parametric gain spectra is vividly illustrated in Fig. 1. For a $3$ - $cm$ -long ${KTiOPO}_{4}$ crystal, the full width at half maximum of the backward-wave parametric gain is only $2.4 GHz$ . Now consider that there is a resonant cavity around this $3$ - $cm$ -long crystal. Such a doubly resonant cavity will have slightly different longitudinal mode separation for the signal and idler due to dispersion in the nonlinear crystal. Therefore one should expect resonances to occur at so-called cluster frequencies, or where there is a coincidence of the signal and idler cavity resonances. Then it is obvious that in order to achieve a single-mode output from such a doubly resonant cavity, the cluster separation should be larger than the parametric gain bandwidth. In Fig. 1 the red vertical lines denote the cluster frequencies. It is clear that if one employs forward-wave parametric interaction, stable single-mode operation would require substantial effort in cavity stabilization and locking, as shown in Ref. [4]. On the other hand, such a cavity employing a backward-wave parametric gain will be inherently single mode (see Fig. 1). Owing to the narrow gain spectrum, the cavity with the backward-wave parametric interaction will satisfy even the stricter requirement normally applied for single-mode lasers, i.e., the requirement that the free spectral range of the cavity should be larger than half of the gain spectral width. For the example considered in Chuu and Harris’ paper, the free spectral width would be about $2.8 GHz$ . This leaves ample margin for robust single-mode operation without elaborate cavity stabilization techniques. The numerical calculations presented in the paper show that for a cavity finesse (ratio of spectral range of a cavity to the bandwidth of its resonances) of $1000$ , readily achievable with current mirror fabrication technology, the spectral width of the biphoton wave packet would be about $2.1 MHz$ , and the corresponding Glauber correlation time then would be about $68 ns$ . This spectral width is smaller than the typical natural linewidth of atomic transitions. For the pump powers of $770 μ W$ used in the numerical example, the expected biphoton count rate is as high as $1.31 \times 10^{5} s^{- 1}$ , giving spectral brightness of about $6.25 \times 10^{4} s^{- 1} {MHz}^{- 1}$ or $8.16 \times 10^{4} s^{- 1} {MHz}^{- 1}$ per $mW$ of pump power. For comparison, this spectral brightness of biphotons generated by backward-wave interaction in the resonant cavity is $80000$ times higher than the one obtained from nonresonant forward-wave interaction, assuming the same nonlinear material, the same crystal length, and the same pump power.

It is interesting to compare the expected performance of this backward-wave parametric oscillator with the previously reported counter-propagating paired-photon source, exploiting slow-light realized using resonantly coupled $^{87} Rb$ atomic transitions [7]. The reported paired-photon generation rate was $1.2 \times 10^{4} s^{- 1}$ , i.e., an order of magnitude smaller than that in the proposed backward-wave parametric oscillator. Moreover, the scheme in Ref. [7] requires two pump lasers precisely tuned to specific atomic transitions. In Ref. [7] the measured biphoton wave packet Glauber correlation time was about $50 ns$ , i.e., comparable to that expected in the proposed source. By definition, the source using resonant atomic transitions is not tunable to any large extent and, apparently, there is a relatively large background of nonpaired photons generated in the output [7]. The backward-wave parametric oscillator avoids both of these limitations. First, the generation of nonpaired photons will not happen due to the nature of the parametric process, and second, the backward-wave oscillator can be readily tuned either by changing the temperature of the nonlinear crystal [6] or by exploiting self-aligned noncollinear interaction [8]. Experimental realization of the proposed backward-wave oscillator would require a ${KTiOPO}_{4}$ crystal that is periodically poled with a periodicity of $873 nm$ over the length of $3 cm$ . Fabricating such a structure is a rather challenging task, but it is achievable using current structuring techniques developed for this ferroelectric material. Therefore we should look forward to the first experimental realization of this novel backward-wave parametric oscillator for ultrabright biphoton generation.

References

E. Knill, R. Laflamme, and G. J. Milburn, Nature 409, 46 (2001)
D. E. Browne and T. Rudolph, Phys. Rev. Lett. 95, 010501 (2005)
J.-W. Pan, M. Daniell, S. Gasparoni, G. Weihs, and A. Zeilinger, Phys. Rev. Lett. 86, 4435 (2001)
M. Scholz, L. Koch, and O. Benson, Phys. Rev. Lett. 102, 063603 (2009)
C-S. Chuu and S. E. Harris, Phys. Rev. A 83, 061803 (2011)
C. Canalias and V. Pasiskevicius, Nature Photon. 1, 459 (2007)
V. Balic, D. A. Braje, P. Kolchin, G. Y. Yin, and S. E. Harris, Phys. Rev. Lett. 94, 183601 (2005)
G. Strömqvist, V. Pasiskevicius, and C. Canalias, Appl. Phys. Lett. 98, 051108 (2011)

About the Author

Valdas Pasiskevicius is Professor of Physics at the Royal Institute of Technology in Stockholm, Sweden. He received his M.Sc. in Physics from Vilnius University, and Ph.D. from the Institute of Semiconductor Physics also in Vilnius, Lithuania. Since 1996 he has worked at the Royal Institute of Technology. His research interests include nonlinear optics, engineered nonlinear optical materials, and backward-wave parametric processes.