Quantum liquids move to a higher dimension
In a quantum spin liquid, the ground state neither has long-range magnetic order nor does it break any spatial symmetry. Quantum fluctuations—analogous to thermal fluctuations in a classical liquid—can destabilize ordered crystalline phases to produce this exotic phase of matter. Quantum spin liquids are of particular interest as they violate conventional wisdom about condensation of matter as one approaches zero temperature, e.g., to a superconducting phase. Since quantum fluctuations increase in strength as the dimensionality of the system is decreased, the search for quantum liquids has largely occurred in dimensions smaller than three.
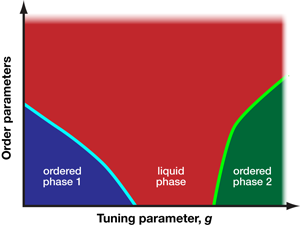
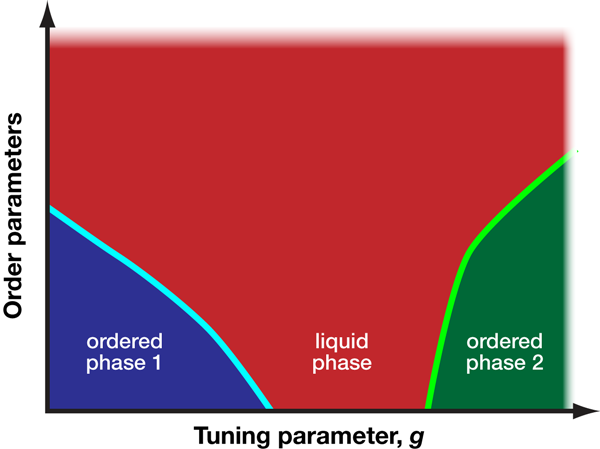
There is ample evidence—quantum Hall edge states [1], for example—for quantum liquid behavior in one spatial dimension, and there are general arguments that show that extended gapless phases—where the energy gap between the ground state and the first excited state vanishes—can emerge in higher dimensions because of quantum criticality, i.e., in parameter regimes where two ordered phases compete to suppress each other (Fig. 1).
Of particular interest is the case of gapless spin liquids. Two classes of gapless spin liquids have been identified, which can be distinguished by the extent of their zero-energy hypersurfaces in reciprocal space [2]: (i) algebraic spin liquids, for which the elementary excitations are not described by free fermions or bosons, and spin correlations have a finite set of singularities at discrete values of momentum; and (ii) spin Bose metals, whose elementary excitations are described by free bosons, with spin correlations that are singular along an extended surface in momentum space. This “Bose surface” is reminiscent of the Fermi surface in conventional metals, except that it can be tuned by parameters of the Hamiltonian, even at fixed particle density. Despite their thorough classification [3], robust examples of extended quantum liquid phases in higher dimensions have been elusive. Much work has been done in constructing examples, such as ring-exchange models [4], but these do not appear to be easy to realize experimentally. This seems to suggest that entropy in nature tends to select ordered states in higher dimensions, even in the presence of strong quantum fluctuations.
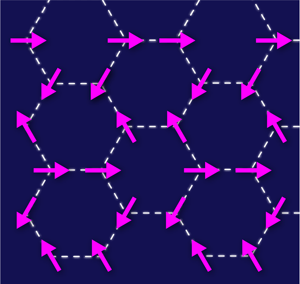
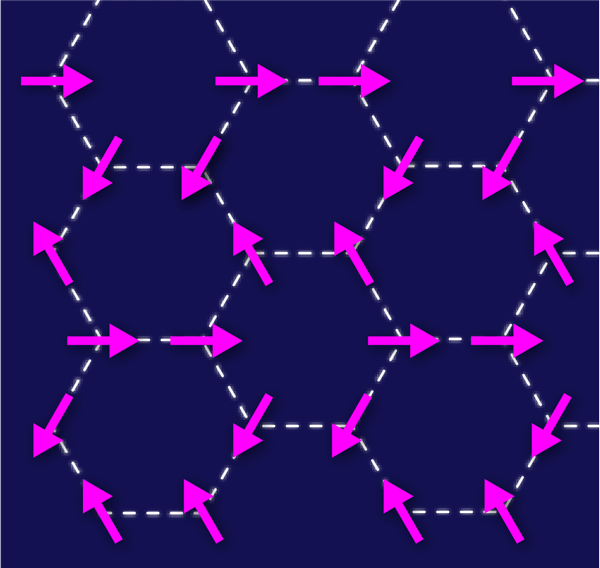
Nonetheless, in a study reported in Physical Review Letters [5], Christopher Varney of the Joint Quantum Institute at the University of Maryland, College Park, and Georgetown University, Washington D.C., and his colleagues present a convincing example of a Bose metal phase in two dimensions. The authors use techniques in numerical diagonalization to examine the zero-temperature phase diagram of the frustrated spin- 1/2 XY model on a honeycomb lattice (see Fig. 2). Monitoring the ground-state fidelity metric, a useful theoretical tool borrowed from quantum information theory [6], and the energy of finite clusters as a function of the competing antiferromagnetic nearest-neighbor and next-nearest-neighbor couplings, the authors identify three quantum phase transitions that separate four phases. The ratio of the competing antiferromagnetic couplings corresponds to the frustration of the system, which here serves as the tuning parameter that governs the phase diagram (akin to the x axis in Fig. 1). Furthermore, the behavior of the condensate fraction in each of the four regimes identifies three of these regimes as ordered phases, corresponding to quantum renormalized versions of classical spin configurations (i.e., where the spins are perturbed, but not destroyed, by quantum fluctuations), while the phase with a vanishing condensate fraction is consistent with a quantum spin liquid [7].
Studying the momentum distribution functions in the ordered phases provides experimentally verifiable evidence for spinon condensation at various points in the Brillouin zone. For example, at small frustration the condensate is a simple antiferromagnet, whereas at very large frustration it corresponds to the collinear spin configuration depicted in Fig. 2. As the spin- 1/2 XY model can be mapped to an equivalent model of hard-core bosons, these ordered phases correspond to Bose condensates at distinct ordering wave vectors. As an interesting aside, Varney et al. noted that in some of the condensates more than one single-particle state is occupied.
The main result of Varney et al.’s study, however, is the finding of an extended quantum spin liquid phase. This regime features a Bose surface with a wave vector that is tunable by the frustration of the model. This particular feature in the momentum distribution function is a defining characteristic of a Bose metal, and would thus serve as a key observation in an experimental study.
The simple XY model, less prone to the singlet formation that would tend to stabilize valence bond order, i.e., a spatially frozen dimer decoration of the underlying lattice, is arguably a better candidate for such quantum spin liquid behavior than the Heisenberg model. Consider, for example, the frustrated Heisenberg model on a square lattice, with competing antiferromagnetic interactions between nearest-neighbor and next-nearest-neighbor spins, a familiar system in condensed matter physics that has been a contender for exhibiting an extended quantum spin liquid regime [8]. The numerical evidence in favor of a gapless quantum spin liquid phase is much less clear cut in this case because of the presence of competing valence bond crystal order, which is difficult to study with available numerical techniques.
The ultimate experimental verification of this Bose metal phase in the spin- 1/2 XY model on a honeycomb lattice will probably hinge on an implementation that uses cold atoms trapped in optical lattices, i.e., relying on a mapping of the spin system to an equivalent model of interacting hard-core bosons. In the past few years, this technology has become a reliable emulation tool for quantum many-body lattice systems with tunable interactions [9]. Bose metal phases are also expected to occur at the interface between superconducting and insulating phases in quasi-two-dimensional films [10]. In this case, disorder in the phase of the superconducting order parameter is expected to lead to a specific type of phase glass that coexists with a bosonic metallic channel. However, it is not yet clear whether there is any connection between the phase glass scenario and the microscopic model studied by Varney et al. Nonetheless, the condensed matter community should be excited to finally have access to a straightforward quantum many-body system that exhibits a Bose metal phase.
References
- B. I. Halperin, P. A. Lee, and N. Read, Phys. Rev. B 47, 7312 (1993)
- O. I. Motrunich and M. P. A. Fisher, Phys. Rev. B 75, 235116 (2007); D. N. Sheng, O. I. Motrunich, and M. P. A. Fisher, 79, 205112 (2009); T. Senthil and P. A. Lee, 71, 174515 (2005)
- X.-G. Wen, Phys. Rev. B 65, 165113 (2002)
- R. G. Melko, A. W. Sandvik, and D. J. Scalapino, Phys. Rev. B 69, 100408 (2004); R. G. Melko and A. W. Sandvik, Phys. Rev. E 72, 026702 (2005); A. Paramekanti, L. Balents, and M. P. A. Fisher, Phys. Rev. B 66, 054526 (2002); L. Balents and A. Paramekanti, 67, 134427 (2003)
- C. N. Varney, K. Sun, V. Galitski, and M. Rigol, Phys. Rev. Lett. 107, 077201 (2011)
- D. F. Abasto, A. Hamma, and P. Zanardi, Phys. Rev. A 78, 010301 (2008)
- S. Sachdev, Quantum Phase Transition, (Cambridge University Press, Cambridge, 2011)[Amazon][WorldCat]
- E. Dagotto and A. Moreo, Phys. Rev. B 39, 4744 (1989); L. Capriotti, F. Becca, A. Parola, and S. Sorella, Phys. Rev. Lett. 87, 097201 (2001); Phys. Rev. B 67, 212402 (2003)
- I. Bloch, J. Dalibard, and W. Zwerger, Rev. Mod. Phys. 80, 885 (2008); M. A. Cazalilla, R. Citro, T. Giamarchi, E. Orignac, and M. Rigol, (to be published); arXiv:1101.5337
- P. Phillips and D. Dalidovich, Science 302, 243 (2003)