Untangling energy metabolism
The study of biology poses a number of exciting challenges, many of which can be addressed with concepts and techniques from physics. Prominent among these is understanding the functioning, and failure, of the networks of nonlinear interactions inside a living cell. In a paper appearing in Physical Review E, Eva Gehrmann at the Darmstadt University of Technology in Germany and her colleagues combine new theoretical approaches to gain insight into the glycolytic pathway, a network of reactions that is essential to the cell’s metabolism [1].
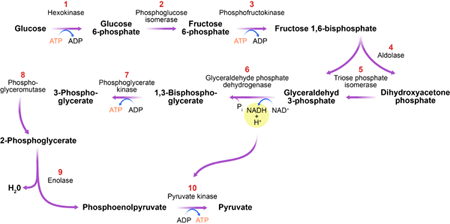
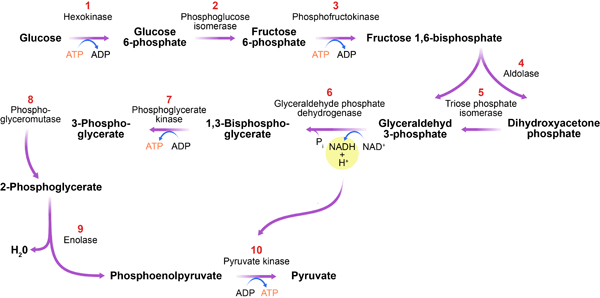
The glycolytic pathway (Fig. 1) is a series of biochemical reactions in which sugar (glucose) is degraded to produce the currency of cellular energy: adenosine triphosphate (ATP). The importance of this process, called glycolysis, can’t be overstated. The glycolytic pathway is found in almost all organisms, highlighting it as one of the most ancient metabolic systems. It catalyzes the key step in the degradation of carbohydrates and, as such, plays a central role in a cell’s energy supply. Furthermore, this process produces essential precursor metabolites for the buildup of biomass.
Glycolysis is also interesting from a theoretical perspective. While many biological systems experience transient oscillations, glycolosis is one of the few (and one of the simplest) natural chemical systems in which sustained oscillations can be observed. Though the glycolytic pathway is one of the most thoroughly studied metabolic systems, researchers are still debating the cause and function of these chemical oscillations. Analyzing such a large biochemical network is difficult because it is rare that all of the relevant parameters for the chemical reactions are known. For example, it is not always clear how the enzymes behave under natural conditions in the densely crowded environment of the cell. An additional difficulty that impedes both experimental and theoretical work is the dense connectivity between the elements in biochemical networks. Any attempt to study a system by artificially perturbing it will generally alter the flow of metabolites. Thus a perturbation often induces changes in all parts, which complicates inferring causal relationships, such as how accelerating one reaction influences another.
The dynamics of a metabolic pathway are typically modeled by a system of ordinary differential equations (see, for example, Refs. [2,3]). These are constructed to give the time evolution of the concentrations of the different metabolites by following the rate laws that describe the individual chemical reactions. The dynamics of the equations are then explored by numerical simulation. However, these simulations have to run for a while to actually observe the “natural” (long term) dynamics of a particular pathway. While a simulation approaches the long-term limit, it generates an instantaneous description of the system. Since this information is often not desired, it is typically discarded in the analysis. However, it costs considerable computational time and can make exploring large parameter spaces by simulation tedious. Alternatively, systems of differential equations can be studied analytically. This has the advantage of revealing the dynamics in the whole parameter space, but is limited to small pathways because of the nonlinearity and complexity of the equations.
Building on a previous study of a much simpler model [4], Gehrmann and co-workers [1] analyze glycolysis using an alternative approach called generalized modeling [5]. This approach grew out of the insight that what often prohibits analytical investigations is the computation of stationary solutions. For most real systems, computing the stationary states reveals little new information, as they are often accessible by direct observation. By contrast, analyzing the stability and dynamical transitions (bifurcations) of these stationary states, can reveal deep insights into the dynamics of the system, cutting directly to how it functions and how it could potentially fail. Once the stationary states are known, a local stability and bifurcation analysis can be carried out straightforwardly, either numerically or analytically.
The central idea of generalized modeling is to utilize the power of bifurcation analysis but avoid the difficulties of actually computing the steady states. This is accomplished by considering the whole class of models that are compatible with the structure of the pathway, instead of one specific model. Generalized modeling then uses a simple renormalization procedure to express the stability of stationary solutions as a function of specifically designed parameters. The result is a simple expression that reveals the dynamics close to every possible steady state in the whole class of models, depending on a number of parameters that can be directly interpreted in the context of the application.
In their new work, Gehrmann et al. use generalized modeling to determine under which conditions the glycolytic pathway exhibits oscillatory dynamics. Their analysis identifies one enzyme, phosphofructokinase (PFK), as an organizing center for oscillations (see inset to Fig. 1). Although previously suspected [6], the central role of PFK in oscillations has been hard to support by conclusive evidence and is still debated [7]. Here, Gehrmann and co-workers successfully untangle the complex interactions, showing clearly that PFK is central for stability. The enzyme catalyzes one of the earlier steps in the pathway, in which energy, in the form of ATP, is expended to prepare the production of more ATP at a later state. In the absence of regulation, this reaction and the subsequent ATP-producing steps would run faster if more ATP were present. Such a positive feedback of ATP on its own production would lead to a highly unstable ATP level. It is likely that to prevent this potential fatal scenario, the PFK enzyme found in nature is inhibited by ATP. Gehrmann et al.’s study shows that this negative feedback stabilizes the ATP level but may induce oscillations if the energy input into the cell is high.
Though their work suggests that glycolytic oscillations arise as a byproduct of the optimization of a stable ATP level, Gerhmann et al. point out that the oscillations may have a function, because other mechanisms utilizing the oscillatiory dynamics may have evolved later. For example, glycolytic oscillations show that the cell is well supplied with energy. Some evidence indicates that these oscillations are transmitted via signaling cascades to inform other cells of the focal cell’s energy status.
Gehrmann et al. complement their modeling with numerical simulations, which confirm and extend the predictions of the generalized model. The combination of these two approaches gives a much fuller picture of glycolosis than either approach on its own. Generalized models can efficiently explore large parameter spaces and untangle causal relationships between the systems constituents. By contrast, simulation of conventional models reveals much more detailed information on the dynamics at specific points of parameter space. For instance, the authors use simulations to investigate the effect of noise, showing that the ATP level, especially, is very robust to external perturbations. This provides further evidence for the hypothesis that the pathway is optimized for stable ATP supply.
Gehrmann et al.’s paper could well become a model example for exploring large biochemical pathways. In particular, it is conceivable that subsequent studies will use generalized models as a high-throughput prescreening tool for identifying interesting parameter sets that are then explored in more detail by simulations.
References
- E. Gehrmann, C. Gläßer, Y. Jin, B. Sendhoff, B. Drossel, and K. Hamacher, Phys. Rev. E 84, 021913 (2011)
- J. Wolf et al., Biophys. J. 78, 1145 (2000)
- F. Hynne et al., Biophys. Chem. 94, 121 (2001)
- R. Steuer et al., Proc. Natl. Acad. Sci. U.S.A. 103, 11868 (2006)
- T. Gross and U. Feudel, Phys. Rev. E 73, 016205 (2006)
- A. Goldbeter, FEBS Letters 43, 327 (1974)
- M. Bier et al., Biophys. Chem. 62, 15 (1996)