Embracing Quantum Metrology with Wide Arms

Jörg Schmiedmayer; Markus Arndt

Viewpoint

Embracing Quantum Metrology with Wide Arms

Jörg Schmiedmayer

Vienna Center for Quantum Science and Technology, Atominstitut, University of Technology, Vienna, Stadionallee 2, 1020 Vienna, Austria

Markus Arndt

Vienna Center for Quantum Science and Technology, Faculty of Physics, University of Vienna, Boltzmanngasse 5, 1090 Vienna, Austria

September 19, 2011• Physics 4, 74

New beam splitter techniques extend the world of precision experiments with matter waves.

Figure caption — **Figure 1:** (a) A Bose Einstein condensate is vertically launched in the vacuum chamber and exposed to a series of coherent manipulation processes. (b) Carefully chosen pulse sequences result in division into two separate wave packets (the “beam splitter”), swapping the momentum states of the two emerging partial wave packets (the “atom mirror”), and recombination by a second “beam splitter”, identical to the first one. (c) All three optical elements can be achieved by a combination of two judiciously tuned vertically counterpropagating laser beams (f1 and f2), which transfer the momentum of six photons per pulse onto the atoms. The $102 ħ k$ interferometer consists of $17$ such pulses in a single beam splitter sequence and up to $33$ pulses to realize the mirror. The laser intensity determines whether the light acts as a beam splitter or a mirror. The location of the atomic wave packets at the interrogation time can be visualized by detecting the shadow images on a CCD camera when the atoms are illuminated by resonant laser light from the side.

Interferometers are counted among the best tools for precision experiments. Interference metrology with light was even used to define the unit of length until $1960$ and the best gravitational wave antennae are optical interferometers searching for space deformations on the scale of below $Δ L / L \sim 10^{- 22}$ . This is possible because the light wave carries its own ruler whose scale length, the wavelength, is both very small and known with very high precision.

Quantum physics predicts a very close analogy between light and matter: It describes them both as dual objects, exhibiting the properties of both particles and waves. The concept of matter-waves stimulated the development of formal quantum mechanics and it is nowadays exploited in fine tools for fundamental and precision measurements using atom interferometry [1]. In such experiments the atomic wave amplitude is first coherently split in two or more parts. These partial waves propagate freely until their dynamics is reversed and the waves are recombined to interfere. Forces or potentials along the way will modify the resulting interference pattern. Atom interferometers are therefore natural quantum sensors and their scale length is determined by the effective (transverse) atomic de Broglie wavelength. This is inversely proportional to the momentum that is given to the atom by the beam splitter. When using laser-based optical gratings to split the beam, the strength of the kick grows with the number of the coherently scattered photons, and the precision of laser interferometers can be transferred to atom interferometers through the precision of the momentum imparted by a single photon.

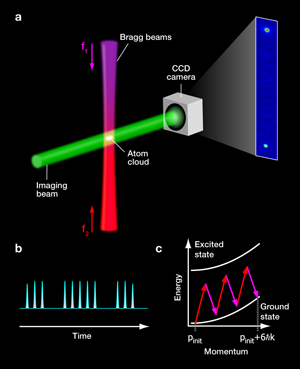
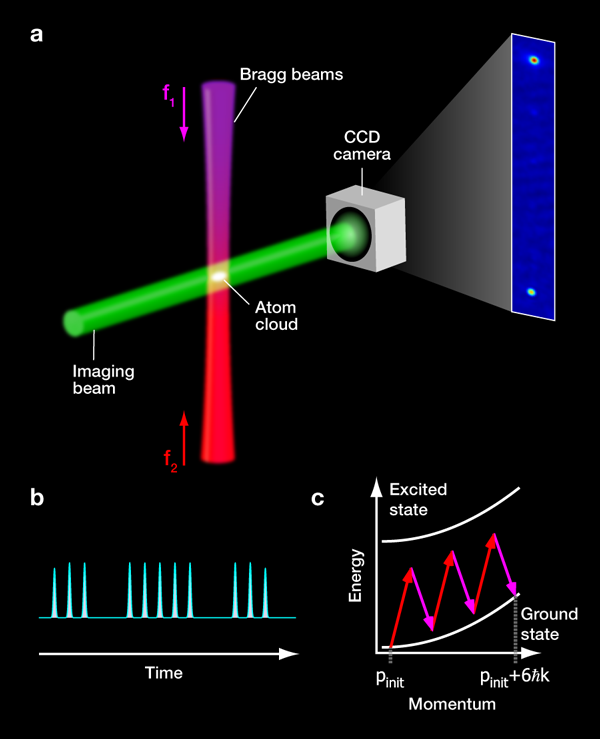
In a paper now appearing in Physical Review Letters, Sheng-Wey Chiow and colleagues from Stanford University, California, demonstrate an atom interferometer (Fig.1) that uses a sequence of refined optical laser pulses which coherently split the atomic momentum by more than $100$ times the photonic recoil [2]. This is almost five times stronger than in comparable earlier studies. It reduces the scale length of the atomic “meter stick” to $1 / 100$ of the laser wavelength and thus opens new possibilities for many quantum sensing applications.

Historically, systematic studies of atomic diffraction and coherence only became accessible with the first tailor-made optical [3] beam splitters for atoms—and many others have been developed since then [1,4–6]. One approach relies on absorptive mechanical gratings [7], which are conceptually simple and work for any atomic species, but the momentum transfer at a nanostructure of period $d$ is $p = h / d$ . It is limited by the smallest structure that can be reliably fabricated. Typical values are $d = 100 nm$ , i.e., about a fifth of the wavelength of visible light, and further reduction is often neither feasible nor physically desirable as the atom-grating interaction via van der Waals forces would introduce additional phase shifts. In contrast to that, an optical beam splitter, such as realized by diffraction at a thin standing laser light wave, is based on the coherent exchange of an integer number of photons between the atom and the laser beam. Optical gratings are highly transparent and the photon momentum is known with the same precision as the laser frequency. Bragg scattering extends this idea to the diffraction at an extended standing light wave, which has a much higher directional selectivity than the diffraction at thin beams. In principle, high momentum transfer can be achieved by high-order Bragg scattering. This is mostly limited by the available laser power.

In the new experiment by Chiow et al. the large momentum transfer is achieved by a clever combination of sequential Bragg pulses. In a first step, third-order Bragg scattering is used to split the atomic wave function in two parts, thus separating the diffracted beam from the unperturbed part by $Δ p = 6 ħ k$ . With the laser intensity properly adjusted this realizes a $50$ : $50$ beam splitter. A series of Bragg pulses then transfers sequentially more momentum to the diffracted beam up to a total $102 ħ k$ in $17$ pulses. They all need to be precisely tuned so that the atomic beam fulfils the Bragg condition, even when it changes its velocity due to the transfer and in the presence of gravity. To build a closed atom interferometer a set of $33$ further pulses—differently tuned, to exchange the momenta of the two split atomic waves—“reflects” and reconverges both arms. The interferometer is finally closed by recombining the waves at a third beam splitter, which is a time-reversed copy of the first pulse series.

A big challenge in the implementation of this concept is the timing and intensity control that is required to achieve the highest possible population transfer efficiency into the desired momentum states. In the Stanford experiments, each $6 ħ k$ pulse has an efficiency of $94 %$ , corresponding to an impressive value of $99 %$ per single photon.

Similar ideas for large-angle beam splitters were also developed by Müller et al. who combined Raman beam splitting with Bloch oscillations to achieve an effective beam separation by as much as $88 ħ k$ and a full-fledged interferometer with an internal atomic beam splitting of $24 ħ k$ with a combination of Bloch-Bragg-Bloch gratings [8,9].

One of the most promising applications of large-momentum-transfer beam splitters is in wide-area interference sensors where the atom acts as an inertial system in free fall, and the relative motion of the laboratory is measured by the acquired phase shift. The Stanford interferometer is so sensitive that inertial effects and interferometer vibrations prevented the observation of a steady fringe pattern. Instead, the interference revealed itself in the statistical distributions of the counts in the complementary output ports. Adding a second Bragg beam splitter up front allowed the team to build two parallel interferometers in such a way as to measure only force gradients, and to eliminate common inertial effects. The interferometer output ports were highly correlated, showing that high-contrast interference measurements are possible.

The Stanford beam splitter may soon become a part of a metrological device of utmost sensitivity. In an atomic fountain with a $1 s$ interrogation time, a $100 ħ k$ beam splitter will lead to meter-scale wave-packet separations. Assuming a flux of $10^{6}$ atoms/second, an interferometer could reach an acceleration sensitivity down to $10^{- 13} g / \sqrt{Hz}$ or a shot-noise-limited measurement of fundamental constants, such as $ħ / m_{Rb}$ with a sensitivity of $10^{- 12} ħ / m_{Rb} / \sqrt{Hz}$ . Aiming at compactness and transportability rather than ultimate sensitivity, the $100 ħ k$ beam splitter could be the key to a $1 cm$ short accelerometer with a sensitivity of $\sim 10^{- 9} g / \sqrt{Hz}$ , i.e., by far good enough to search for gravitational anomalies and dynamics on Earth, including the prospection for natural resources.

To further improve the sensitivity of such atom interferometers it is natural to increase the beam splitting momentum transfer even further. Any progress here contributes linearly to the final precision and even $1000 ħ k$ are not excluded by the laws of physics and foreseeable technology [2,8]. Alternatively, one may also increase the measurement time, which enhances the sensitivity to inertial effects quadratically. This strategy is currently explored in drop tower experiments [10] and discussed in feasibility studies for space experiments [11]. A shot noise limited signal can also be improved in proportion to $\sqrt{N}$ where $N$ is the number of atoms contributing to the signal. Finally, number squeezed input states [12] could even allow one to achieve sub-shot-noise sensitivity and Heisenberg limited interferometry [13] whose sensitivity scales with $N$ instead of $\sqrt{N}$ .

High-sensitivity atom interferometers will soon be implemented in the field, for instance in monitoring systems in geodesy, i.e., for measuring the Earth’s gravitational contours and evolution. They may reach their highest resolution when deployed in space, where they may serve in high-precision measurements on general relativity, such as the equivalence principle or the Lense-Thirring effect (a torsion of spacetime in the vicinity of rotating bodies), or possibly even characterize gravitational waves.

References

A. D. Cronin, J. Schmiedmayer, and D. E. Pritchard, Rev. Mod. Phys. 81, 1051 (2009)
S-w. Chiow, T. Kovachy, H-C. Chien, and M. A. Kasevich, Phys. Rev. Lett. 107, 130403 (2011)
P. E. Moskowitz et al., Phys. Rev. Lett. 51, 370 (1983)
C. Bordé, Phys. Lett. A 140, 10 (1989)
D. W. Keith et al., Phys. Rev. Lett. 66, 2693 (1991)
M. Kasevich and S. Chu, Phys. Rev. Lett. 67, 181 (1991)
D. W. Keith, et al., Phys. Rev. Lett. 61, 1580 (1988)
H. Müller et al., Phys. Rev. Lett. 102, 240403 (2009)
H. Müller et al., Phys. Rev. Lett. 100, 180405 (2008)
W. Ertmer, E. M. Rasel, and the QUANTUS Team, Nucl. Phys. B Proc. Suppl. 166, 307 (2007)
W. Ertmer et al., Exp. Astron. 23, 611 (2008)
C. Gross et al., Nature 464, 1165 (2010)
L. Pezzé and A. Smerzi, Phys. Rev. Lett. 100, 073601 (2008)

About the Authors

Jörg Schmiedmayer is Professor of Physics at the TU-Wien (Vienna University of Technology) He received his doctoral degree in nuclear physics from the TU-Wien (1987). After a postdoc in Vienna and Oak Ridge he changed to quantum physics and went as a research scientist to Harvard and MIT. In 1995 he joined A. Zeilinger in Innsbruck where he developed integrated matter-wave optics and the atom chip. Before coming back to the TU-Wien in 2007 he held a chair in experimental physics in Heidelberg. His research interests cover a wide range, from many-body quantum physics with ultracold atoms to interconnecting quantum systems from photons, atoms, and spins, and superconducting quantum circuits.

Markus Arndt is a Professor of Physics at the University of Vienna and head of the Quantum Nanophysics Group. After his Ph.D. with Antoine Weis and Theodor W. Hänsch at MPQ Garching and LMU Munich he spent two years with Jean Dalibard at the ENS Paris where he worked on ultracold atoms, atom optics, and atom interferometry. In 1997 he joined Anton Zeilinger as a postdoc in Innsbruck to jointly start the field of macromolecule interferometry. He moved to Vienna in 1999 where he has worked ever since. His current interests cover matter-wave interferometry, molecular quantum optics, quantum-enhanced molecule metrology, molecular sources, detectors, and cooling methods as well as the interface between quantum physics and biology.