Disorder Makes a Robust Matter-Wave Interferometer

Sergey E. Skipetrov

Viewpoint

Disorder Makes a Robust Matter-Wave Interferometer

Sergey E. Skipetrov

Université Grenoble 1/CNRS, Laboratoire de Physique et Modélisation des Milieux Condensés UMR 5493, B.P. 166, 38042 Grenoble, France

November 5, 2012• Physics 5, 123

Ultracold atoms can coherently scatter backwards from a disordered potential in a way similar to classical waves.

Figure caption — **Figure 1:** (a) Multiple scattering of a plane wave with a wave vector $k_{i}$ at points $1$ , $2$ , …, $n - 1$ , $n$ changes its wave vector to $k_{f}$ . The angular distribution of multiply scattered intensity $I (k_{f})$ results from the interference of waves scattered along all possible paths. It is a random function of $k_{f}$ because the phases of different waves differ by more that $2 π$ and hence can be considered random. This random intensity distribution is called a “speckle pattern.” (b) When the speckle pattern $I (k_{f})$ is averaged over many realizations of the disordered potential, its random spatial structure washes out, whereas a peak builds up in the backscattering direction $k_{f} = - k_{i}$ . This coherent backscattering (CBS) results from the constructive interference of time-reversed waves that follow the same scattering path in opposite directions.

When a coherent wave scatters from a disordered medium, it creates a random interference pattern known as “speckle.” We can easily observe speckle patterns in reflections of a laser pointer from a rough wall, for example. They are, however, completely washed out upon averaging over an ensemble of different arrangements of scattering objects. Coherent backscattering (CBS) is a unique interference effect that, on the contrary, builds up upon ensemble averaging—a peak in the direction opposite to the direction of the incident wave appears in the averaged signal, though it is not visible in a single arrangement of scatterers. This effect is a signature of wave coherence and a sensitive probe of the scattering medium because its shape depends on the statistical properties of the latter. It was shown to exist for many types of waves, from electrons in disordered solids [1] to light in colloidal suspensions [2,3] and seismic waves [4]. In a recent paper in Physical Review Letters, Fred Jendrzejewski at the University of Paris-Sud, France, and co-workers [5] report on its observation for ultracold atoms in random optical potentials. In contrast to previous experiments, CBS has now been measured using a macroscopic quantum object—the Bose-Einstein condensate—and inside the region of space where the disordered potential exists. CBS may become a powerful tool to study fine features of matter-wave propagation in the presence of disorder. Such studies are likely to substantially improve our understanding of this particular problem, as well as shine new light on those of its aspects that are general for all waves.

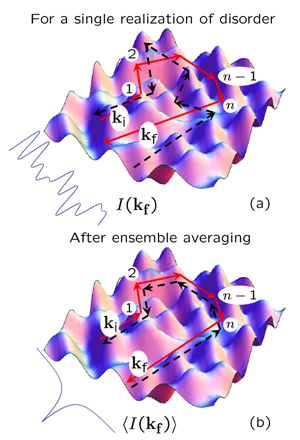
The phenomenon of CBS is very easy to understand. Imagine a monochromatic plane wave that has a frequency $ν$ and a wave vector $k_{i}$ ( $i$ for initial) and that undergoes a sequence of elastic scattering events at points $1$ , $2$ ,…, $n - 1$ , $n$ in a disordered medium (Fig. 1). Assuming the scattering is elastic, the frequency of the wave remains the same, whereas its wave vector changes to $k_{f}$ ( $f$ for final). The intensity pattern that one observes results from the interference of such waves that follow various multiple-scattering paths in the medium. What does this interference pattern look like? Under conditions of weak scattering, when the typical distance between two scattering events is much larger than the wavelength, two paths that differ by just a single scattering event will typically acquire a phase difference much larger than $2 π$ . As a consequence, the result of their interference can be considered random, and the interference pattern will be a random arrangement of bright and dark spots—the speckle pattern [Fig. 1(a)].

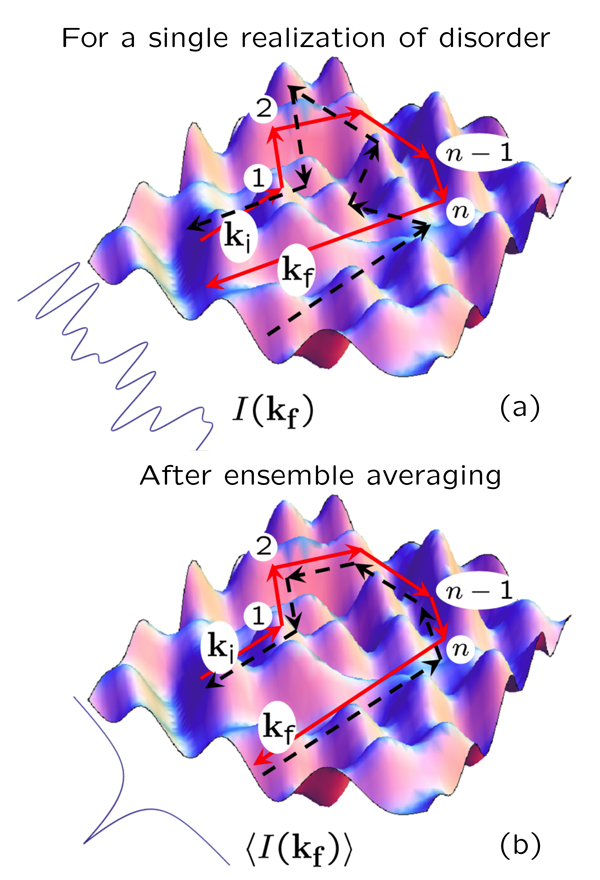
An attentive reader might notice, however, that if the second wave of a pair follows exactly the same path as the first one, but in the opposite direction, the phases of the two waves will be equal, and they will interfere constructively. For the path that we considered above, for example, the coherent partner path will be the one that starts with $k_{i} = - k_{f}$ and experiences scattering at points $n$ , $n - 1$ , etc. Finally, after the last scattering event at the point 1, the partner path acquires a wave vector $k_{f} = - k_{i}$ [Fig. 1(b)]. But for a single realization of disorder, the constructive interference of waves that follow these time-reversed paths is not visible because many other completely different pairs of paths can accidentally end up with a phase difference equal to $0$ , to $2 π$ , or to a multiple of $2 π$ , and thus lead to a constructive interference.

The difference between the interference of time-reversed paths and that of pairs of paths having nothing in common becomes clear when we average the speckle pattern over many arrangements of scattering objects. The constructive interference of two different paths that accidentally took place for a given arrangement turns into destructive interference for another one and, as a result, no interference effect remains after ensemble averaging. On the contrary, the interference of pairs of time-reversed paths is always constructive and thus survives ensemble averaging. This gives rise to a peak of intensity in the backscattering direction [Fig. 1(b)]. Indeed, the two waves of equal amplitudes $A$ that add up incoherently at $k_{f} \neq - k_{i}$ give rise to the intensity $I_{incoh} = | A |^{2} + | A |^{2} = 2 | A |^{2}$ , whereas the constructive interference at $k_{f} = - k_{i}$ yields $I_{coh} = | A + A |^{2} = 4 | A |^{2} = 2 I_{incoh}$ . The intensity of the backscattered wave is twice the intensity of waves scattered in other directions.

The experiment of Jendrzejewski et al. [5] follows the above scenario with a Bose-Einstein condensate of ultracold atoms playing the role of a coherent wave: an atom with energy $E$ and momentum $p$ can be associated with a wave of frequency $ν = E / h$ and wave vector $k = 2 π p / h$ , where $h$ is the Planck constant. The atoms scatter in a disordered optical potential (an optical speckle created by passing a coherent laser through a diffuser) and can change their direction of propagation randomly. After a long time, however, a large fraction of them “prefer” to go in a direction that is exactly opposite to their initial direction of propagation. This is a manifestation of CBS phenomenon due to the interference of multiply scattered matter waves.

It is important to realize that the Bose-Einstein condensate of cold atoms used in the experiment is a macroscopic object (size $> 30$ micrometers) and that it is not a priori obvious that the spatial coherence needed for the wave properties to be observable survives scattering by a disordered potential under conditions of a real experiment. Of course, other interference experiments were performed with Bose-Einstein condensates previously [6]. As in all standard observations of interference, they required careful experimental arrangements to guarantee the symmetry between the two interfering parties because any change of the phase difference between them would affect the result of interference. Using a disordered potential as an interferometer for matter waves seems to avoid these difficulties: the perfect symmetry between the two interfering time-reversed paths results from the time-reversal symmetry of the cold atomic system and does not depend on the scientist performing the experiment. As paradoxical as it may seem, disorder makes interference robust!

The actual experiment reported by Jendrzejewski et al. is a bit more involved than the simple situation that we described above. The Bose-Einstein condensate is not described by a single plane wave but by a wave packet with a certain spread of energies $Δ E$ and momenta $Δ p$ . The spread over energies helps to achieve averaging despite a limited ensemble of independent measurements ( $20$ in the experiment), obtained by repeating the experiment with different but statistically equivalent disordered potentials. This is because summing over different (but still sufficiently close) energies is roughly equivalent to averaging over different realizations of disorder. The spread over momenta introduces a time scale $t_{Δ p} \sim h^{2} / D | Δ p |^{2}$ that governs the time evolution of CBS. This time scale depends on the diffusion constant of atoms in the disordered potential $D$ , which is an important transport parameter and which can be measured by observing the width and the height of the CBS peak as functions of time. In addition, the comparison of the full angular distribution of scattered atoms with theoretical predictions [7] gives access to other transport parameters, such as the scattering and transport mean-free times. Thus these measurements are a powerful tool to probe coherent transport in the presence of disorder and are likely to give access to new information that may be extremely valuable even beyond the field of cold-atom physics. An independent measurement on CBS of a Bose-Einstein condensate by G. Labeyrie et al. [8] reports results that are similar to those of Jendrzejewski et al. [5] and confirms this conclusion.

The experimental techniques developed by Jendrzejewski et al. give access to CBS in the region of space where the disordered potential is present, whereas previous CBS measurements were performed outside disordered media. A straightforward application of these techniques would be the measurement of CBS under conditions of strong scattering, when Anderson localization—a halt of wave transport due to interference effects—takes place [9]. According to theoretical predictions [7], such a measurement may be very useful to better understand the physics of this regime of wave propagation and to directly measure the localization length. Moreover, a novel phenomenon—coherent forward scattering—was recently predicted to take place at strong disorder [10]. It should lead to a peak in forward direction (i.e., at $k_{f} = k_{i}$ ) in the momentum distribution of scattered atoms. The work of Jendrzejewski et al. paves the way towards experimental observation of this phenomenon.

References

G. Bergmann, “Weak localization in Thin-Films a Time-of-Flight Experiment with Conduction Electrons,” Phys. Rep. 107, 1 (1984)
M. P. van Albada and A. Lagendijk, “Observation of Weak Localization of Light in a Random Medium,” Phys. Rev. Lett. 55, 2692 (1985)
P.-E. Wolf and G. Maret, “Weak Localization and Coherent Backscattering of Photons in Disordered Media,” Phys. Rev. Lett. 55, 2696 (1985)
E. Larose, L. Margerin, B. A. van Tiggelen, and M. Campillo, “Weak Localization of Seismic Waves,” Phys. Rev. Lett. 93, 048501 (2004)
F. Jendrzejewski, K. Müller, J. Richard, A. Date, T. Plisson, P. Bouyer, A. Aspect, and V. Josse, “Coherent Backscattering of Ultracold Atoms,” Phys. Rev. Lett. 109, 195302 (2012)
M. R. Andrews, C. G. Townsend, H. J. Miesner, D. S. Durfee, D. M. Kurn, and W. Ketterle, “Observation of Interference Between Two Bose Condensates,” Science 275, 637 (1997)
N. Cherroret, T. Karpiuk, C. A. Müller, B. Grémaud, and Ch. Miniatura, “Coherent Backscattering of Ultracold Matter Waves: Momentum Space Signatures”, Phys. Rev. A 85, 011604 (2012)
G. Labeyrie, T. Karpiuk, J.-F. Schaff, B. Grémaud, C. Miniatura, and D. Delande, “Coherent Backscattering of a Dilute Bose-Einstein Condensate,” arXiv:1206.0845
F. Jendrzejewski, A. Bernard, K. Müller, P. Cheinet, V. Josse, M. Piraud, L. Pezze, L. Sanchez-Palencia, A. Aspect, and P. Bouyer, “Three-Dimensional Localization of Ultracold Atoms in an Optical Disordered Potential,” Nature Phys. 8, 398 (2012)
T. Karpiuk, N. Cherroret, K. L. Lee, B. Grémaud, C. A. Müller, and C. Miniatura, “Coherent Forward Scattering Peak Unveiled by Anderson Localization,” arXiv:1204.3451

About the Author

Sergey E. Skipetrov is a research fellow of the French National Center for Scientific Research (Centre National de la Recherche Scientifique, CNRS) working in Grenoble, France. He obtained his Ph.D. degree in physics and mathematics from M.V. Lomonosov Moscow State University in 1998 and his Habilitation in physics from the J. Fourier University in Grenoble, in 2007. His main scientific interests lie in the field of wave propagation in random media, with applications in condensed-matter physics and quantum optics.