Lasers of Pure Sound

José Tito Mendonça

Viewpoint

Lasers of Pure Sound

Instituto Superior Técnico, 1049-001 Lisbon, Portugal

March 18, 2013• Physics 6, 32

Phonon lasing—coherent amplification of phonons by stimulated emission—has been achieved in a purely acoustic analog of a three-level laser scheme.

Figure caption — **Figure 1:** (Top) Three-level scheme for a conventional optical laser. (Bottom) Three-level scheme of the phonon laser reported by Mahboob *et al.* [1]. The mechanical laser cavity features three energy levels, where only phonon transitions are allowed. The laser is pumped to the upper level $ω_{H}$ by a piezoelectric transducer, and stimulated amplified phonon decay radiation onto the intermediate level $ω_{M}$ is observed at a frequency $ω_{L} = ω_{H} - ω_{M}$ . Inset: electron micrograph of the electromechanical resonator used by Mahboob *et al.*

The theoretical foundations for the laser were established in 1917, when Einstein formulated the quantum theory of radiation, describing the absorption, spontaneous emission, and stimulated emission of electromagnetic radiation. Its realization stayed hidden for decades, however, before it emerged in the form of masers and lasers, which emit microwave and visible radiation, respectively. The range of emitted frequencies was soon broadened to cover wavelengths from the infrared to the x-ray range, and lasing was extrapolated beyond the realm of optics. Free-electron lasers, in which the active medium is a relativistic electron beam, helped cover extreme wavelength ranges and are now the basis for a new generation of experimental facilities for x-ray experiments. Atom lasers—emitting matter waves instead of photons—have also been demonstrated. Recently, the laser idea was extended to sound waves, leading to the conceptualization of the acoustic analog of a laser, which emits phonons (lattice vibrations) instead of photons. Now, writing in Physical Review Letters, Imran Mahboob at the NTT Basic Research Laboratories, Japan, and colleagues report on the experimental demonstration of a purely mechanical counterpart of a three-level laser scheme [1]. The device, excited by acoustic vibrations, amplifies sound waves through stimulated emission of phonons and acts as a phonon laser: a spectrally pure source of phonons with a frequency of around $1.7$ megahertz (MHz).

What is the appeal of phonon lasers? One potential advantage is that their emission has smaller wavelength than that of photon lasers at the same frequency because the sound speed is much smaller than the speed of light. This could help improve the resolution of tomographic, ultrasound, and other imaging techniques. In analogy with their optical cousins, phonon lasers might deliver directional and coherent acoustic beams, which could be coupled to nanoscale mechanical engines or used in communication networks based on acoustic waves. But as the history of optical lasers suggests, most applications of future phonon lasers may be completely unexpected.

In the last decade, the realization of a phonon laser has been pursued using different approaches, involving semiconductor quantum wells [2], nanomechanical devices [3], nanomagnets [4], single trapped ions [5], or a laser-cooled gas [6]. Fully coherent emission of phonons has been demonstrated only recently, by using hybrid optomechanical schemes in which the stimulated emission of phonons is driven by photons: optically pumped microcavities were shown to produce stimulated acoustic emission in the range of hundreds of megahertz [7] and in the terahertz range [8]. Using a similar approach, the generation of coherent and monochromatic phonons was achieved in a vertical cavity surface laser designed to be resonant for both photons and phonons at the same wavelength [9]. However, the need for optical pumping in such architectures may severely limit the development of phonon lasers because unavoidable compromises have to be made when designing a scheme that is simultaneously resonant for both phonons and phonons. Hence, the development of a purely mechanical phonon laser would pose a major breakthrough.

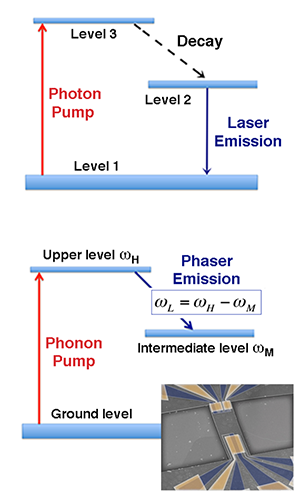
Now, the paper of Mahboob et al. reports a significant step towards this goal. The authors create a purely mechanical system of three energy levels that is reminiscent of a three-level laser scheme (see Fig. 1, top panel). In a three-level laser, atoms are excited by an optical pump (usually another laser or a flashlamp) from the ground level (1) to a higher energy level (3), and then quickly relax through spontaneous emission and accumulate in the upper laser level (2). If the population of level $2$ exceeds that of level $1$ (a condition known as population inversion), photons resonant with the $1 \to 2$ laser transition get amplified through stimulated emission: the medium acts as an optical amplifier and, when placed within a cavity, lasing occurs if the gain exceeds the losses.

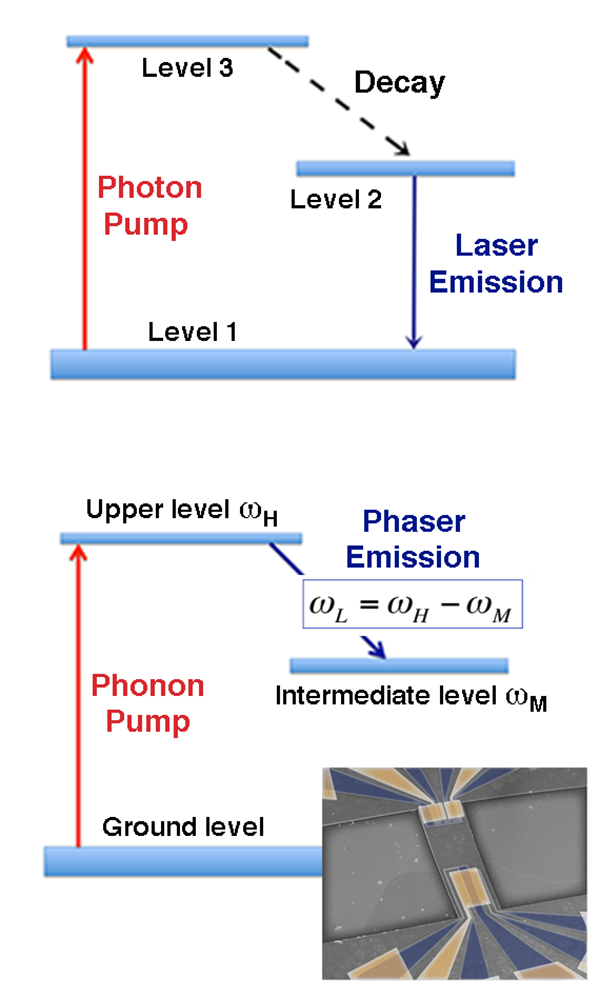
Similarly, the electromechanical resonator used by the authors can mimic the behavior of an atomic system with discrete energy levels. The resonator is a micrometer-sized GaAs-based heterostructure beam, clamped on two sides (see Fig. 1, bottom panel inset), that behaves as a high-quality-factor “phonon cavity,” with a set of well-defined vibrations whose frequencies could be manipulated piezoelectrically via external electrodes [10]. In the scheme, the three-level system is composed of three coupled acoustic modes of vibrations, as illustrated in Fig. 1 (bottom panel). The lowest-frequency acoustic mode ( $ω_{L}$ ) is a fundamental flexural mode of the resonator (flexural modes, also known as Lamb waves, are vibrations of a solid plate with motions both along the plane and in a direction perpendicular to the plane). The middle and upper modes, $ω_{M}$ and $ω_{H}$ , are other composite (flexural-torsorial-overhang) modes of the same mechanical cavity. The modes have frequencies in the MHz range and narrow bandwidths (below $40 Hz$ ). The authors excite the upper level at a frequency $ω_{H}$ via the piezoelectric actuator and, by applying a constant bias voltage to the piezoelectric electrodes, tune the frequency of the lower mode to attain the resonance condition $ω_{L} = ω_{H} - ω_{M}$ . Upon resonance, excitation of the upper level results in the amplified emission of acoustic radiation, corresponding to a stimulated transition between the upper and the intermediate energy levels.

The authors show that the device exhibits the classic hallmarks of lasing. First, the phonon emission has a clear threshold as a function of pump intensity: in lasers, the threshold corresponds to the minimum excitation level at which the output starts to be dominated by stimulated, rather than spontaneous, emission. Second, above threshold, the output level increases much more steeply with the pump power and then saturates to a linear regime. This is another characteristic feature of a laserlike instability: in a saturation regime, the gain is sufficiently high that each of the additional pump phonons injected into the cavity ( $ω_{H}$ ) decays into two lower frequency phonons, at $ω_{L}$ and $ω_{M}$ . Finally, clear evidence for lasing action is given by the spectral purity of the emitted lower-mode phonon: continuous wave lasers are spectrally coherent sources that emit light at a very precise frequency. Here, the bandwidth of the mode at low frequency is as narrow as $175$ millihertz (about a part in ten millions of the carrier frequency).

The observed behavior is due to purely acoustic radiative transitions, in which phonons are amplified through stimulated phonon emission. The three energy levels of the cavity mechanical modes play the role of the internal quantum states of the active medium of a laser, and the laser pump is replaced by the piezoelectric actuator, which excites the upper-frequency mode. Finally, intermodal coupling (the fact that the oscillation of one mode modifies the dynamics of the other modes) poses a mechanism by which energy is transferred between mechanical energy levels. This phonon lasing process is reminiscent of so-called “optical parametric” effects in a nonlinear optical crystal, in which a pump photon is divided into two photons, the sum energy of which equals the energy of the pump photon.

The experiments of Mahboob and collaborators represent an important step towards the development of a new class of entirely mechanical phonon lasers or, as some (including me) prefer to call them, inspired by Star Trek’s fictional weapon: “phasers” (short for phonon amplification by stimulated emission of radiation). A number of questions remain to be addressed: How can the coherent acoustic beam be coupled to the outside world? Will the beam feature spatial and temporal coherence properties similar to those of an optical laser beam? Further research may also take advantage of the same principles to devise amplification stages that further boost the output energy of the emitted sound waves. A modern version of the trumpets of Jericho may be approaching—hopefully, with less destructive results.

References

I. Mahboob, K. Nishiguchi, A. Fujiwara, and H. Yamaguchi, “Phonon Lasing in an Electromechanical Resonator,” Phys. Rev. Lett. 110, 127202 (2013)
H. C. Liu, C. Y. Song, Z. R. Wasilewski, A. J. SpringThorpe, J. C. Cao, C. Dharma-wardana, G. C. Aers, D. J. Lockwood, and J. A. Gupta, “Coupled Electron-Phonon Modes in Optically Pumped Resonant Intersubband Lasers,” Phys. Rev. Lett. 90, 077402 (2003)
I. Bargatin and M. L. Roukes, “Nanomechanical Analog of a Laser: Amplification of Mechanical Oscillations by Stimulated Zeeman Transitions,” Phys. Rev. Lett. 91, 138302 (2003)
E. M. Chudnovsky and D. A. Garanin, “Phonon Superradiance and Phonon Laser Effect in Nanomagnets,” Phys. Rev. Lett. 93, 257205 (2004)
A. E. Kaplan, “Single-particle Modulational Oscillator Powered by Laser,” Opt. Express 17, 10035 (2009); K. Vahala, M. Herrmann, S. Knunz, V. Batteiger, G. Saatho, T. W. Hänsch, and Th. Udem, “A Phonon Laser,” Nature Phys. 5, 682 (2009)
J. T. Mendonca, H. Tercas, G. Brodin, and M. Marklund, “A Phonon Laser in Ultra-cold Matter,” Europhys. Lett. 91, 33001 (2010)
I. S. Grudinin, H. Lee, O. Painter, and K. J. Vahala, “Phonon Laser Action in a Tunable Two-level System,” Phys. Rev. Lett 104, 083901 (2010)
R. P. Beardsley, A. V. Akimov, M. Henini, and A. J. Kent, “Coherent Terahertz Sound Amplification and Spectral Line Narrowing in a Stark Ladder Superlattice,” Phys. Rev. Lett. 104, 085501 (2010)
A. Fainstein, N. D. Lanzillotti-Kimua, B. Jusserand, and B. Perrin, “Strong Optical-Mechanical Coupling in a Vertical GaAs/AlAs Microcavity for Subterahertz Phonons and Near-Infrared Light,” Phys. Rev. Lett. 110, 037403 (2013)
I. Mahboob and H. Yamaguchi, “Bit Storage and Bit Flip Operations in an Electromechanical Oscillator,” Nature Nanotech. 3, 275 (2008)

About the Author

José Tito Mendonça is a research professor at IST Lisbon, and a former head of the Physics Department of the same institute. He is also a visiting professor at the Institute of Physics, University of São Paulo, Brazil. He has a Ph.D. from the University of Paris, Orsay. At IST Lisbon he created two research teams, one on nuclear fusion and the other on intense laser matter interaction. In recent years he has been working on quantum plasmas and laser-cooled atoms.