The Breaking of Brittle Materials
A long metal thread breaks more easily than a short one—an observation Leonardo da Vinci made in the th century. It all comes down to simple statistics: the larger an object, the more likely it is to contain a region that breaks when subject to stress. The fracture properties of brittle materials also depend on the disorder in their underlying structure: a homogeneous material like glass breaks differently than composite materials like bone and seashell. Although system size and disorder are linked in a statistical physics description of fracture, the two parameters have typically been treated separately. Now, in Physical Review Letters, Ashivni Shekhawat at Cornell University and colleagues present the first theoretical model that accounts for both at once [1]. Their model allows the authors to identify three different “phases” that characterize crack formation, and show how one phase evolves into the other as the system size or amount of disorder increases.
Even though breaking things is a daily experience, a theoretical framework to describe fracture has only emerged in the last years, starting with the seminal work by A. Griffith [2]. The bulk of existing theory is based on linear fracture mechanics, which assumes materials are perfectly homogeneous and elastic (meaning the stretching of a material varies proportionally to the load force on it, and no plastic deformation remains after the load is removed.) But such materials are rarely used in applications. Industrially important materials, like glass, can be brittle: they break under moderate stress, instead of stretching plastically like metals do. Concrete, which is made of several stones and grains of sand of various sizes, each able to sustain different loads, is both brittle and inhomogeneous (disordered).
Introducing disorder into a solid—even a purely elastic material—has an important effect on its properties, including its rigidity, lifetime, and the amount of stress it can withstand before fracturing. Linear elastic fracture mechanics can be adapted to describe these effects in materials, but doesn’t give deep insight into how fracture occurs. During the past years, however, physicists have developed new theoretical tools to deal with disordered media. Meanwhile, important experimental, numerical, and theoretical efforts to understand fracture mechanics have come from physics, engineering, and materials science.
Experiments have focused mostly on the description of crack paths, which become more jagged with disorder [3], and on the intermittency of crack propagation [4]. These experimental results have led to two main theoretical pictures. One describes the case when disorder is weak—that is, when it can be treated as a perturbation of the ideally ordered case. In this case, it has been shown that fracture of a disordered three-dimensional solid can be viewed as a dynamic phase transition: the crack front “depins” itself from the disorder [3]. In the case of strong disorder, it has been argued that fracture is a percolation phenomenon [5]. Until recently [6], however, no real unifying framework was available.
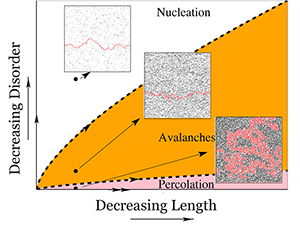
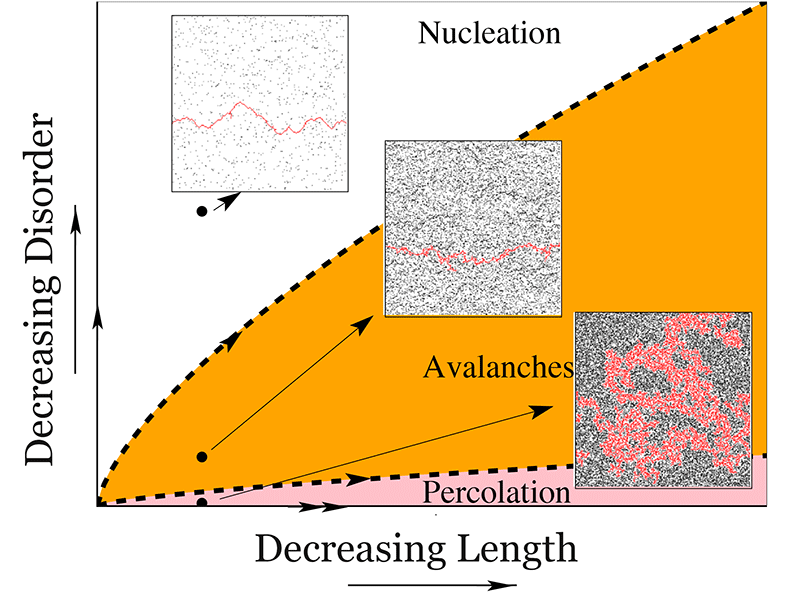
The central point of Shekhawat et al.’s paper is to propose such a unifying framework. The authors do so using a model called the random fuse network [7], which treats a break in a two-dimensional material as though it were a severed wire in a conducting mesh. The model accounts for disorder—variation in the strength of different components in the material—by giving each fuse a different current threshold for bursting. The benefit of this model is that it allows disorder to be varied continuously. The authors use the model to numerically calculate the size distributions of clusters of cracks and of avalanches (where some broken bonds trigger the fracture of neighboring bonds), and put together a scaling theory that provides a coherent picture of their results. All of this is neatly summarized in a phase diagram showing the observed types of fracture for given size and disorder (Figure 1). Specifically, the authors are able to define three regions: (i) nucleation (large systems, or little disorder), in which failure starts from a single crack that nucleates without much fracturing around it; (ii) avalanches (intermediate disorder); and (iii) percolation (very large disorder), where small cracks open in various parts of the sample and coalesce into clusters. In this latter case, failure only occurs when one of these clusters reaches the specimen size.
One of the authors’ main findings is that as a system grows, fracture is less likely to be caused by the percolation of many small cracks, whatever the amount of disorder. Rather, as the size of their fuse network grows, the probability that a critical crack will appear approaches . However, the crossover length at which this happens can be large, and clearly depends on the amount of disorder. According to this model, both percolation-like behavior and scale-invariant precursors are finite-size effects; on large length scales, a single crack always prevails.
A useful extension of this work will be to see if the results apply to other modes of fracture (the tearing mode of fracture the authors consider is usually unstable). Also, since the authors’ model is two dimensional, it would be interesting to see if the same phase diagram (Figure 1) survives in three dimensions, where the stiffness of the propagating crack front qualitatively changes the physics.
The model predicts whether failure results from the buildup of damage, or occurs in an abrupt fashion. Hence it could prove helpful in choosing the material and the size of an object in order to prevent violent failure. From the standpoint of fundamental physics, the findings are also of interest: The authors make the surprising finding that fracture is a critical phenomenon that is a mixture of discontinuous (first-order) and continuous characters. Most phase transitions are either one or the other.
References
- A. Shekhawat, S. Zapperi, and J. P. Sethna, “From Damage Percolation to Crack Nucleation Through Finite Size Criticality,” Phys. Rev. Lett. 110, 185505 (2013)
- A. Griffith, “The Phenomena of Rupture and Flow,” Philos. Trans. R. Soc. London Ser. A 221, 163 (1921)
- D. Bonamy and E. Bouchaud, “Failure of Heterogeneous Materials: A Dynamic Phase Transition?,” Phys. Rep. 498,1 (2011)
- K. J. Maloy, S. Santucci, J. Schmittbuhl, and R. Toussaint, “Local Waiting Time Fluctuations along a Randomly Pinned Crack Front,” Phys. Rev. Lett. 96, 045501 (2006)
- A. Hansen and J. Schmittbuhl, “Origin of the Universal Exponent of Brittle Fracture Surfaces: Stress-Weighted Percolation in the Damage Zone,” Phys. Rev. Lett 90, 045504 (2003)
- K. S. Gjerden, A. Stormo, and A. Hansen, “Universality Classes in Constrained Crack Growth,” arXiv:1301.2174
- M. J. Alava, P. K. Nukala, and S. Zapperi, “Statistical Models of Fracture,” Adv. Phys. 55, 349 (2006)