Pauli Principle, Reloaded

Jens Eisert

Viewpoint

Pauli Principle, Reloaded

QMIO Group, Dahlem Center for Complex Quantum Systems, Freie Universität Berlin, Arnimallee 14, 14195 Berlin, Germany

January 22, 2013• Physics 6, 8

A generalized form of the Pauli exclusion principle gives insight into the quantum wave function describing multiple electrons.

Figure caption — **Figure 1:** (Left) The electronic configuration of an atom (oxygen is shown here) is based on Pauli’s exclusion principle. (Right) A schematic showing that the generalized Pauli constraints restrict the natural occupation numbers $n_{i}$ , $n_{j}$ to the dark-blue polygon, significantly strengthening Pauli’s exclusion principle (light-blue square).

Pauli’s exclusion principle says two identical fermions cannot be in the same quantum state. In recent years, physicists have discovered a more general form of the principle that puts additional mathematical constraints on the quantum wave function describing multiple fermions. In Physical Review Letters, Christian Schilling [1] at the ETH in Zurich, Switzerland, and colleagues study a simple model to gain insight into how these additional constraints may affect the physical properties of the many-bodied wave function. Their findings may lead to new ways to simplify quantum calculations, such as those used to describe the electrons of an atom or molecule.

Wolfgang Pauli formulated his now famous principle before the advent of what is considered modern-day quantum mechanics. At the end of the second decade of the $20$ th century, physicists were starting to realize that the (at the time) mysterious periodic table could be better understood if the electrons of an atom were clustered in some way. Niels Bohr explained much of the structure and properties of atoms by assuming electrons were grouped into shells containing no more than a certain number of electrons. But in the mid 1920s it still seemed far from obvious what mechanism determined how many electrons a given atomic shell could hold. Based on work by Edmund Stoner [2], Pauli was able to explain the phenomenology of atomic spectral lines by invoking a nonmechanical “Zweideutigkeit”—or two-valuedness—of electrons [3]. He proposed that the latter would be represented by an additional quantum number taking one of two values. What is more, he suggested that no two bound electrons could have the same set of quantum numbers. The Pauli exclusion principle was born [4].

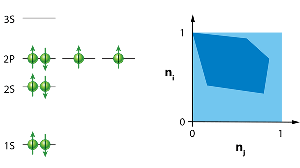
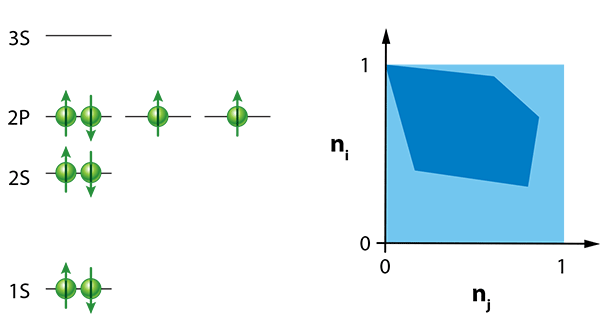
The importance of the Pauli principle can hardly be overestimated. By high school, most students are familiar with this fundamental idea, and for good reason: It explains the properties of atoms (Fig. 1) and their classification in the periodic table, gives insights into features of complex molecules and is, at the end of the day, responsible for the stability of matter [5].

Not long after the formulation of Pauli’s principle, physicists realized there was a simple yet fundamental explanation for it: the antisymmetry of the fermionic wave function. In modern terms, the principle can be formulated as stating that the natural occupation numbers of quantum states in a many-fermion system can be no larger than $1$ and no smaller than $0$ . In fact, for many practical purposes, these numbers are either very close to $0$ or very close to $1$ . This latter fact has practical consequences: To calculate the wave function in a many-fermion system, one usually starts with a good initial “guess.” Assuming a state is either occupied or empty significantly narrows down the parameter space from which this guess is made.

Given that the principle is both fundamental and, at the same time, possesses such a strong predictive power, researchers have looked for ways to generalize it, namely, by finding additional constraints on the natural occupation numbers caused by the antisymmetry of the wave function. In a groundbreaking work, Alexander Klyachko completed this task [6]: building upon earlier work (see, for example, Ref. [8]), he was able to identify new conditions on the occupation numbers, which he called generalized Pauli constraints. To understand the idea of a generalized constraint, it helps to give a concrete example. In any system of three fermions that occupy six possible states, the decreasingly ordered natural occupation numbers $λ_{i}$ of any system are constrained according to:

$λ_{1} + λ_{6} = λ_{2} + λ_{5} = λ_{3} + λ_{4} = 1$ ,

$λ_{5} + λ_{6} - λ_{4} \geq 0$ .

There is also a geometric way to represent the occupation numbers defined by the generalized Pauli constraints: the numbers must lie in a hyperdimensional, multifaceted shape called a polytope. In two dimensions, a polytope is just a polygon, such as the one shown in Fig. 1.

This is the scenario in which Schilling et al.’s work [1] comes into play. Their paper asks first if these additional constraints are “physically relevant,” meaning are they close to being saturated in a realistic problem? And second, does this abstract geometry have any practical implication for the structure of wave functions? Their analysis suggests that the answer to both questions is yes.

The authors study a simple physical model: a number of fermionic particles that interact and move around in a harmonic potential—essentially, fermionic balls in a bowl. Within their model, they can also turn a “knob,” which is the strength of the fermion-fermion interaction. If the fermions don’t interact with each other, then, in the ground state, each energy level is filled from the lowest one up to the highest one (the occupation numbers of these states are equal to $1$ ), and the antisymmetry of the wave function is ensured by making it equal to the so-called Slater determinant. But if they turn the knob and alter the interaction strength, then the natural occupation numbers associated with the lowest energy state begin to move within the region allowed by Klyachko’s constraints. The path the occupation numbers trace out as the interaction strength changes hugs very close to the boundary of the allowed region defined by the facets of the polytope. This “pinning” effect strongly suggests that the generalized Pauli constraints affect the system.

Why should this happen? When the system approaches the ground state, nature will minimize the energy until some constraint prevents it from reducing it further. Klyachko supposes that the generalized Pauli constraints might be the constraints responsible for restricting the ground-state energy [7]. This is an intriguing concept because the Pauli principle is purely kinematic (i.e., related to the set of allowed states), whereas the ground-state energy is a dynamic concept (i.e., dependent on a given Hamiltonian). Klyachko has cited numerical data in support of this intuition that kinematics might sometimes trump dynamics [7].

A central insight of the present work [1] is that this explanation is not applicable to all systems where the generalized Pauli constraints play a role. Using analytic calculations, the authors found that the natural occupation numbers in their model do not lie exactly on a facet of the allowed polytope. While the difference between “exact pinning” and the observed “quasipinning” does not show up unless calculations are extremely precise, it does imply that in the given model, one cannot think of the Pauli constraints as a wall where nature gets stuck while minimizing energy.

However, Schilling et al. go on to show that, for given natural occupation numbers, the approximate saturation of these constraints (that is, their proximity to a facet on the polytope) is enough to restrict the structure of the wave function. This is an insight that could prove most useful when devising new algorithms for simulation problems in quantum chemistry. It gives hints on how to prepare the wave function in a many-bodied system and indicates that the structure of physically relevant states of fermionic systems may be simpler than previously thought. In a way, the situation could be similar to the one found in lattice models studied in condensed-matter theory. There, the concept of entanglement entropies [9] suggests that it is possible to efficiently simulate a quantum state by using simple variational states [10,11]. The present paper does not address these possibilities in depth, but rather invites further study of the rich phenomenology of generalized Pauli constraints. Future work might uncover a physical (rather than mathematical) explanation for quasipinning and the class of models in which it occurs. Long term, researchers may find ways to use the observed structural constraints on wave functions to improve numerical algorithms.

References

C. Schilling, D. Gross, and M. Christandl, “Pinning of Fermionic Occupation Numbers,” Phys. Rev. Lett. 110, 040404 (2013)
E. C. Stoner, “The distribution of electrons among atomic energy levels,” The London, Edinburgh and Dublin Philosophical Magazine 47, 1168 (1924)
W. Pauli, “Ueber den Einfluss der Geschwindigkeitsabhaengigkeit der Elektronenmasse auf den Zeeman-Effekt,” Z. Physik 31, 373 (1925)
W. Pauli, “Ueber den Zusammenhang des Abschlusses der Elektronengruppen im Atom mit der Komplexstruktur der Spektren,” Z. Physik 31, 765 (1925)
E. J. Lieb and R. Seiringer, The stability of matter in quantum mechanics (Cambridge University Press, Cambridge, 2010)[Amazon][WorldCat]
A. Klyachko, “Quantum Marginal Problem and N-Representability,” J. Phys. 36, 72 (2006)
A. Klyachko, “The Pauli Exclusion Principle and Beyond,” arXiv:0904.2009 (2009)
R. E. Borland and K. Dennis, “The Conditions on the One-Matrix for Three-Body Fermion Wavefunctions with One-Rank Equal to Six”, J. Phys. B 5, 7 (1972)
J. Eisert, M. Cramer, and M. B. Plenio, “Area Laws for the Entanglement Entropy,” Rev. Mod. Phys. 82, 277 (2010)
F. Verstraete, J. I. Cirac, and V. Murg, “Matrix Product States, Projected Entangled Pair States, and Variational Renormalization Group Methods for Quantum Spin Systems,” Adv. Phys. 57, 143 (2008)
U. Schollwoeck, “The Density-Matrix Renormalization Group in the Age of Matrix Product States,” Ann. Phys. 326, 96 (2011)

About the Author

Jens Eisert is a full professor at the Freie Universität Berlin. Previously, he was a full professor at Potsdam University and a lecturer at Imperial College London. He received his Ph.D. in 2001. His research interests are in quantum many-body theory, quantum information theory, and quantum optics, being concerned with several implications of the study of complex quantum systems. He has been awarded several awards and prizes for his work, including a EURYI award and an ERC award.