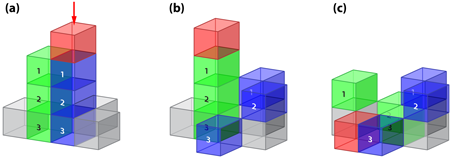
Getting Out of Control

Nuno A. M. Araújo

Viewpoint

Getting Out of Control

Computational Physics for Engineering Materials, ETH Zurich, Wolfgang-Pauli-Strasse 27, CH-8093 Zurich, Switzerland

August 12, 2013• Physics 6, 90

Complex systems—like sandpiles prone to avalanches—may become uncontrollable if too much effort is put into controlling them.

Figure caption — **Figure 1:** Schematic representation of the sandpile model used by Noël *et al.* When one grain falls on top of a pile with three grains (a), the pile becomes unstable and topples. While toppling, all grains in the pile are evenly distributed among the four neighbors (b). The toppling cascades further as one neighboring pile becomes unstable (four grains) and also topples (c).

While driving along a desert highway, we can easily predict the consequences of turning the wheel and changing lanes. However, in heavy traffic this is not the case. Traffic dynamics is complex and the response to any individual change depends on how the other drivers accommodate it [1]. This type of cooperative dynamics in complex systems makes controlling them a scientific and technological challenge [2]. Now, writing in Physical Review Letters, Pierre-André Noël and colleagues from the University of California, Davis, show that the control of complexity requires special care, as unexpected outputs can result from external intervention [3]. In particular, they show that attempts to avoid catastrophe can, in fact, push the system towards it.

In many real-world situations, one would want to devise simple schemes that can drive a system towards a desired state by applying a small perturbation [4]. For example, Youn and co-workers have shown that closing a few key roads in Boston, London, and New York can paradoxically improve the overall traffic in those cities [5]. A framework to describe many complex dynamical systems is offered by the theory of self-organized criticality (SOC). Since it was first introduced by Bak, Tang, and Weisenfeld [6], this framework has been applied to study diverse systems such as earthquakes [7], neural dynamics [8], electric grids [9], water reservoirs [10], and snow avalanches [11].

As a prototype for SOC, Bak et al. studied a model of a sandpile to which grains are constantly being added (Fig. 1). The model consists of a lattice in which each site represents a pile of grains, and at some threshold number of grains, this pile becomes unstable and topples. Iteratively, one pile is randomly chosen and one grain added to its top. When the pile topples, its total load is evenly distributed among neighbors, increasing their load. This load shedding might trigger an avalanche as neighboring piles also topple, eventually cascading further, until all piles are below the threshold.

Bak et al. calculated the avalanche size defined as the number of toppling piles in each cascade. They found that sandpiles self-organize into critical states, with many tiny avalanches and a handful of large avalanches spanning the entire system, thereby yielding a power-law avalanche-size distribution. These systems are called critical because they are reminiscent of the critical points in a second-order phase transition (e.g., a ferromagnetic transition), also characterized by power-law distributions of certain parameters. But there is an important difference. In a phase transition, a control parameter (e.g., temperature) typically drives the system from one phase to another across the critical point. By contrast, in SOC there is no control parameter and the dynamics naturally evolves towards criticality, which is why this sort of criticality is called “self-organized.” This well-studied sandpile model can only be critical in the limit of vanishing dissipation. However, dissipation is expected for certain real situations, as in water reservoirs because of evaporation, for example. In the sandpile model with dissipation, at each toppling, a fraction of grains participating in the avalanche is removed, which usually prevents the larger avalanches. The stronger the dissipation is, the larger the departure from criticality.

Noël and co-workers followed the dissipative model to address the question of how a complex network can be controlled. They imagined a system in which one could control the probability $μ$ that the next pile to be selected is one grain away from toppling. Cascades are avoided when $μ$ is lower than the natural value of the probability, i.e., the one where the sandpile is left alone; when $μ$ is raised, cascades occur more frequently. Surprisingly, the authors found that avoiding toppling (i.e., choosing too-small values of $μ$ ) can cause very large avalanches to occur more often, driving the system towards criticality. The lower the value of $μ$ , the closer the system gets to the critical state. For example, in the limit of vanishing $μ$ , criticality is observed even when half of the grains involved in the avalanche are dissipated. By contrast, when toppling is favored, small avalanches occur and the larger ones are suppressed.

In real situations, triggering cascades (large $μ$ ) would correspond to, for example, starting small forest fires to control burning or dropping snow on unstable spots in avalanche danger zones—allowing smaller avalanches prevents large-scale avalanches from emerging. Accordingly, avoiding cascades entirely (small $μ$ ) would correspond to extinguishing all forest fires or stopping snow avalanches using physical barriers. As the work of Noël et al. shows, being too zealous in controlling every small fire or avalanche may actually set the stage for larger catastrophes to occur.

The model also allowed the authors to address cost-related questions. Controlling a system imposes a cost for both the detailed interventions and for coping with the aftermath of avalanches. Is it economically preferable to have several small controlled cascades (large $μ$ ) or to handle a few large ones (small $μ$ )? The authors defined cost functions of dealing with cascades that grow nonlinearly with the avalanche size (large catastrophes are much more expensive than small ones) and analyzed the dependence of the total cost on $μ$ . They found an optimal intermediate value of $μ$ that minimizes long-term costs of cascades, which will depend on the specificities of the system.

With this simple approach, Noël et al. draw attention to nontrivial outputs resulting from human management. They show that, ideally, to avoid large scale uncontrolled events, it is important to balance the natural evolution of the system and the costs of human intervention. Direct applications of their findings will imply more realistic models tailored for each particular case.

References

D. Helbing, “Traffic and Related Self-Driven Many-Particle Systems,” Rev. Mod. Phys. 73, 1067 (2001)
Y.-Y. Lu, J.-J. Slotino, and A. L. Barabási, “Controllability of Complex Networks,” Nature 473, 167 (2011)
P-A. Noël, C. D. Brummitt, and R. M. D’Souza, “Controlling Self-Organizing Dynamics on Networks Using Models that Self-Organize,” Phys. Rev. Lett. 111, 078701 (2013)
V. H. Louzada, N. A. M. Araújo, J. S. Andrade Jr., and H. J. Herrmann, “How to Suppress Undesired Synchronization,” Sci. Rep. 2, 658 (2012)
H. Youn, M. T. Gastner, and H. Jeong, “Price of Anarchy in Transportation Networks: Efficiency and Optimality Control,” Phys. Rev. Lett. 101, 128701 (2008)
P. Bak , C. Tang , and K. Weisenfeld , “Self-Organized Criticality: An Explanation of the 1/ $f$ noise,” Phys. Rev. Lett. 59, 381 (1987)
A. Sornette and D. Sornette, “Self-Organized Criticality and Earthquakes,” Europhys. Lett. 9, 197 (1989)
L. de Arcangelis, C. Perrone Capano, and H. J. Herrmann, “Self-Organized Criticality Model for Brain Plasticity,” Phys. Rev. Lett. 96, 028107 (2006)
C. D. Brummitt, R. D’Souza, and E. A. Leicht, “Suppressing Cascades of Load in Interdependent Networks,” Proc. Natl. Acad. Sci. U.S.A. 109, E680 (2012)
G. L. Mamede, N. A. M. Araújo, C. M. Schneider, J. C. de Araújo, and H. J. Herrmann, “Overspill Avalanching in a Dense Reservoir Network,” Proc. Natl. Acad. Sci. U.S.A. 109, 7191 (2012)
J. Faillettaz, F. Louchet, and J. R. Grasso, “Two-Threshold Model for Scaling Laws of Noninteracting Snow Avalanches,” Phys. Rev. Lett. 93, 208001 (2004)

About the Author

Nuno Araújo is a senior researcher at ETH Zurich, Switzerland. He obtained his Ph.D. in physics in 2009 from the University of Minho, Portugal. His research covers different areas of the statistical physics of complex systems.