Thermal Cloaks Get Hot
Over the past few years, metamaterial scientists have used different setups and materials to show how properly engineered composites can provide a new degree of control of wave phenomena. The first metamaterials were engineered to bend microwaves in anomalous ways, followed by control of infrared radiation and light, as well as sound and mechanical waves. Now, writing in Physical Review Letters, two groups—Tiancheng Han from the National University of Singapore and colleagues, and Hongyi Xu and colleagues from Nanyang Technical University, Singapore—report independent experimental demonstrations of three-dimensional metamaterial “cloaks” for thermal flux—artificial covers capable of eliminating the disturbance created by an obstacle on the flow of heat [1,2], potentially being able to improve, for instance, thermal imaging setups.
Arguably the most exciting application of metamaterials to date is the possibility of cloaking objects, or suppressing their detectability to incoming waves of different form [3,4]. This concept has been experimentally verified at specific frequencies of operation, but we are still far from achieving broadband invisibility in the optical range for large-scale objects [5]. Beyond the challenges posed by optical waves, cloaking has been studied and proposed for sound, mechanical, seismic, and even matter waves [6,7]. This has been possible because all these phenomena are governed by wave equations, in many ways analogous to the way electromagnetic signals and light propagate. In this context, one of the most popular cloaking approaches is based on coordinate transformation [2]: a gradual inhomogeneity in a suitably tailored metamaterial cover can be mapped into a curvilinear distortion of space in an equivalent homogeneous material. This implies that light rays, which follow straight lines in homogeneous media, can be bent at will around an object by transformation-based metamaterial cloaks, eliminating wave scattering and distortion [3].
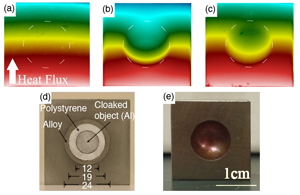
Based on the invariance of the equation governing heat conduction under analogous coordinate transformations, Guenneau et al. [8] were able to extend this technique to propose a cloak able to manipulate the heat flux. What, effectively, is the job of such a thermal cloak? Heat is governed by diffusion and therefore does not propagate in wavelike form, it actually spreads smoothly away from the source. A difference in temperature between two regions of space induces a smooth temperature gradient from hot to cold as shown in Fig. 1(a). In the long run, this thermal diffusion tends to uniformly spread the temperature field.
If we now introduce a discontinuity, or an obstacle, within the flux path, as in Fig. 1(b), the isothermal lines become distorted. For instance, a good thermal conductor appears to repel the lines towards its surface, while an insulator attracts them. A thermal cloak hides objects from diffusive heat by smoothly guiding the thermal flux around them, so that mapping the isothermal lines outside the cloaked region would not reveal the presence of the discontinuity. This is achieved in Fig. 1(c), which shows the restoration of straight isothermal lines all around the cloaked object. Xu et al. [2] here mapped the temperature field all around the object of interest at a specific instant in time, proving full restoration of the original temperature distribution, as if the object were not there.
As with electromagnetic cloaking, efficiently creating the required inhomogeneity and anisotropy profiles of Guenneau’s cloak appeared to be a severe challenge. Wegener’s group [9] showed a way to do this in a two-dimensional, planar geometry by relaxing some of the original theoretical constraints (see 10 May 2013 Focus), but the cloak was bulky and the setup appeared to be constrained to the specific planar configuration.
The two new papers [1,2] have further simplified the original constraints, inspired by an approach to cloaking previously introduced for electromagnetic and magnetostatic fields [4,10]. Rather than providing stringent inhomogeneity profiles for the cloak’s thermal conductivity, the scientists derived simple static conditions on isotropic and homogeneous cloaks that would allow maximally suppressing the heat distortion around its volume. This solution allowed elegant experimental verifications for thermal cloaking of three-dimensional objects, using thin cloaks made of common materials, such as polystyrene, metal alloys, or copper [see Fig. 1(d),(e)]. The researchers from both groups were able to prove the cloak functionality in the transient regime, while the heat diffuses before reaching equilibrium, and in steady state in an inhomogeneous temperature field.
It is important to stress that thermal cloaks cannot violate the classical laws of thermodynamics, which are still strictly preserved. Therefore, the cloak cannot prevent heat from flowing to its interior and reaching a uniform temperature field at equilibrium. Thermal cloaks appear to be of interest when thermal conductors or insulators are used to modify the transient heat flux, introducing preferred paths of thermal diffusion. In these instances, the cloak is able to maintain conduction or isolation while avoiding the disturbance on the isothermal lines around the object.
What’s next then? Beyond representing another interesting proof-of-principle for popular cloaking concepts and showing that cloaks may be able to tailor not only wave propagation but also diffusion, which may potentially impact electricity, tomography, or chemical diffusion, we can expect these cloaks to be used to improve thermal imaging or manipulate thermal flow with precision in challenging environments, e.g., on a computer motherboard. While potentially useful, I am not sure these applications are going to be as hot a topic as Harry Potter’s invisibility cloak.
References
- Tiancheng Han, Xue Bai, Dongliang Gao, John T. L. Thong, Baowen Li, and Cheng-Wei Qiu, “Experimental Demonstration of a Bilayer Thermal Cloak,” Phys. Rev. Lett. 112, 054302 (2014)
- Hongyi Xu, Xihang Shi, Fei Gao, Handong Sun, and Baile Zhang, “Ultrathin Three-Dimensional Thermal Cloak,” Phys. Rev. Lett. 112, 054301 (2014)
- J. B. Pendry, D. Schurig, and D. R. Smith, “Controlling Electromagnetic Fields,” Science 312, 1780 (2006)
- A. Alù, and N. Engheta, “Achieving Transparency with Plasmonic and Metamaterial Coatings,” Phys. Rev. E 72, 016623 (2005); A. Alù, “Mantle Cloak: Invisibility Induced by a Surface,” Phys. Rev. B 80, 245115 (2009)
- F. Monticone and A. Alù, “Do Cloaked Objects Really Scatter Less?” Phys. Rev. X 3, 041005 (2013)
- M. Kadic, T. Bückmann, R. Schittny, and M. Wegener, “Metamaterials Beyond Electromagnetism,” Rep. Prog. Phys. 76, 126501 (2013)
- R. Fleury and A. Alù, “Quantum Cloaking Based on Scattering Cancellation,” Phys. Rev. B 87, 045423 (2013)
- S. Guenneau, C. Amra, and D. Veynante, “Transformation Thermodynamics: Cloaking and Concentrating Heat Flux,” Opt. Express 20, 8207 (2012)
- R. Schittny, M. Kadic, S. Guenneau, and M. Wegener, “Experiments on Transformation Thermodynamics: Molding the Flow of Heat,” Phys. Rev. Lett. 110, 195901 (2013)
- F. Gömöry, M. Solovyov, J. Souc, C. Nacau, J. Prat-Camps, and A. Sanchez, “Experimental Realization of a Magnetic Cloak,” Science 335, 1466 (2012)