Statistical flickers in a Bose-Einstein Condensate of Photons

Cristiano Ciuti

Viewpoint

Statistical flickers in a Bose-Einstein Condensate of Photons

Cristiano Ciuti

Laboratoire Matériaux et Phénomènes Quantiques, Université Paris Diderot et CNRS, Paris, France

January 21, 2014• Physics 7, 7

Experiments with photons show that the number of particles in a Bose-Einstein condensate can have strong fluctuations.

Figure caption — **Figure 1:** A Bose-Einstein condensate of photons. (Top) Schmitt *et al.* produce a photon BEC by using an optical pump to excite dye molecules in an optical cavity. The surrounding molecules act as a heat bath and a particle reservoir. (Center) When the effective size of the reservoir is large enough, the setup produces grand-canonical conditions and Schmitt *et al.* observe large fluctuations in the number of particles in the condensate. (Bottom) These fluctuations disappear with a small reservoir.

The most familiar type of Bose-Einstein condensate (BEC) is one made of identical atoms, which, when cooled to extremely low temperatures, collectively fall into the same single-particle quantum state and form a giant matter wave. But BECs can form from other types of bosons, including polaritons and photons, and unlike atoms in an isolated trap, these particles can be easily created or destroyed within the medium in which they are produced. Researchers have now revealed unusual statistical effects in a BEC that can exchange particles and energy with such a medium. Julian Schmitt and colleagues at the University of Bonn, Germany, produced a BEC of photons within a bath of photoexcitable dye molecules that acted as a “reservoir” of photons and a heat bath, showing that particle fluctuations in the condensate could be a substantial fraction of the total number of particles [1]. Their experiment, reported in Physical Review Letters, is a rare example of a quantum gas in the so-called grand-canonical ensemble of statistical physics. Their work also shows that it is possible to make a BEC in which particle number isn’t conserved, thereby addressing a long-standing question in statistical physics.

Like other systems containing large numbers of particles, BECs are described statistically. Different statistical ensembles, that is, large numbers of particles prepared under specific thermodynamic conditions, can have similar physical properties. But generations of physicists have argued that this should not be the case for particle fluctuations in a BEC [2]. Specifically, when a BEC can exchange both heat and particles with a thermal reservoir—conditions described as a “grand-canonical ensemble”—theorists have predicted a fluctuation “catastrophe,” in which the fluctuations in the number of particles are as large as the total number of particles in the condensate. In contrast, under “canonical ensemble” conditions, only heat (not particles) can be exchanged with a reservoir, so the total number of particles must be conserved and large fluctuations aren’t allowed. Similarly, large fluctuations shouldn’t occur in a “microcanonical” ensemble, in which both energy and particle number are conserved.

So far, experimentalists haven’t seen these ensemble-dependent statistical effects in BECs. One reason is practical: in the case of an atom BEC, the atomic gas has to be isolated from its environment in order to cool it to low temperatures. These BECs are therefore usually prepared in microcanonical ensemble conditions [2]. In principle, it should be possible to see particle fluctuations in the BECs of exciton-polaritons [3] that can occur in solid-state systems. But both the accurate control of the reservoir and a precise measurement of the fast (picosecond-scale) fluctuations have proven difficult. Finally, theoretical work has questioned if it is possible for a BEC to form under grand-canonical ensemble conditions [4].

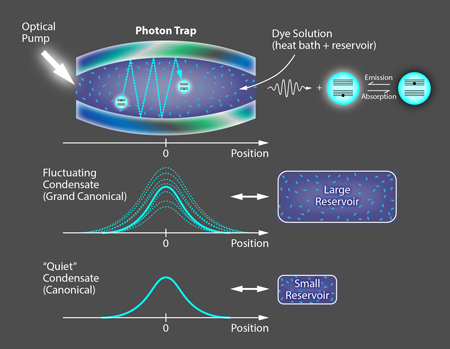
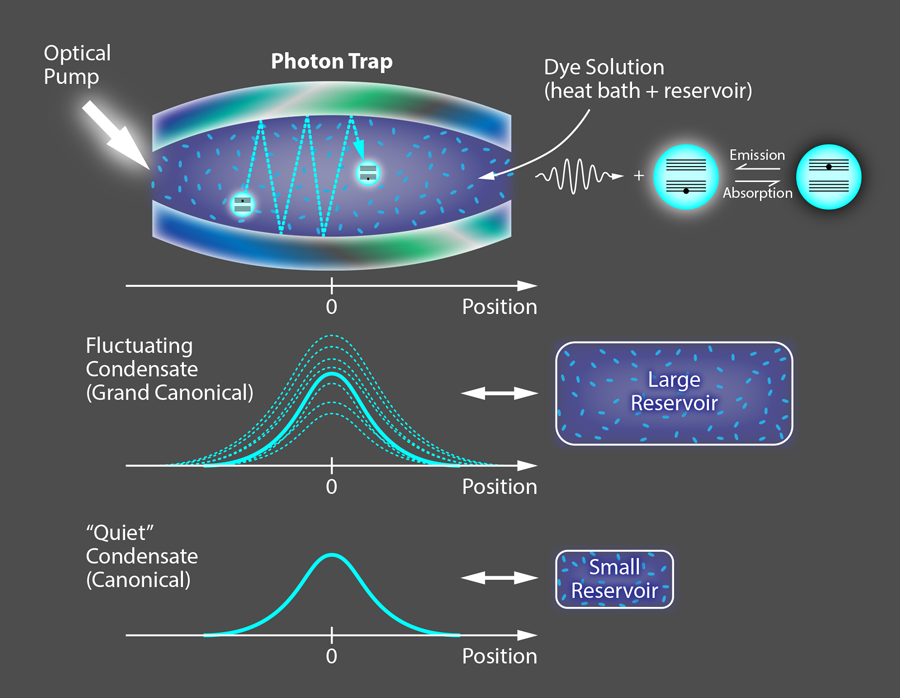
The Bonn group shows that, in fact, these conditions are possible in a BEC of photons, a system they first produced several years ago [5]. In their setup, they generate photons by using a laser to excite dye molecules within an optical cavity with a mirror on both ends (Fig. 1, top). If these two mirrors were perfectly flat, only the motion of the photons in the longitudinal direction (perpendicular to the mirrors) would be quantized, and the photons would be free to move in the transverse direction—behavior that is equivalent to the photons having an effective mass. But the mirrors in Schmitt et al.’s setup are slightly curved, which provides further confinement and also quantizes the transverse motion of the photons. As a result, the trapped photons behave as a two-dimensional gas of massive bosons in a harmonic potential. The dye molecules in Schmitt et al.’s experiment have been carefully chosen so that, when excited, they emit photons with energies similar to the sublevels in a particular longitudinal cavity mode (in this case, $\sim 2.1$ electron volts). To form a BEC, the de Broglie wavelengths of bosons must have substantial overlap, which for atoms only occurs at submicrokelvin temperatures. But the effective mass of the cavity photons in Schmitt et al.’s experiment is many orders of magnitude smaller than that of a hydrogen atom, allowing the photon BEC to form at room temperature.

In this setup, the molecules in the cavity can both absorb and emit photons, and therefore act as both a particle reservoir and a heat bath. The Bonn group uses a so-called Hanbury-Brown-Twiss setup to measure the average fluctuation $δ n_{0}$ around the mean number $n_{0}$ of condensed photons. The researchers can alter the type of reservoir—and hence the statistical ensemble conditions—by tuning the number of dye molecules and altering their chemical composition to change their transition frequency. In fact, the researchers can decrease the thermal coupling between the photons in the cavity and the reservoir by increasing the difference between the dye transition frequency and the cavity mode frequency. These control parameters allow them to modify the effective size of the reservoir by over three orders of magnitude. The influence of the reservoir size on the fluctuation properties can be spectacular: When $30 %$ of the total photons in the cavity are in the condensate, and the reservoir is at its largest, the research team observes a relative fluctuation number $\frac{δ n_{0}}{n_{0}} ≃ 80 %$ (Fig. 1, center). This unusually large “flickering” is to be expected for the so-called grand-canonical fluctuation catastrophe. Yet, if they reduce the reservoir size, for the same condensate fraction, the relative fluctuation number $δ n_{0}$ / $n_{0}$ gradually approaches $0$ (Fig. 1, bottom).

Schmitt et al. have found that the photon counting distribution in their system for arbitrary reservoir size agrees with a simple statistical model. A key assumption of this statistical model [6] is that the number of optically excited molecules (i.e., the number of photons in the reservoir) plus the number of photons in the cavity is constant in the steady-state regime. For this to be true, the nonradiative decay of molecular excitations in the dye solution has to be low, as it is in Schmitt et al.’s experiment. For a large enough reservoir (one quadratically larger than the condensate), grand-canonical ensemble statistics is obtained both in the experiments and in the theory.

Whether it is possible to make photons form a true BEC has been the source of some debate. The reason is that even when the mirrors in an optical cavity are highly reflective, photons have a finite lifetime. To compensate for this loss, Schmitt et al. need to continuously excite new photons in their experiments. At first glance, it would seem a continuously pumped system can never reach thermal equilibrium, an issue that has been discussed at length in the literature on photon lasing and condensation [7–9]. But a recent nonequilibrium theory [9] has shown that, at least for dye systems such as the one studied by Schmitt et al., increasing the cavity photon lifetime allows a thermalized, Bose-Einstein-like condensation of photons to form. The key point is that the photons can reach thermal equilibrium with the vibrational temperature of the dye molecules through repeated photon absorption and re-emission. As long as these processes occur faster than the time it takes a photon in the cavity to decay, thermal equilibrium can be reached.

Schmitt et al. have essentially performed “reservoir engineering”: they have devised a laboratory system that allows them to master the fluctuations of a Bose-Einstein condensate. The physics of their system could apply to other many-body systems, such as exciton-polariton condensates in semiconductors, and could be helpful for understanding nonequilibrium situations with nonthermal statistics. One interesting path to pursue in the future would be to see how interactions between the photons in the cavity affect the statistical properties of the photon BEC. In particular, these effects may be related to the superfluid propagation of light and to the physics of strongly correlated photonic systems [10].

References

Julian Schmitt, Tobias Damm, David Dung, Frank Vewinger, Jan Klaers, and Martin Weitz, “Observation of Grand-Canonical Number Statistics in a Photon Bose-Einstein Condensate,” Phys. Rev. Lett. 112, 030401 (2014)
For a comprehensive review with historic insights, see V. V. Kocharovsky, V. V. Kocharovsky, M. Holthaus, C. H. R. Ooi, A. Svidzinsky, W. Ketterle, and M. O. Scully, “Fluctuations in Ideal and Interacting Bose-Einstein Condensates: From the Laser Phase Transition Analogy to Squeezed States and Bogoliubov Quasiparticles,” Adv. At. Mol. Opt. Phys. 53, 291 (2006)
J. Kasprzak et al., “Bose-Einstein Condensation of Exciton Polaritons,” Nature 443, 409 (2006)
R. M. Ziff, G. E. Uhlenbeck, and M. Kac, “The Ideal Bose-Einstein Gas, Revisited,” Phys. Rep. 32, 169 (1977)
J. Klaers, J. Schmitt, F. Vewinger, and M. Weitz, “Bose-Einstein Condensation of Photons in an Optical Microcavity,” Nature 468, 545 (2010)
J. Klaers, J. Schmitt, T. Damm, F. Vewinger, and M. Weitz, “Statistical Physics of Bose-Einstein-Condensed Light in a Dye Microcavity,” Phys. Rev. Lett. 108, 160403 (2012)
D. Bajoni, P. Senellart, A. Lemaître, and J. Bloch, “Photon Lasing in a GaAs Microcavity: Similarities with a Polariton Condensate,” Phys. Rev. B 76, 201305 (2007)
B. Fischer and R. Weill, “When Does Single-Mode Lasing Become a Condensation Phenomenon?” Opt. Express 20, 26704 (2012)
P. Kirton and J. Keeling, “Nonequilibrium Model of Photon Condensation,” Phys. Rev. Lett. 111, 100404 (2013)
I. Carusotto and C. Ciuti, “Quantum Fluids of Light,” Rev. Mod. Phys. 85, 299 (2013)

About the Author

Cristiano Ciuti graduated from Scuola Normale Superiore in Pisa, Italy, in 1997 and received his Ph.D. at the Swiss Federal Institute of Technology, Lausanne in 2001. He worked as a postdoc at the University of California, San Diego, and then in 2003 he became a lecturer at Ecole Normale Supérieure, Paris, France. Since 2006 he has been a professor at Université Paris Diderot, where his research group studies the theory of strongly correlated photonic (polaritonic) systems, nonequilibrium quantum fluids, and (ultra)strong coupling cavity QED with solid-state systems. His web site can be found here