Sending Messages with a Quantum Seal

Hermann Kampermann

Viewpoint

Sending Messages with a Quantum Seal

Institute for Theoretical Physics III, Heinrich-Heine-University Düsseldorf, Germany

July 21, 2014• Physics 7, 78

With a simple optical experiment, researchers have demonstrated a quantum digital signature scheme for identifying the sender of an electronic message without requiring the use of quantum memories.

Figure caption — **Figure 1:** In a quantum digital signature protocol, the sender Alice generates a private key $P_{k}$ and a corresponding public key $| Q_{k} 〉$ , which is a sequence of coherent states (laser pulses) drawn from a set of four nonorthogonal states: $| a 〉, | b 〉, | c 〉, | d 〉$ . Bob and Charlie each receive a copy of $| Q_{k} 〉$ that they send into a shared symmetrization station, which checks that the copies are identical (and therefore can’t be repudiated). At the same time, the recipients take a symmetrized version of $| Q_{k} 〉$ and each perform unambiguous state elimination measurements that test whether a state in the sequence is not $| a 〉$ , not $| b 〉$ , etc. They obtain partial information about the key (identified positions are denoted by a, b, c, d, unidentified cases by ?). After this initial distribution stage, Alice sends a message to Bob signed with the private key, e.g., ( $0$ ; $P_{0}$ ). Bob compares the signature to the partial information he obtained from his elimination measurements. If the match is good enough, he accepts the signature and forwards ( $0$ ; $P_{0}$ ) to Charlie who does the same comparison.

In today’s information society, the transfer, processing, and protection of information has become an essential part of our daily lives. In many cases, a recipient must confirm the origin of a message, and this usually relies on a so-called digital signature, which is a secret code sent along with the message that identifies the sender. To guard against forgery, classical digital signature schemes rely on computationally intractable problems, like factoring extremely large numbers, but there’s no proof that these codes couldn’t be cracked. Quantum digital signatures (QDS) [1] could offer unconditional security by using quantum states that cannot be fully characterized by someone hoping to forge a signature. The price to pay for going quantum is that these quantum states are fragile and thus short-lived. Previous QDS schemes required using quantum memories, which are currently not robust enough. However, another scheme has recently been proposed that directly measures—rather than stores—quantum states in order to obtain partial information about them [2]. Reporting in Physical Review Letters, Robert Collins of Heriot-Watt University, UK, and his colleagues have successfully implemented a variant of this memory-free QDS protocol in an optical system [3].

A digital signature is like a written signature in that it should be easily identified but not easily reproduced. In a simple example, Alice sends a plain text message “Meet me at 6 o’clock” to Bob and Charlie, and she signs it with some code, say Xa6OO. Only Alice would know the algorithm, or “private key,” for generating this code. However, she would share a function or protocol that would allow anyone to validate that it’s her signature (i.e., that the code and message match in some way). This system has to meet two security criteria. First, it must protect against someone deciphering the private key and then writing fake messages with a forged Alice signature. Second, a digital signature scheme has to be secure against repudiation, i.e., all recipients of a message-signature pair must come to the same conclusion—either that the signature is valid or that it is not valid.

In a rudimentary classical digital signature scheme [4], Alice wants to send a single bit message $k$ , so she assigns a private key code $P_{k}$ , for each possible message $k = 0$ or $k = 1$ . She then distributes a “one-way” function $f$ and a “public key” $Q_{k} = f (P_{k})$ , which all parties can use to validate her signature. When Alice later sends her message, say “0”, she signs it with $P_{0}$ , and Bob and Charlie can verify the message by calculating $f (P_{0})$ and checking it against the public key $Q_{0}$ . The principle behind the one-way function is that it is supposed to be impossible to invert $f$ and calculate the private key: $f^{- 1} (Q_{k}) = P_{k}$ . However, this computational bottleneck is not assured. Schemes based on the difficulty of factoring large numbers, for example, see Ref. [5], could be cracked by a quantum computer.

In the original quantum digital signature scheme [1], the one-way function is replaced by a mapping of the private key $P_{k}$ onto a quantum state $| Q_{k} 〉$ , which forms the public key that Alice sends to Bob and Charlie. The central concept here is that the public key state $| Q_{k} 〉$ is composed of quantum states from a set, $| a 〉, | b 〉, | c 〉$ …, that are, in general, not orthogonal. By the rules of quantum mechanics [6], i.e., unitarity and intrinsic randomness, it is not possible to make a measurement that identifies with certainty $| Q_{k} 〉$ . Instead, Bob and Charlie store the public key and wait for Alice to send a message with the private key signature, at which point they can choose specific quantum operations and measurements to perform on the stored $| Q_{k} 〉$ . These measurements give them enough information to decide whether or not the signature is valid. A variation of the above scheme was developed on the basis of coherent states in Ref. [7] and experimentally demonstrated in Ref. [8]. However, such a scheme is not practicable, since the wait time before a message arrives may be days or weeks, whereas currently available quantum memories can reliably store quantum states for, at most, tens of minutes (after which decoherence occurs).

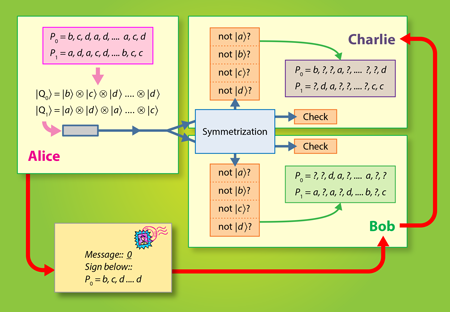
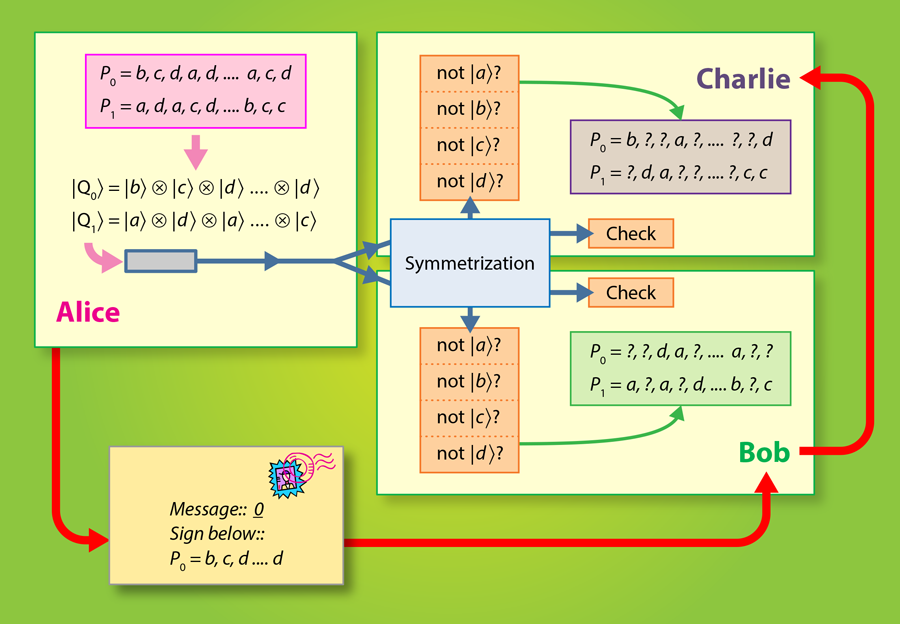
Recent work has shown that long-lasting quantum memories are not necessary in QDS [2]. Instead of storing the public key $| Q_{k} 〉$ , receiving parties measure it directly by unambiguous state discrimination or quantum state elimination measurements, and the results of these measurements (the classical data) is stored until a message is received. Again, because the public key states are nonorthogonal, only partial information about the signature key is obtained. In a proof of principle experiment [3], Collins et al. show that with current linear optics hardware, it is possible to exchange quantum digital signatures without relying on quantum memories. Here, the private key $P_{k}$ is a list of $L$ entries, where each entry is randomly chosen from four possibilities: $a$ , $b$ , $c$ , $d$ (see Fig. 1). This private key is mapped to the public key $| Q_{k} 〉$ , which is a time-ordered sequence of $L$ coherent states: $| Q_{k} 〉 = | q_{k 1} 〉 \otimes | q_{k 2} 〉 \otimes | q_{k 3} 〉 \dots \otimes | q_{k L} 〉$ . In the optical experiment of Collins et al., each $| q_{i} 〉$ is a pulse fired from a laser and then phase modulated so that its state (as determined by $P_{k}$ ) is one of four nonorthogonal states, $| a 〉, | b 〉, | c 〉, | d 〉$ . Alice sends one copy of $| Q_{k} 〉$ to Bob and another copy to Charlie. To prevent Alice from repudiating the message, both copies are sent to a symmetrization unit, which consists of a set of beam splitters that nondestructively compare Bob and Charlie’s copies. One output mode of the symmetrization unit comprises a check measurement that outputs nothing (the vacuum state) when Bob and Charlie receive identical public keys from Alice.

Following the symmetrization procedure, both Bob and Charlie perform quantum state elimination measurements on the sequence of public key states. These measurements usually only eliminate one possibility, such as $| q_{i} 〉$ is not $| c 〉$ . Still, this partial information can be used to validate a signature. When Alice later sends a message $k$ with her signature $P_{k}$ , Bob and Charlie can compare the full key to their partial (uncorrelated) information about the key. To detect a forgery or repudiation attack, the number $L$ of coherent states for each public key $| Q_{k} 〉$ must be on the order of $10^{13}$ , but the authors have identified some future improvements that could reduce this number. Also this scheme straightforwardly generalizes to any number of verifying parties, but this further increases the technical demand. The level of security of the protocol depends on the number $L$ , the errors and imperfections in the measurements, imperfections in the state preparations, losses in the quantum channel, as well as on the overlap, e.g., $| 〈 a | b 〉 |$ , between the coherent states in the set.

This latest QDS scheme is a starting point to achieve the long-term goal of practically useful quantum digital signatures. However, several theoretical and practical items can still be addressed. The security of this scheme is proven for individual as well as for collective quantum attacks, but for a universal quantum-mechanical manipulation—a so-called coherent attack—security is not yet proven. To lift these limitations, it could be promising to develop a discrete formulation in which the coherent states are replaced by single photon qubit states, as in the quantum cryptographic BB84 protocol [9]. This may allow us to adopt the exhaustive tools of finite secret key analysis [10], which could prove unconditional security in general. As a practical matter, photon losses may become significant when sending quantum digital signatures over large distances. For such situations, repeater stations might be deployed in analogy to the case of quantum key distribution. It is fascinating to see that recent developments have promoted quantum digital signature schemes from a practically impossible model to the level of complexity similar to quantum key distribution.

References

D. Gottesman and I. Chuang, “Quantum Digital Signatures,” arXiv:quant-ph/0105032v2 (2001)
V. Dunjko, P. Wallden, and E. Andersson, “Quantum Digital Signatures without Quantum Memory,” Phys. Rev. Lett. 112, 040502 (2014)
Robert J. Collins, Ross J. Donaldson, Vedran Dunjko, Petros Wallden, Patrick J. Clarke, Erika Andersson, John Jeffers, and Gerald S. Buller, “Realization of Quantum Digital Signatures without the Requirement of Quantum Memory,” Phys. Rev. Lett. 113, 040502 (2014)
L. Lamport, ”Constructing Digital Signatures from a One-Way Function,” Technical Report CSL-98, SRI International (1979)
R. L. Rivest, A. Shamir, and L. Adelman, “A Method of Obtaining Digital Signatures and Public-Key Cryptosystems,” Comm. Assoc. Comput. Mach. 21, 120 (1978)
W. Wootters and W. Zurek, “A Single Quantum Cannot Be Cloned,” Nature 299, 802 (1982)
E. Andersson, M. Curty, and I. Jex, “Experimentally Realizable Quantum Comparison of Coherent States and its Applications,” Phys. Rev. A 74, 022304 (2006)
P. J. Clarke, R. J. Collins, V. Dunjko, E. Andersson, J. Jeffers, and G. Buller, “Experimental Demonstration of Quantum Digital Signatures Using Phase-Encoded Coherent States of Light,” Nat. Commun. 3, 1174 (2012)
C. Bennett and G. Brassard, “Quantum Cryptography: Public Key Distribution and Coin Tossing,” in Proceedings of IEEE International Conference on Computers, Systems and Signal Processing (IEEE, New York, 1984)
R. Renner, “Security of Quantum Key Distribution,” Int. J. Quantum Inf. 6, 1 (2008)

About the Author

Hermann Kampermann is a private lecturer at the Heinrich-Heine-University of Düsseldorf, Germany. His research focuses on quantum cryptography, quantum repeater protocols and its security analysis, as well as on entanglement detection and its characterization. He received his doctoral degree in physical chemistry from the University of Duisburg-Essen, Germany, in 2004. Afterwards he was a postdoc in the “quantum information” graduate school at the University of Dortmund, Germany. Since the end of 2004 he has been a member of the research group of Dagmar Bruß at the University of Düsseldorf.