Victory for the Quantum Code Maker?

Roger Colbeck

Viewpoint

Victory for the Quantum Code Maker?

Department of Mathematics, University of York, York YO10 5DD, United Kingdom

September 29, 2014• Physics 7, 99

To fend off potential hackers, researchers have taken a theoretical step closer to realizing a device-independent quantum cryptography protocol.

Figure caption — **Figure 1:** In quantum key distribution, entangled states (represented as red particles) are shared between two parties, Alice and Bob, who each have a device for measuring their states. A device-independent protocol assumes nothing about these devices, treating them as “black boxes” that simply receive an input string (that controls some measurement parameter) and generate an output string (that reports the measurement outcome). Alice and Bob use their input-output data to generate a key. However, an eavesdropper, Eve, could infiltrate the system and establish entanglement with Alice and Bob’s entangled states, thereby gaining some information about the device measurements. To protect against this, Alice and Bob check that their devices violate a Bell inequality. A new security proof derives a trade-off between how close this violation is to maximum and the amount of key that can be generated.

Humans have used cryptography for more than two centuries. While the first cyphers were fairly-easy-to-crack letter swapping codes, cryptographic protocols have improved over the years, and today their use for securing bank transactions and other sensitive data is widespread. However, the schemes being used today are, in principle, breakable and the privacy of our data relies on the presumed difficulty of performing the breaking algorithm in a reasonable time. This is the best we could hope for in a world governed by classical physics. But our world obeys quantum physics, whose principles allow for verifiably secure message transmission. In the last $15$ years we have seen the development of protocols that promise an even stronger notion of security still, under the name of device independence. To date, device-independent schemes have suffered from practical drawbacks, such as low noise tolerance, or needing unrealistically many devices. Umesh Vazirani of the University of California, Berkeley, and Thomas Vidick of the California Institute of Technology, Pasadena, achieve a significant milestone by demonstrating theoretically how to remove these disadvantages, while still maintaining full security [1].

Quantum key distribution (QKD) is a method for sharing a secret key between two remote parties, Alice and Bob. If successful, then the key can serve as an encryption code, or so-called one-time pad, for fundamentally secure communication. Proofs that these protocols are secure assume a particular model of the devices being used. Such modeling is usually done in a relatively crude way and falls short of capturing the complete physics. Any mismatch between the model and the real devices represents an opportunity that can be potentially exploited by an eavesdropper. Thus, while the protocols themselves are secure, their implementation may not be, and recent hacking attacks of commercial quantum cryptography systems have exploited such weaknesses, for example, by shining bright light at certain detectors, enabling an attacker to force a certain outcome [2].

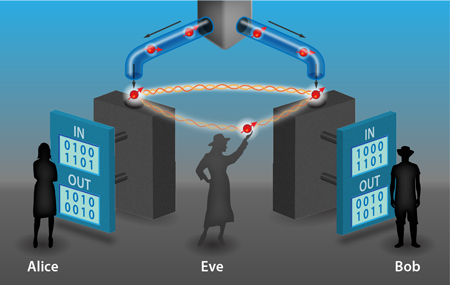
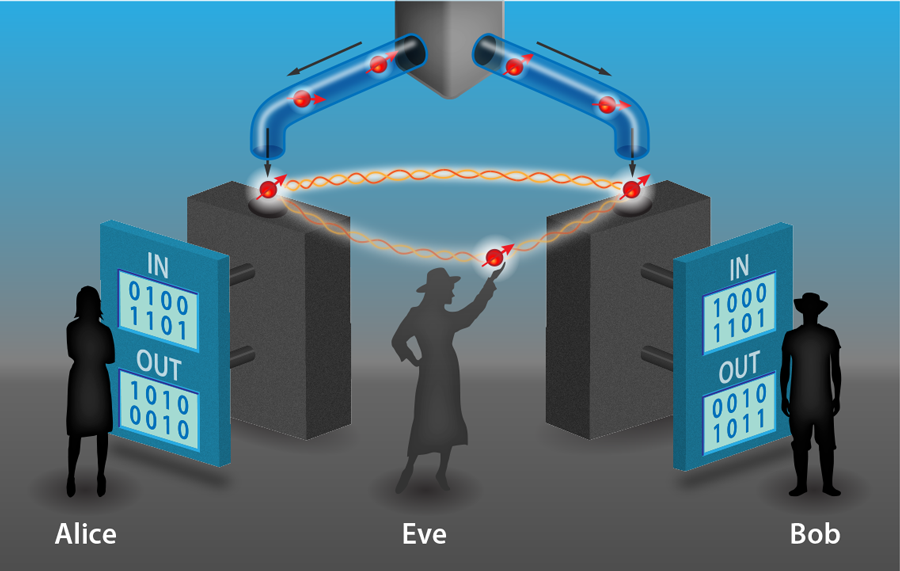
While known faults can be patched, others may remain lurking in the background, awaiting discovery by a would-be hacker. Device independence gives us a way to break free from the “hack-and-patch” cycle. In a device-independent protocol, security is no longer based on a modeling of the devices and is instead based on tests of their input-output behavior (see Fig.1). Nothing about how the devices generate their outputs need be known, except that they obey the laws of physics. Since nothing about them is assumed, there can be no mismatch between the way the real devices operate and how they are modeled in the security proof. This shuts out a wide range of attacks. In addition, device independence offers a further significant advantage: the process of checking for attacks can also identify subtle device failures—due to temperature fluctuations or component misalignment, for example—that may have gone unnoticed. The system automatically “self-tests” its performance through the device-independent protocol.

In fact, self-testing was the first name given to the concept of device independence when it was introduced in 1998 [3]. It was not until 2005 that the first provably secure device-independent protocol appeared [4]. This proof-of-principle demonstration was an important milestone, but it had three significant disadvantages: it required a large number of measurement devices, had a vanishing key generation rate, and was not robust against noise. In response, researchers have devised many alternative protocols that address one or more of the identified shortcomings [5–7] but sometimes at the expense of not treating the most general type of attack [8]. The significance of Vazirani and Vidick’s work [1] is that it eliminates these three disadvantages simultaneously, while achieving full security.

How is this achieved? At first sight, it might seem too much to ask that we can ensure security without assuming anything about how the devices are operating. However, the essential idea, the seeds of which go back over $20$ years to an early QKD scheme [9], is that if the devices held by Alice and Bob violate a Bell inequality (which can be checked directly by analyzing correlations in their input-output behavior), then they cannot be operating according to a preprogrammed deterministic strategy. In other words, their outputs must contain some randomness that is impossible for an eavesdropper, Eve, to perfectly know, even if she herself manufactured the devices Alice and Bob use.

In more detail, the violation of a Bell inequality certifies that the devices must have generated their outcomes by measurements on shared entangled states, and the higher the violation, the more entangled those states must be. However, there exists a maximum value for the violation, which corresponds to maximum entanglement. If Alice and Bob’s states are maximally entangled, then they are monogamous in the sense that they cannot be entangled with any other states. More generally, without maximal entanglement Eve can infiltrate the setup such that she holds a system that is entangled with the system measured by Alice’s device, and the more entangled Eve’s system is with Alice’s, the better she can predict Alice’s outcome. Therefore, to prevent Eve from obtaining information about the key, Alice and Bob can verify that their input-output data maximally violates a Bell inequality.

Noise and imperfections in the devices mean that Alice and Bob will not be able to observe correlations that maximally violate a Bell inequality. Thus, Vazirani and Vidick had to show that the above idea is robust in the sense that small deviations from maximal violation can, in the worst case, give an eavesdropper only a small amount of information about the raw key. Deriving this trade-off is not an easy task: Eve knows the protocol Alice and Bob will use, and she—in her role as a dishonest device manufacturer—can try to construct a system that allows her to extract critical information while avoiding detection by Alice and Bob. Unlike many previous security proofs, Vazirani and Vidick allow for the possibility that Eve programs the devices to behave differently depending on previous measurements, in order to potentially gain more information. And they also assume that Eve is able to hear all the classical information exchanged by Alice and Bob during the protocol, which further enhances her knowledge. Within this framework, the authors use fundamental quantum-mechanical principles to bound the amount of information Eve could learn about the raw key. They then use a standard technique called privacy amplification to generate a smaller key about which Eve is completely ignorant.

So is this victory for the code maker? Well, not quite yet. In order to prevent an eavesdropper exploiting inefficiencies in the detectors to her advantage (through the so-called detection loophole), a device-independent protocol has to abort if the number of missed detections is too high, and in the case of Vazirani and Vidick’s protocol, a noise rate under $2 %$ is required in order to achieve a reasonable key rate. Current experimental setups are unable to meet this requirement when Alice and Bob are separated by reasonable distances. Thus, although this is a success for the theoretical code maker, it will likely be several years before experimentalists can share in it. Indeed, in order to bring these ideas closer to being experimentally realizable, and to counter a further theoretical weakness of full device independence [10], it could be that weaker notions related to device independence take center stage, at least for the time being. These would restore trust in some aspects of the quantum devices, while others remain untrusted. Provided there is a straightforward and convincing way to verify the assumptions needed of the trusted elements, this would be a promising way forward.

This research is published in Physical Review Letters.

References

Umesh Vazirani and Thomas Vidick, “Fully Device-Independent Quantum Key Distribution,” Phys. Rev. Lett. 113, 140501 (2014)
L. Lydersen, C. Wiechers, C. Wittmann, D. Elser, J. Skaar, and V. Makarov, “Hacking Commercial Quantum Cryptography Systems by Tailored Bright Illumination,” Nature Photon. 4, 686 (2010)
D. Mayers and A. Yao, in Proceedings of the 39th Annual Symposium on Foundations of Computer Science, Palo Alto, CA, 1998 (FOCS-98) (IEEE Computer Society, Los Alamitos, 1998)[Amazon][WorldCat]
J. Barrett, L. Hardy, and A. Kent, “No Signalling and Quantum Key Distribution,” Phys. Rev. Lett. 95, 010503 (2005)
L. Masanes, R. Renner, M. Christandl, A. Winter, and J. Barrett, “Unconditional Security of Key Distribution from Causality Constraints,” arXiv:quant-ph/0606049 (2006); E. Hänggi, R. Renner, and S. Wolf, in Advances in Cryptology - EUROCRYPT 2010, Proceedings of the 29th Annual International Conference on the Theory and Applications of Cryptographic Techniques, edited by H. Gilbert (Springer, Berlin, 2010)[Amazon][WorldCat]
E. Hänggi and R. Renner, “Device-Independent Quantum Key Distribution with Commuting Measurements,” arXiv:1009.1833 (2010); L. Masanes, S. Pironio, and A. Acín, “Secure Device-Independent Quantum Key Distribution with Causally Independent Measurement Devices,” Nature Commun. 2, 238 (2011)
J. Barrett, R. Colbeck, and A. Kent, “Unconditionally Secure Device-Independent Quantum Key Distribution with Only Two Devices,” Phys. Rev. A 86, 062326 (2012); B. W. Reichardt, F. Unger, and U. Vazirani, “Classical Command Of Quantum Systems via Rigidity of CHSH Games,” arXiv:1209.0449 (2012)
A. Acín, N. Gisin, and L. Masanes, “From Bell’s Theorem to Secure Quantum Key Distribution,” Phys. Rev. Lett. 97, 120405 (2006); V. Scarani, N. Gisin, N. Brunner, L. Masanes, S. Pino, and A. Acín, “Secrecy Extraction from No-Signaling Correlations,” Phys. Rev. A 74, 042339 (2006); A. Acín, N. Brunner, N. Gisin, S. Massar, S. Pironio, and V. Scarani, “Device-Independent Security of Quantum Cryptography Against Collective Attacks,” Phys. Rev. Lett. 98, 230501 (2007)
A. K. Ekert, “Quantum Cryptography Based on Bell’s Theorem,” Phys. Rev. Lett. 67, 661 (1991)
J. Barrett, R. Colbeck, and A. Kent, “Memory Attacks on Device-Independent Quantum Cryptography,” Phys. Rev. Lett. 110, 010503 (2013)

About the Author

Roger Colbeck obtained his Ph.D. from the University of Cambridge in 2007 and then held postdoctoral positions at the Perimeter Institute, Canada, and ETH Zurich, Switzerland. In 2013 he took up a Lectureship in Mathematics at the University of York, UK. His main research interests are quantum information theory, in particular quantum cryptography, and the foundations of quantum mechanics.