Making Waves with DNA

Irving R. Epstein

Viewpoint

Making Waves with DNA

Irving R. Epstein

Department of Chemistry, MS 015, Brandeis University, Waltham, MA 02454-9110, USA

February 9, 2015• Physics 8, 12

Strands of DNA can be used to generate waves of chemical reactions with programmable shape and velocity.

Figure caption — **Figure 1:** Schematic view of the system studied by Zadorin *et al.* [1]. A single-stranded DNA (A) binds to one of the two complementary ends of the DNA template T. The resulting A:T complex uses the polymerase enzyme (*pol*) to generate another molecule of A on the template. A second enzyme (*nick*) facilitates the splitting of the two A molecules and their detachment from T. The net result is an “autocatalytic” reaction in which A catalyzes its own production: $A + T + monomers \to 2 A + T$ . By varying the concentration of DNA strands and enzymes, the authors were able to generate waves of chemical reactions with controllable shape and velocity.

Research in chemistry can be roughly divided into two categories: analysis—the measurement of existing objects and phenomena—and synthesis—the construction of those objects and phenomena from simpler pieces. Typically, synthesis lags behind analysis: one first determines the formula of a molecule (and often its structure) before attempting to make it. However, as chemistry advances, investigators are increasingly attempting to synthesize first, designing chemical systems that realize desired phenomena. A team led by André Estevez-Torres at CNRS in France and co-workers [1] has demonstrated an experimental toolkit that could be used for the rational engineering of nonlinear chemical effects in solution. Using DNA strands moving in a narrow channel and reacting under the action of enzymes, the authors are able to create chemical waves whose shapes and velocity can be finely controlled. Their setup could be programmed to yield a broad spectrum of other nonlinear phenomena in systems governed by a combination of chemical reactivity and molecular diffusion (“reaction-diffusion” systems).

Nonlinear chemical dynamics [2] characterizes many natural and industrial processes and is a quintessential feature of living organisms: most of their chemistry occurs far from equilibrium, has a nonlinear dependence on parameters like molecular concentrations, and may exhibit temporal oscillations (many biological functions are, for instance, synchronized to a 24-hour cycle). Researchers have applied a number of algorithms to design systems featuring such nonlinear behavior, engineering chemical oscillators [3] (reactions in which the concentration of one or more components exhibits periodic changes), propagating reaction fronts [4] or “Turing patterns” [5]—spatial patterns of concentrations that, as Alan Turing proposed, might be related to biological morphogenesis (e.g., the formation of leopard spots or zebra stripes).

But design algorithms are severely limited by the realities imposed by nature. One may write down a set of equations that generates a desired phenomenon, e.g., spatiotemporal chaos, for a set of reaction rates and diffusion coefficients. There is, however, no guarantee that an actual collection of molecules can be found that realizes the theorized behavior. For example, over the past several decades, researchers have successfully engineered, through systematic studies, new chemical oscillators with desired parameters for a variety of applications. These efforts have resulted in the discovery of several oscillators, but none of these oscillators “by design” has attained the importance of the Belousov-Zhabotinsky (BZ) reactions [6], a family of oscillating reactions (discovered serendipitously) that remains the most versatile and reliable chemical oscillator for most applications.

Most efforts to design reaction-diffusion phenomena have utilized small inorganic molecules, largely because these substances are cheap, easy to work with, and produce visible color changes when they undergo reduction and oxidation (redox) reactions. Unfortunately, these reaction mixtures are typically not biocompatible, and they cannot be used in applications that place them in contact with components of living systems like proteins. The BZ reaction, for example, only works at acidity levels lethal to most biological cells.

A solution may be offered by oligonucleotides (short single strands of DNA or RNA), which have been utilized as versatile building blocks for oscillators [7], computational elements [8], and structures with arbitrary shapes [9]. In their new work, Estevez-Torres et al. [1] have focused on dynamical aspects: They demonstrated that DNA strands can be used to realize an experimental model for reaction-diffusion systems whose spatiotemporal dynamics is fully controllable by programming three key elements of the system: the reaction rates, the diffusion coefficients, and the topology of the chemical reaction network (i.e., which reactions are linked to each other in ways that generate positive or negative feedback).

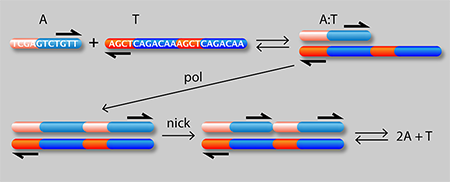
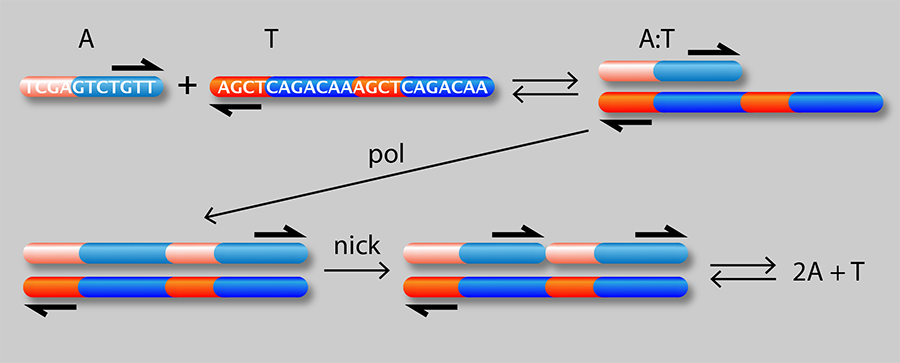
Figure 1 shows a schematic of the authors’ setup: a linear channel in which they are able to generate traveling waves of chemical concentrations whose velocity can be precisely controlled. A single strand of DNA (A) can attach to either half of a complementary strand (T) to form a complex (A:T). In the presence of an enzyme (pol), the A:T complex serves as a template for growth of an additional A strand from monomeric precursors in the solution. A second “nicking” enzyme (nick) causes the two A molecules to detach from the T strand. The net result is an “autocatalytic” reaction in which A acts as a catalyst of its own production: $A + T + monomers \to 2 A + T$

It is known [2] that autocatalytic reactions can generate chemical waves that travel with a characteristic velocity ( $ν$ ) depending on the effective rate constant ( $k$ ) for the reaction and the diffusion coefficient ( $D$ ) of the autocatalyst (A in this case): $ν = (k D)^{1 / 2}$ . This idea has been exploited [4] to generate a family of propagating acidity fronts in inorganic reactions, where the hydrogen ion ( $H^{+}$ ) was the autocatalyst. It was not possible, however, to control the velocity of those fronts, because the reaction rate depends on diffusion and the diffusion coefficient of $H^{+}$ in water is fixed. Here, the authors are instead able to tune the effective rate constant $k$ by varying the concentration of either the template or the enzyme. They can also control $D$ , the effective diffusion rate of $A$ (which depends on the diffusion rate of A relative to the A:T complex). By binding a heavy but chemically inert group C to T, they can reduce its diffusion rate and that of the complex without affecting its affinity to A. In other words, by choosing the concentrations of T, C, and pol, they can act on the two independent “control knobs” of the diffusion coefficient and the reaction rate constant. In this way, they can generate reaction waves with velocities that vary by as much as 3 orders of magnitude.

What is exciting about this approach is that it is not limited to the generation of chemical waves. The scheme could be extended to generate any desired reaction-diffusion phenomenon for which one can write a set of elementary reactions. Turing patterns, for example, could be produced, as suggested by a previous study [5], by picking a slightly different reaction network, including an activator (like A in this case) but also an inhibitor that diffuses 1 order of magnitude faster than A. The “toolbox” [10] employed by Estevez-Torres’ team, in which the activator species (A) can be slowed down by the massive inert group (C), already contains all elements needed to achieve the necessary range for diffusion coefficients.

Approaches like the one explored by the authors, building on eons of evolution in the ability to control nucleic acids, suggest a bright future for this research line. The fact that DNA-based reactions are inherently biocompatible makes them attractive for potential applications, in particular if the system can be coupled to mechanical forces, as has been done for the BZ reaction [11]. For example, one could envision inserting an anticancer drug into a DNA shell designed to undergo a mechanical deformation and release the drug when it encounters a molecule with a characteristic shape on the tumor surface.

This research is published in Physical Review Letters.

References

Anton S. Zadorin, Yannick Rondelez, Jean-Christophe Galas, and André Estevez-Torres, “Synthesis of Programmable Reaction-Diffusion Fronts Using DNA Catalyzers,” Phys. Rev. Lett. 114, 068301 (2015)
I. R. Epstein and J. A. Pojman, An Introduction to Nonlinear Chemical Dynamics: Oscillations, and Waves, Patterns and Chaos (Oxford University Press, New York, 1998)[Amazon][WorldCat]
J. Boissonade and P. De Kepper, “Transitions from Bistability to Limit Cycle Oscillations. Theoretical Analysis and Experimental Evidence in an Open Chemical System,” J. Phys. Chem. 84, 501 (1980)
L. Szirovicza, I. Nagypál, and E. Boga, “An Algorithm for the Design of Propagating Acidity Fronts,” J. Am. Chem. Soc. 111, 2842 (1989)
I. Lengyel and I. R. Epstein, “A Chemical Approach to Designing Turing Patterns in Reaction-Diffusion Systems,” Proc. Natl. Acad. Sci. U.S.A. 89, 3977 (1992)
B. P. Belousov, “A Periodic Reaction and Its Mechanism,” Sbornik Referatov po Radiatsionni Meditsine (1958) p. 145; A.M. Zhabotinsky, “Periodic Kinetics of Oxidation of Malonic Acid in Solution (Study of the Belousov Reaction Kinetics),” Biofizika, 9, 306 (1964)
M. B. Elowitz and S. Leibler, “A Synthetic Oscillatory Network of Transcriptional Regulators,” Nature 403, 335 (2000)
M. N. Stojanovic, T.E. Mitchell, and D. Stefanovic, “Deoxyribozyme-based Logic Gates,” J. Am. Chem. Soc. 124, 3555 (2002)
J. Chen and N. C. Seeman, “Synthesis from DNA of a Molecule with the Connectivity of a Cube,” Nature 350, 631 (1991)
K. Montagne, R. Plasson, Y. Sakai, T. Fujii, and Y. Rondelez, “Programming an in vitro DNA oscillator using a molecular networking strategy,” Mol. Syst. Biol. 7, 466 (2011)
R. Yoshida, T. Takahashi, T. Yamaguchi, and H. Ichijo, “Self-oscillating Gel,” J. Am. Chem. Soc. 118, 5134 (1996)

About the Author

Irving R. Epstein is Henry F. Fischbach Professor of Chemistry and Howard Hughes Medical Institute Professor at Brandeis University, where he has served as Dean of Arts and Sciences and as Provost and Senior Vice President for Academic Affairs and is currently Senior Advisor to the Provost and Senior Research Officer. He received his A.B., M.A., and Ph.D. degrees from Harvard University, a Diploma in Advanced Mathematics as a Marshall Scholar at Oxford University and was a NATO Postdoctoral Fellow at Cambridge University. He has been awarded Guggenheim and Humboldt Fellowships and was a Dreyfus Foundation Teacher-Scholar. He chaired the first Gordon Research Conference on Chemical Oscillations and Dynamic Instabilities and currently serves on the editorial boards of Chaos and the Journal of Systems Chemistry and on the boards of directors of the New England Complex Systems Institute and the Mathematical Biosciences Institute. He is a Fellow of the Massachusetts Academy of Sciences. His current research interests are in nonlinear chemical dynamics, particularly pattern formation, oscillating reactions, chaos and the behavior of complex networks.