Controlling Collisions in a Two-Electron Atomic Gas

Simon Cornish

Viewpoint

Controlling Collisions in a Two-Electron Atomic Gas

Joint Quantum Centre Durham-Newcastle, Department of Physics, Durham University, Durham DH1 3LE, United Kingdom

December 21, 2015• Physics 8, 125

Two separate groups have managed to control the interactions in a cold atomic gas in which each atom has two valence electrons.

Figure caption — **Figure 1:** Schematic of the orbital Feshbach resonance. Researchers use optical pumping and other techniques to prepare an ytterbium gas in a mixture of orbital ( $|g〉, |e〉$ ) and spin ( $|↑〉, |↓〉$ ) states. This leads to different scattering channels, like, for example, an atom in the $|g↑ 〉$ state colliding with another atom in the $|e↓ 〉$ state. For zero magnetic field (left), this “open” channel $|g↑; e ↓ 〉$ has the same long-distance energy as the “closed” channel $|g↓; e ↑ 〉$ . But for a nonzero magnetic field (right), the two channels are separated in energy by $Δ 𝜇 B$ , which can be tuned to match the binding energy $E_{c}$ of a shallow molecular bound state in the closed channel. This resonance condition produces a very large change in the atomic interaction strength.

Over twenty years have passed since the first observations of Bose-Einstein condensation in a dilute atomic gas, yet the study of ultracold gases continues to reveal fascinating insights into the quantum world. This success is driven by the ability of researchers to understand and harness subtle physical phenomena in order to exert ever-more exacting control over ultracold atoms. For example, it is becoming routine to manipulate, interrogate, and detect individual atoms confined in optical lattices. The behavior of atoms in such artificial crystals of light can mimic the physics of electrons in solids, enabling the simulation of more complex quantum systems. In this context, atoms with two valence electrons, such as strontium and ytterbium, offer new opportunities to simulate systems with many degrees of freedom, such as transition-metal oxides and spin liquids. Unfortunately, an important control technique, the ability to tune atomic collisions with a magnetic field through the use of a Feshbach resonance, was expected to be impossible in two-electron atoms. However, two groups, Simon Fölling and co-workers at the Ludwig-Maximilian University in Germany and Leonardo Fallani and colleagues at the University of Florence, Italy, have realized a novel type of Feshbach resonance that tunes the collisions between fermionic ytterbium atoms in different electronic and nuclear spin states [1, 2].

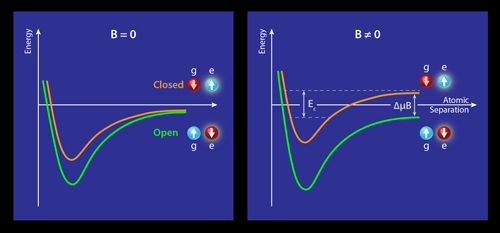
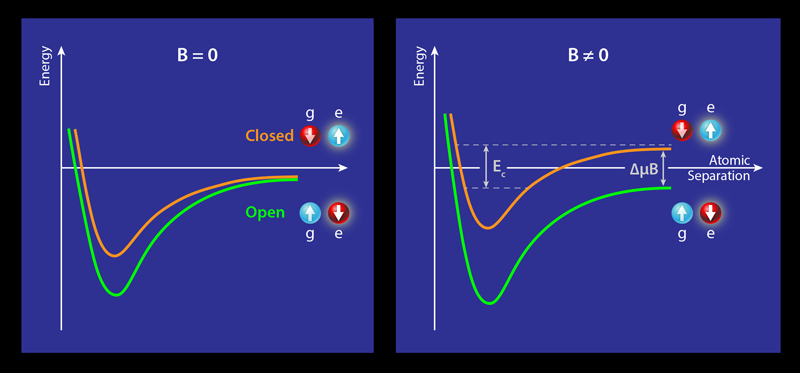
In the ultracold regime, atom-atom collisions are dominated by isotropic (s-wave) scattering. Because of this, the s-wave scattering length determines the strength and repulsive/attractive nature of atomic interactions in the gas. At a Feshbach resonance the scattering length diverges, allowing the atomic interactions to be tuned across the full range of possible values. Feshbach resonances arise when the energy of two colliding atoms matches the energy of a bound molecular state. The bound state is associated with a different molecular potential that is normally inaccessible (or closed), lying higher in energy than the colliding atoms in the entrance (or open) channel (see Fig.1, left). In alkali-metal (one-electron) atoms, the hyperfine interaction between the total spin of the unpaired valence electron and the nuclear spin provides a coupling between open and closed channels with different magnetic moments. An applied magnetic field may then be used to tune the colliding atoms into resonance with a molecular bound state. The exquisite control of the scattering length that results has made the magnetic Feshbach resonance an important tool in quantum gas experiments, enabling many scientific breakthroughs, like the realization of the BEC-BCS crossover and three-body Efimov states [3].

In contrast, alkaline-earth-type atoms with two valence electrons, such as ytterbium, have no electronic angular momentum (zero total spin) in either the singlet $^{1} S_{0}$ ground state (denoted $|g〉$ ) or the metastable triplet $^{3} P_{0}$ excited state ( $|e〉$ ). The magnetic insensitivity of these states can be a plus: the associated suppression of the hyperfine interaction makes these atoms superb candidates for a new generation of atomic clocks based upon ultranarrow optical transitions [4]. At the same time, however, these properties preclude the existence of magnetic Feshbach resonances within either of the two orbital ( $|g〉$ or $|e〉$ ) states.

However, there is another way to induce a Feshbach resonance, as shown by the groups in Munich and Florence. The teams realized a recently proposed technique referred to as an orbital Feshbach resonance [5]. Working with ultracold ytterbium ( $^{173} Yb$ ) atoms confined in an optical lattice, the researchers exploit an additional spin degree of freedom offered by ytterbium’s $I = 5 ∕ 2$ nuclear spin. Out of the multiple nuclear spin states ( $N = 6$ ), they select two of them ( $|↑〉$ and $|↓〉$ ) and then prepare the gas of atoms in a mixture of specific orbital and spin states. This leads to multiple scattering channels. In particular, when a magnetic field is applied, it is possible to identify an open channel associated with $|g↑; e ↓ 〉$ and a closed channel associated with $|g↓; e ↑ 〉$ (see Fig. 1). When the atoms are far apart, these states have an energy difference ( $Δ 𝜇 B$ ) that arises from a small difference in the nuclear Landé g-factor between the orbital states, $|g〉$ and $|e〉$ . Crucially, at short range, the correct symmetrization of the scattering states mixes the open and closed channels leading to an effective interorbital spin-exchange interaction [5], which provides the necessary coupling to the closed channel.

The final ingredient needed for the existence of a Feshbach resonance is a bound state in the closed channel within an accessible magnetic field range. Remember, however, that as both orbital states have no electronic spin, there is only limited tuning with magnetic field through the nuclear Zeeman effect (which is smaller than the electronic Zeeman effect by a factor equal to the electron to proton mass ratio $\sim 1 ∕ 1836$ ). Fortunately, recent measurements by both groups [6, 7] of the interorbital scattering properties revealed the existence of a shallow molecular bound state in the closed channel (binding energy $E_{c}$ in Fig. 1), bringing the predicted orbital Feshbach resonance within reach of the experiments.

The two groups present complementary observations of the resonance. The Munich group measures the inter-orbital thermalization rate (which is proportional to the collision cross section) in the closed channel as a function of magnetic field. From this they extract the scattering length, which reveals the characteristic dependence of a Feshbach resonance. The Florence group measures the expansion of the gas following release from the trap. For gas prepared in the open channel, they observe an anisotropic expansion when they tune the magnetic field in the vicinity of the resonance, indicating a high collision rate in the gas. Both groups identify the field where the interaction strength is the strongest (the pole) to be at around 50 gauss.

Intriguingly, the absence of electronic angular momentum in $|g〉$ and $|e〉$ with the associated decoupling of electronic and nuclear spin leads to a novel SU(N) symmetry in the collision properties of ytterbium [8]. This symmetry means that collisions between two atoms do not depend on their nuclear spin. Both groups demonstrate this by repeating their measurements using different spin states and showing that all the data collapse onto a single curve. This SU(N) symmetry, together with the long-lived clock states $|g〉$ and $|e〉$ , represents a highly controllable system in which the exchange interactions at the heart of many magnetic phenomena (such as the alignment of spins in ferromagnetism) can be studied with exquisite sensitivity. In addition, the control of two-electron atoms demonstrated by the teams of Fallani and Fölling opens new opportunities for the study of unusual forms of topological superfluids with spin-orbit coupling [5]. They also bring within reach the quantum simulation of novel spin-lattice models [9] relevant to our understanding of magnetism in strongly interacting materials.

This research is published in Physical Review Letters.

References

M. Höfer, L. Riegger, F. Scazza, C. Hofrichter, D. R. Fernandes, M. M. Parish, J. Levinsen, I. Bloch, and S. Fölling, “Observation of an Orbital Interaction-Induced Feshbach Resonance in $^{173} Yb$ ,” Phys. Rev. Lett. 115, 265302 (2015).
G. Pagano, M. Mancini, G. Cappellini, L. Livi, C. Sias, J. Catani, M. Inguscio, and L. Fallani, “Strongly Interacting Gas of Two-Electron Fermions at an Orbital Feshbach Resonance,” Phys. Rev. Lett. 115, 265301 (2015).
C. Chin, R. Grimm, P. Julienne, and E. Tiesinga, “Feshbach Resonances in Ultracold Gases,” Rev. Mod. Phys. 82, 1225 (2010).
A. D. Ludlow, M. M. Boyd, J. Ye, E. Peik, and P. O. Schmidt, “Optical Atomic Clocks,” Rev. Mod. Phys. 87, 637 (2015).
R. Zhang, Y. Cheng, H. Zhai, and P. Zhang, “Orbital Feshbach Resonance in Alkali-Earth Atoms,” Phys. Rev. Lett. 115, 135301 (2015).
F. Scazza, C. Hofrichter, M. Höfer, P. C. De Groot, I. Bloch, and S. Fölling, “Observation of Two-Orbital Spin-Exchange Interactions with Ultracold SU(N)-symmetric fermions,” Nature Phys. 10, 779 (2014).
G. Cappellini et al., “Direct Observation of Coherent Interorbital Spin-Exchange Dynamics,” Phys. Rev. Lett. 113, 120402 (2014).
S. Taie, Y. Takasu, S. Sugawa, R. Yamazaki, T. Tsujimoto, R. Murakami, and Y. Takahashi, “Realization of a SU(2) × SU(6) System of Fermions in a Cold Atomic Gas,” Phys. Rev. Lett. 105, 190401 (2010).
A. V. Gorshkov, M. Hermele, V. Gurarie, C. Xu, P. S. Julienne, J. Ye, P. Zoller, E. Demler, M. D. Lukin, and A. M. Rey, “Two-Orbital SU(N) Magnetism with Ultracold Alkaline-Earth atoms,” Nature Phys. 6, 289 (2010).

About the Author

Simon Cornish is a Professor in the Department of Physics at Durham University and a member of the Joint Quantum Centre Durham-Newcastle. He was educated at Oxford University where he received his Ph.D.in experimental atomic physics in 1998. He developed an interest in ultracold atoms while he was a Lindemann Fellow at the University of Colorado where he undertook pioneering experiments on Bose-Einstein condensation with tunable interactions. His current research interests include the study of bright matter-wave solitons, quantum degenerate mixtures, and the formation of ultracold heteronuclear molecules for applications in quantum simulation.