Electron Model Captured by Atom Pair

Adam Kaufman; Cindy Regal

Viewpoint

Electron Model Captured by Atom Pair

Adam Kaufman

University of Colorado, Boulder, CO 80309, USA

Cindy Regal

February 23, 2015• Physics 8, 16

A simple system consisting of a pair of atoms in a two-site “minicrystal” is able to reproduce the physics of a widely used model of electrons in a solid.

Figure caption — **Figure 1:** Researchers have created a simple model of electrons in a solid by capturing two atoms in a pair of optical tweezers (represented by potential wells). The team can control the interaction energy ( $U$ ) between the atoms and observe how the atoms occupy the two tweezers. For large repulsive interactions ( $U \to \infty$ ), the atoms are increasingly likely to be observed in different tweezers (Mott insulator). By contrast, large attractive interactions ( $U \to - \infty$ ) lead to atoms pairing on the same site (charge-density regime).

Understanding and creating models that explain how electrons move and interact in metals has been at the heart of theoretical and experiment efforts for nearly 100 years. One approach to probing these systems is to devise a simple mathematical model of the electrons, which pares down the complexity of the system to its most basic elements. The Fermi-Hubbard model is one such model. It reduces electron behavior to two actions: a hopping motion between sites in the metal lattice and an interaction between electrons. The hope is that, despite the model’s simplicity, it might capture observed behaviors, such as a metal’s transition to being insulating or magnetic. However, the predictions—even of a simple model—become mathematically prohibitive for large numbers of electrons. This leaves experiment as a key tool for testing theories, such as the Fermi-Hubbard model, by simulating them with real particles that are easier to control than electrons inside metals [1]. Simon Murmann and his colleagues at the University of Heidelberg, Germany, have created tunable, tailored environments in which two fermionic atoms display key components of the Fermi-Hubbard model [2].

Using ultracold neutral atoms to simulate the Fermi Hubbard model has been an ongoing endeavor over the past ten years, representing a frontier in ultracold atomic physics. Pioneering work used “optical lattices,” in which interfering beams of light create a periodic structure for ultracold atoms that mimics the crystal structure within a metal. The atoms move via quantum tunneling and interact through collisions [3]. When the interaction energy is small compared to the kinetic energy, the atoms are largely free to move around (although fermionic atoms—like electrons—cannot occupy the same lattice site unless their spins are different). The situation changes as the interaction energy between atoms is increased. The atoms spontaneously arrange themselves so that only a single atom occupies each lattice site—a spatial configuration that is called a Mott insulator because the atoms tend to stop moving in analogy to electronic motion in an insulating material. This is a key feature of the Fermi-Hubbard model and is known as the metal-Mott quantum phase transition [4,5].

In the Mott phase, the position of one atom affects that of another, but the spin of the atom at one site does not influence the spin of atoms on neighboring sites. However, at sufficiently low temperatures, a new energy scale kicks in associated with a process known as superexchange. Superexchange affects how the spins themselves order on the lattice by exacting a tiny energy cost when the atoms on nearest sites share the same spin state. Consequently, for a truly zero-temperature system, one expects the spins to form a quantum magnet in which the spins are ordered in an alternating (antialigning) pattern. Signatures of quantum magnetism in optical lattices have been observed quite recently by applying ingenious cooling techniques [6,7]. However, achieving near-zero temperatures with optical lattices has proven experimentally challenging.

Murmann et al.’s novel approach realizes an extremely low-temperature fermionic system, which they use to observe physics at superexchange energy scales. Their observations are enabled by a versatile optical tweezer platform [8,9], which can trap ultracold atoms at the beam center of a highly focused laser. They first prepared a sample of fermionic lithium atoms of opposing spin by immersing an optical tweezer in a gas of atoms, to tweeze out the coldest atoms [8]. By introducing a second optical tweezer next to the first, the researchers created a tiny two-site crystal. The atoms can “hop” from one site to the other by tunneling through the potential barrier that separates them. The researchers induced an interaction between the atoms by tuning a magnetic field that modifies the magnitude of their collision energy. As such, the system has all the features for simulating the Fermi-Hubbard model.

The dual tweezer system is uniquely tunable, allowing Murmann et al. to prepare nearly arbitrary two-atom quantum states. After selecting a particular state, the researchers varied the interaction strength and then observed how the atoms arranged inside their minicrystal. The ability to directly observe single fermions in an optical lattice has been a challenging and persistent experimental goal. Murmann et al. succeed at number- and site-resolved observation by releasing atoms from one tweezer and recapturing them in a large magnetic trap, where they can be fluorescently imaged. The group’s technique allows detailed characterization of the current two-particle system and, importantly, can be extended to larger modestly sized samples.

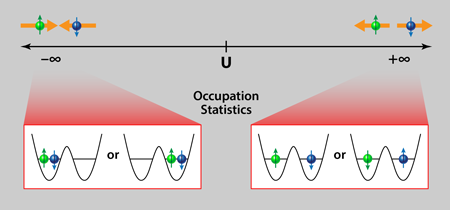
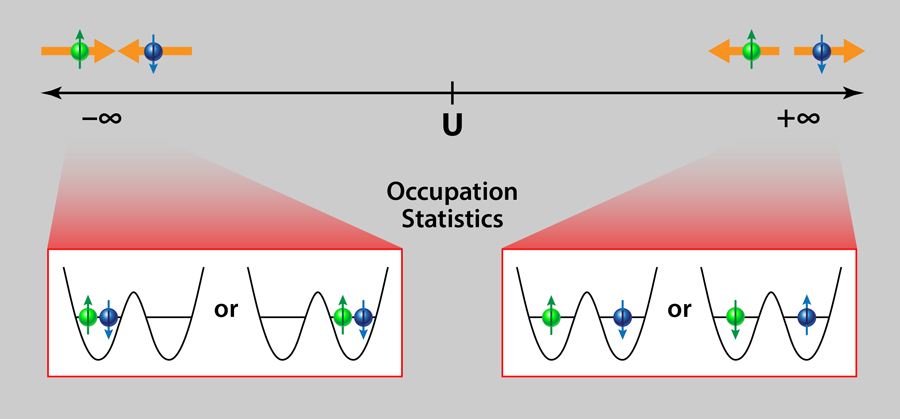
As they cranked up the repulsive interactions between the fermions, Murmann et al. observed the two-particle analog of a Mott-metal transition. When the interactions are small, the atoms either occupied the same optical tweezer or different ones, exhibiting a metal-like freedom of movement. By contrast, for strong repulsive interactions, the atoms preferred to occupy different sites, as expected for a Mott insulator (see Fig. 1). Furthermore, by tuning to attractive interactions, the researchers observed the onset of the two-particle analog of the “charge-density regime,” in which the atoms pair up to always occupy the same optical tweezer, but without preference for one site over the other.

The researchers were also able to measure the energy of the total system and how it varied with the interaction energy. They used this spectroscopic capability to compare two different excited states, whose energy difference is known to be influenced by the superexchange energy scale. They observed that the energy splitting decreased with increasing interaction energy, in beautiful correspondence to the two-site Fermi-Hubbard model prediction.

By benchmarking a platform that mirrors the physics expected for the Fermi-Hubbard model of two particles, the experimentalists can now try to scale up their system to more particles and possibly observe a variety of intriguing physical effects. They could simulate the ground state of a larger Fermi-Hubbard model by first preparing a one-dimensional chain of individual atom pairs in double wells and slowly merging them to create an ultralow entropy chain of interacting fermions. Alternatively, they could prepare a square array of four fermions to probe $d$ -wave superfluidity [10], which is believed to be a key ingredient in high-temperature superconductors. Ultimately, a variety of interesting physics inside and outside of the Fermi-Hubbard model can be experimentally investigated, depending on how the experimentalists choose to put together their fermions.

This research is published in Physical Review Letters.

References

R. Feynman, “Simulating Physics with Computers,” Int. J. Theor. Phys. 21, 467 (1982)
Simon Murmann, Andrea Bergschneider, Vincent M. Klinkhamer, Gerhard Zürn, Thomas Lompe, and Selim Jochim, “Two Fermions in a Double Well: Exploring a Fundamental Building Block of the Hubbard Model,” Phys. Rev. Lett. 114, 080402 (2015)
M. Greiner, O. Mandel, T. Esslinger, T. W. Hänsch, and I. Bloch, “Quantum Phase Transition from a Superfluid to a Mott Insulator in a Gas of Ultracold Atoms,” Nature 415, 39 (2002)
R. Jördens, N. Strohmaier, K. Günter, H. Moritz, and T. Esslinger, “A Mott Insulator of Fermionic Atoms in an Optical Lattice,” Nature 455, 204 (2008)
U. Schneider, L. Hackermüller, S. Will, T. Best, I. Bloch, T. A. Costi, R. W. Helmes, D. Rasch, and A. Rosch, “Metallic and Insulating Phases of Repulsively Interacting Fermions in a 3D Optical Lattice,” Science 322, 1520 (2008)
D. Greif, T. Uehlinger, G. Jotzu, L. Tarruell, and T. Esslinger, “Short-Range Quantum Magnetism of Ultracold Fermions in an Optical Lattice,” Science 340, 1307 (2013)
Hart et al., “Observation of Antiferromagnetic Correlations in the Hubbard Model with Ultracold Atoms,”arXiv:1407.5932v2
F. Serwane, G. Zürn, T. Lompe, T. B. Ottenstein, A. N. Wenz, and S. Jochim, “Deterministic Preparation of a Tunable Few-Fermion System,” Science 332, 336 (2011)
A. M. Kaufman, B. J. Lester, C. M. Reynolds, M. L. Wall, M. Foss-Feig, K. R. A. Hazzard, A. M. Rey, and C. A. Regal, “Two-Particle Quantum Interference in Tunnel-Coupled Optical Tweezers,” Science 345, 306 (2014)
A. M. Rey, R. Sensarma, S. Fölling, M. Greiner, E. Demler, and M. D. Lukin, “Controlled Preparation and Detection of $d$ -wave Superfluidity in Two-Dimensional Optical Superlattices,” Europhys. Lett. 87, 60001 (2009)

About the Authors

Adam Kaufman received his undergraduate degree at Amherst College and is just finishing up his Ph.D. in physics at JILA and the University of Colorado at Boulder. His Ph.D. work focused on quantum control of single atoms in optical tweezers using laser-cooling techniques, which enabled the observation of an atomic analog to the Hong-Ou-Mandel effect.

Cindy Regal is an assistant professor of physics at the University of Colorado, Boulder, where she conducts research at JILA (a joint institute between the University of Colorado and NIST). She received her Ph.D. in 2006 at JILA where she worked on ultracold Fermi gases, and she then pursued postdoctoral research at the California Institute of Technology. Her research focuses on cavity optomechanics and assembly of tailored ultracold gases.