Crystal Vibrations Invert Quantum Dot Exciton
In an atomic or molecular ensemble, population inversion is the condition in which the number of particles in an excited state exceeds that of a lower energy state. This out-of-equilibrium situation is an essential requirement for lasing and many schemes for quantum state control. Yet inverting a population is more complicated than just exciting from the lower to the higher state. Indeed, semiclassical physics tells us that a simple two-level system driven by a continuous wave (cw) laser cannot achieve steady-state population inversion. Most strategies rely on a multilevel structure, e.g., three- and four-level pumping schemes. But researchers have now developed an alternative way that utilizes crystal lattice vibrations, or phonons. John Quilter of the University of Sheffield, UK, and his colleagues have achieved population inversion in a two-level quantum dot by exploiting phonon energy levels that couple to the dot’s electronic states [1]. Like other recent works [2], the team generates phonon-assisted scattering with laser pulses, but the method has the potential to work with cw laser pumping as well. The result may enable the realization of single-exciton light sources that can be integrated into a chip, supplying single photons for applications in quantum information science.
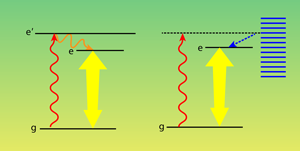
A two-level system has a ground state and an excited state. Typically, the ground state is more populated based on thermodynamic principles. One can try to pump the system from the ground state to the excited state using light that is resonant with the energy difference between the levels. However, this light will also stimulate the excited system to relax back down to the ground state, emitting a photon as it does. With a pulsed laser, one can invert the population by providing just enough light to pump the system into the excited state, but then shutting it off before the stimulated emission starts. This isn’t possible with a cw light source, in which the two competing processes are occurring simultaneously. The usual way to overcome this is to utilize a system with multiple levels. In a three-level system, for example, cw light can be used to pump the system from the ground state to its highest energy state, from which it can decay quickly into a long-lasting (metastable) intermediate energy state. Under the right conditions, the intermediate population can be greater than the ground-state population, and this inversion can be used to operate a laser (see Fig. 1).
There exist alternative ways to achieve population inversion even in a two-level system. In general, these methods rely on coupling to an auxiliary system that provides the missing additional levels. For example, researchers have shown that a steady-state inversion could be achieved for a two-level system through the effects of quantum optical noise, i.e., by coupling to a quantized cavity mode that acts as an auxiliary system [3]. A similar process can occur in semiconductor quantum dots, in which crystal phonons provide the auxiliary system.
Quantum dots have a well-defined excited state, which is characterized by the formation of an electron-hole pair (exciton). The so-called neutral exciton state is separated from the ground state by a specific resonance energy that depends on the size and make-up of the dot. It should be mentioned that dots have other excited states, but for generating single or few photons, researchers target the two-level system comprised of the ground state and lowest lying exciton state. One of the unique features of quantum dots is the coupling between excitons and longitudinal acoustic phonons (acoustic waves in which lattice atoms vibrate in the direction of wave propagation) [4]. According to several theoretical papers, population inversion of a single neutral exciton can be achieved by pumping with a cw optical driving laser, provided the laser is detuned to the blue of the resonance to exploit an efficient phonon-emission process [5–7].
Quilter et al. have designed an experiment that follows one of these recent theoretical proposals [7]. They start with a single InGaAs/GaAs quantum dot embedded in a crystal lattice, whose acoustic vibrations interact with its electronic excitations. As a result, the two-level exciton system is complemented or “dressed” by coupling to the phonon levels. The researchers utilized the phonon levels by optically pumping with laser pulses that are detuned to the blue of the dot resonance by milli-electron-volts (meV). They measured the exciton population from the electric current produced by electron-hole pairs and found that the excited state became more dominant as the strength of the pulse increased, implying that cw population inversion is possible. The largest exciton population measured was (i.e., an exciton was created with a probability of by one laser pulse).
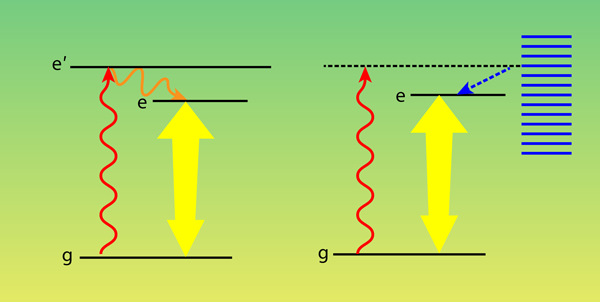
The authors describe the phonon-mediated processes through path-integral techniques. We have performed an alternative analysis using a polaron master equation, which allows one to isolate the competing processes. In this case, one first transforms the underlying energy equation to a form that nonpertubatively models a two-level system coupled to a harmonic oscillator bath. Using quantum optics techniques [6,8–10], one then identifies well-defined phonon scattering processes, the most important of which—in terms of population inversion—is phonon-assisted incoherent excitation [6,8]. In this case, a photon excites a level in the exciton-phonon band, and the absorbed energy eventually produces an exciton and a phonon. This two-step “exciton creation” process is reminiscent of the way a three-level pumping scheme populates a lower lying excited state (see Fig. 1). The reverse “exciton annihilation” process also exists: In so-called phonon-assisted radiative decay, the quantum dot absorbs a phonon, causing relaxation of the exciton (electron and hole recombine) and emission of a photon.
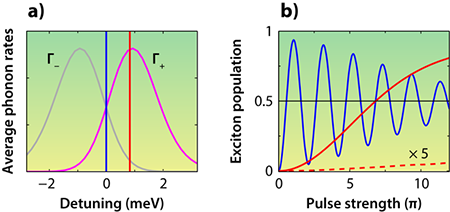
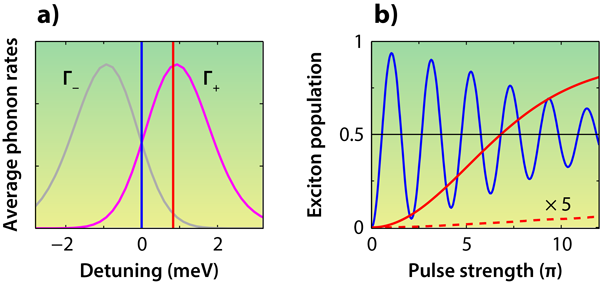
The two competing scattering rates (exciton creation and annihilation) are plotted in Fig. 2(a) as a function of detuning. The temperature in these calculations is K, which is the temperature in Quilter et al.’s experiment. The plot shows that a detuning of meV, as used in the experiment, results in a significantly higher exciton creation rate than annihilation rate. In Fig. 2(b), we plot the exciton population as a function of pulse strength, using pulse widths of around picoseconds. For a blue detuning, phonon scattering processes produce a population inversion that increases with pulse strength (replicating the results from Quilter et al.). By contrast, the exciton population for zero detuning is nonsteady, cycling up and down with pulse strength and averaging to in the cw limit. To appreciate the role that phonons play in producing a population inversion, we repeated our calculations assuming no phonon scattering and found the exciton population was near zero for a blue detuning (see Fig. 2).
The demonstrated phonon-mediated inversions are of fundamental interest in solid-state quantum optics and show that the role of phonons will likely be essential to the development and understanding of future few-photon quantum dot lasers and quantum bit architectures with quantum dot systems. In the future, single quantum dots may be placed on a chip and pumped with an off-resonant light source in order to provide on demand single photons or entangled photon pairs, which could be used for quantum cryptography and other interesting applications in quantum information processing.
This research is published in Physical Review Letters.
References
- J. H. Quilter, A. J. Brash, F. Liu, M. Glässl, A. M. Barth, V. M. Axt, A. J. Ramsay, M. S. Skolnick, and A. M. Fox, “Phonon-Assisted Population Inversion of a Single Quantum Dot by Pulsed Laser Excitation,” Phys. Rev. Lett. 114, 137401 (2015)
- P.-L. Ardelt et al. “Dissipative Preparation of the Exciton and Biexciton in Self-Assembled Quantum Dots on Picosecond Time Scales,” Phys. Rev. B 90, 241404 (2014); S. Bounouar, M. Müller, A. M. Barth, M. Glässl, V. M. Axt, and P. Michler, “Phonon-Assisted Robust and Deterministic Two-Photon Biexciton Preparation in a Quantum Dot,” arXiv:1408.7027
- C. M. Savage, “Stationary Two-Level Atomic Inversion in a Quantized Cavity Field,” Phys. Rev. Lett. 60, 1828 (1988); S. Hughes and H. J. Carmichael, “Stationary Inversion of a Two Level System Coupled to an Off-Resonant Cavity with Strong Dissipation,” 107, 193601 (2011)
- L. Besombes, K. Kheng, L. Marsal, and H. Mariette, “Acoustic Phonon Broadening Mechanism in Single Quantum Dot Emission,” Phys. Rev. B 63, 155307 (2001); A. J. Leggett, S. Chakravarty, A. T. Dorsey, M. P. A. Fisher, A. Garg, and W. Zwerger, “Dynamics of the Dissipative Two-State System,” Rev. Mod. Phys. 59, 1 (1987); S. Weiler., A. Ulhaq, S. M. Ulrich, D. Richter, M. Jetteri, P. Michler, C. Roy, and S. Hughes, “Phonon-Assisted Incoherent Excitation of a Quantum Dot and its Emission Properties,” Phys. Rev. B 86, 241304 (2012)
- T. M. Stace, A. C. Doherty, and S. D. Barrett, “Population Inversion of a Driven Two-Level System in a Structureless Bath,” Phys. Rev. Lett. 95, 106801 (2005); M. Glässl, A. Vagov, S. Lüker, D. E. Reiter, M. D. Croitoru, P. Machnikowski, V. M. Axt, and T. Kuhn, “Long-Time Dynamics and Stationary Nonequilibrium of an Optically Driven Strongly Confined Quantum Dot Coupled to Phonons,” Phys. Rev. B 84, 195311 (2011)
- S. Hughes and H. J. Carmichael, “Phonon-Mediated Population Inversion in a Semiconductor Quantum-Dot Cavity System,” New J. Phys. 15, 053039 (2013)
- M. Glässl, A. M. Barth, and V. M. Axt, “Proposed Robust and High-Fidelity Preparation of Excitons and Biexcitons in Semiconductor Quantum Dots Making Active Use of Phonons,” Phys. Rev. Lett. 110, 147401 (2013)
- C. Roy and S. Hughes, “Phonon-Dressed Mollow Triplet in the Regime of Cavity Quantum Electrodynamics: Excitation Induced Dephasing and Nonperturbative Cavity Feeding Effects,” Phys. Rev. Lett. 106, 247403 (2011); “Influence of Electron–Acoustic-Phonon Scattering on Intensity Power Broadening in a Coherently Driven Quantum-Dot Cavity System,” Phys. Rev. X 1 021009 (2011)
- H. J. Carmichael, Statistical Methods in Quantum Optics 1: Master Equations and Fokker-Planck Equations (Springer, Berlin, 2003)[Amazon][WorldCat]
- I. Wilson-Rae and A. Imamoğlu, “Quantum Dot Cavity-QED in the Presence of Strong Electron-Phonon Interactions,” Phys. Rev. B 65, 235311 (2002); D. P. S. McCutcheon and A. Nazir, “Quantum Dot Rabi Rotations Beyond the Weak Exciton-Phonon Coupling Regime,” New J. Phys. 12, 113042 (2010)