Zooming in on Entanglement

Philipp Hauke

Viewpoint

Zooming in on Entanglement

Philipp Hauke

Institute for Theoretical Physics, University of Innsbruck, A–6020 Innsbruck, Austria

July 13, 2015• Physics 8, 66

A quantum microscope images a propagating wave of entanglement between atoms trapped in an optical lattice.

Figure caption — **Figure 1:** Bloch and colleagues trap chains of ultracold rubidium atoms in an optical lattice and prepare the system in an exact eigenstate with all spins down. They then perturb it locally by flipping one spin up ( $time = 0$ ). At later times ( $time > 0$ ), the excitation propagates outwards. In a quantum mechanical medium, the resulting probability wave is a coherent superposition dominated by two entangled states, one in which the up spin has propagated to the right and one in which it has propagated to the left (less likely states are neglected for clarity). Through a quantum microscope, the authors were able to image how entanglement between individual atoms propagated as a wave up to a distance of six lattice sites.

Thanks to decades of tremendous progress in cooling and controlling clouds of atoms, laboratories around the world can now routinely create crystals of light called “optical lattices.” Generated by interfering laser beams, these structures trap atoms in periodic arrangements at ultralow temperatures, where strong quantum correlations, i.e., entanglement, can develop. The presence of entanglement makes optical lattices ideal for simulating condensed matter or particle physics systems involving large collections of strongly correlated particles, which could be too complex to investigate using classical computers. Alas, previous observations of entanglement in optical lattices have been either indirect or averaged over a macroscopic ensemble of atoms, but not on a local scale. A group led by Immanuel Bloch at the Max Planck Institute of Quantum Optics in Germany has now observed entanglement between the spins of individual atoms in an optical lattice [1]. This achievement opens the door to the microscopic characterization of strongly entangled many-body systems as well as to future uses of optical lattices in quantum information protocols.

The demonstration of Bloch and co-workers is based on a cloud of rubidium-87 atoms confined in a two-dimensional optical lattice of $9 \times 9$ sites. Two competing processes, controllable by lasers, dominate the physics of this system: The atoms can tunnel between lattice sites, and they interact when they meet at the same site. Similar setups have already been used to demonstrate the presence of entanglement, but they only obtained global averages from absorption images of the entire cloud [2]. To probe local entanglement between individual atoms, the researchers combined the optical lattice with a “quantum gas microscope,” which collects fluorescence light emitted by the atoms through a high-resolution microscope objective [3]. The microscope can not only visualize single atoms but can also manipulate them using a laser beam focused through it.

By adjusting the intensity of the laser beams generating the lattice, the researchers suppressed tunneling along one direction, effectively slicing their two-dimensional system into a collection of nine practically identical, one-dimensional chains. They loaded the optical lattice with a single atom per site, and they selected two electronic hyperfine states in each atom to form an effective spin-1/2 particle, with states “up” ( $|↑〉$ ) and “down” ( $|↓〉$ ). In the selected regime of strong atom-atom interactions, the system can be described by just the effective dynamics of these atomic spins.

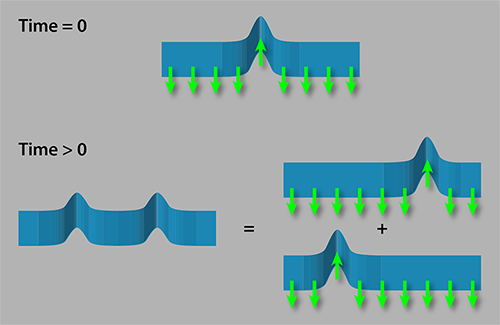
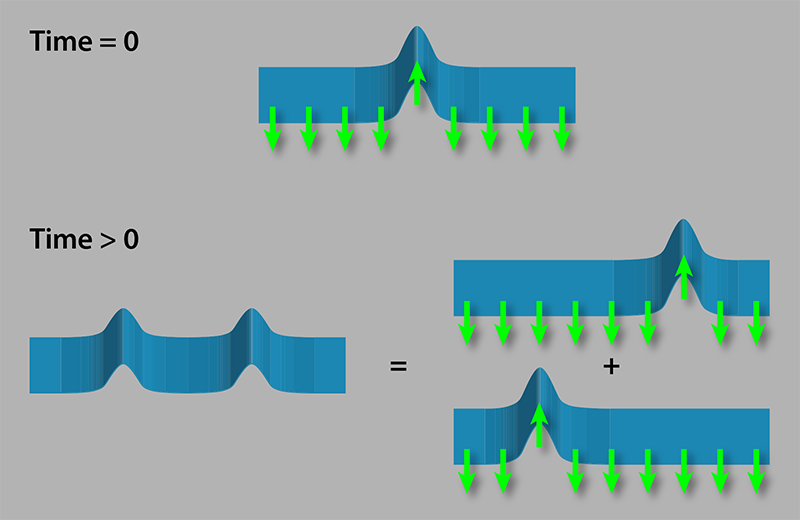
The scheme’s working principle can be illustrated through a simple analogy. Imagine throwing a pebble into a placid pond. Ripples will propagate from the impact point outwards, transporting energy and water across the surface. Similarly, by pumping all spins into $|↓〉$ , Bloch and colleagues prepare their medium in an exact eigenstate—a placid “spin pond.” Using the local control offered by the quantum gas microscope [3], the authors then perturb their quantum pond by flipping an individual spin into $|↑〉$ (see Fig. 1, top). To observe the reaction to the perturbation, the authors use an intense, resonant laser pulse to selectively push atoms with $|↓〉$ spin out of the lattice. The remaining atoms, visible through the quantum gas microscope are only those in the $|↑〉$ spin state. As in previous works, the authors observed a wave of spin-flip excitations traveling away from the perturbed site, as sketched in Fig. 1, bottom left [4, 5].

There are however, important differences with the classical pond: the quantum wave also transports quantum entanglement between different particles The wave amplitude represents the spatial distribution of the probability of finding the spin in the $|↑〉$ state. But in any single measurement, a $|↑〉$ spin is only detected at a specific position. The uncertainty in predicting where the flipped spin will be found is a manifestation of entanglement. Consider, for example, the moment when the spin-up particle had time to propagate by two lattice sites. Then, the spins at two sites to the left and two sites to the right of the center are most likely in an entangled state described by the superposition of up and down states ( $|↑, ↓〉 + |↓, ↑〉$ see Fig. 1, bottom right). While trapped-ion experiments have microscopically observed this form of entanglement [4], no optical lattice experiment had achieved this up to now.

To prove entanglement, it is not sufficient to measure the probability of finding an up spin at a given location. One would observe the same distribution from the entangled superposition $|↑, ↓〉 + |↓, ↑〉$ and from a nonentangled mixture where $|↑, ↓〉$ and $|↓, ↑〉$ randomly occur in each shot of an experiment. A strict lower bound for the amount of entanglement can, however, be reconstructed by also measuring local superpositions between $|↑〉$ and $|↓〉$ states [6]. These can be accessed using microwave pulses that rotate the spins prior to measurement. Through such measurements, the authors were able to reveal an entanglement wave, the propagation of which was observable up to a distance of six lattice sites.

Importantly, the setup could also be used to explore the detrimental effect of defects (such as lattice sites without an atom) on entanglement. In fact, the observed level of entanglement was smaller than predictions for a perfect system with exactly one atom per site. To explain the discrepancy, the authors refined their measurement technique. When blowing off atoms in the $|↓〉$ spin state, the experiments cannot distinguish between a lattice site emptied by the laser and a defect site that was empty to begin with (a “hole”). Therefore, instead of removing one of the spin states, the authors performed a so-called Stern-Gerlach spin-separation measurement which distinguishes $|↑〉$ and $|↓〉$ states by deflecting the atoms in a spin-dependent way via a magnetic field. But this refinement comes at a price: The separation requires some space perpendicular to a spin chain. As a consequence, only a single chain of nine atoms could be used in a given experiment, as opposed to a $9 \times 9$ matrix. The increased difficulty was, however, worth the price: The measurements revealed that the smaller-than-expected entanglement was due to the detrimental effect of holes. Accounting for the holes’ contribution yielded essentially perfect agreement with theory and indicated that a hole density of about 30% would completely destroy entanglement. This refined measurement strategy now makes it possible to select perfect, hole-free systems that display a large degree of entanglement.

These results open exciting prospects on two fronts. First, the coherent transport of entanglement across spin chains may enable the communication between different quantum processors or registers [7]with potential applications in quantum computing. The second aspect is the simulation of quantum phenomena. Engineered systems like optical lattices work at larger length and time scales than “natural” solid-state samples, giving researchers a much easier access to quantum many-body dynamics. Optical lattices also have a key advantage over competing solutions such as trapped ions: they are not limited to bosons or spins but can investigate fermions equally well. They can thus tackle the simulation of fundamental fermionic constituents of matter like quarks and electrons. The ability to track entanglement microscopically will be particularly useful to study effects defined through their entanglement characteristics, such as many-body localization [8]or topological quantum states [9]. It is the presence of entanglement that makes it hard for a classical computer to simulate such complex quantum many-body systems. The reported experiment is thus an important step towards understanding whether the achieved amount of entanglement will be sufficient to outperform the simulation capabilities of a classical computer [10]. If so, optical lattices may soon answer hard questions that are impossible to tackle otherwise.

This research is published in Physical Review Letters.

References

T. Fukuhara, S. Hild, J. Zeiher, P. Schauß, I. Bloch, M. Endres, and C. Gross, “Spatially Resolved Detection of a Spin-Entanglement Wave in a Bose-Hubbard Chain,” Phys. Rev. Lett. 115, 035302 (2015).
O. Mandel, M. Greiner, A. Widera, T. Rom, T. W. Hänsch, and I. Bloch, “Controlled Collisions for Multi-Particle Entanglement of Optically Trapped Atoms,” Nature 425, 937 (2003); M. Anderlini, P. J. Lee, B. L. Brown, J. Sebby-Strabley, W. D. Phillips, and J. V. Porto, “Controlled Exchange Interaction Between Pairs of Neutral Atoms in an Optical Lattice,” 448, 452 (2007); M. Cramer, A. Bernard, N. Fabbri, L. Fallani, C. Fort, S. Rosi, F. Caruso, M. Inguscio, and M. B. Plenio, “Spatial Entanglement of Bosons in Optical Lattices,” Nature Commun. 4, 2161 (2013).
W. S. Bakr, J. I. Gillen, A. Peng, S. Foelling, and M. Greiner, “Quantum Gas Microscope Detecting Single Atoms in a Hubbard Regime Optical Lattice,” Nature 462, 74 (2009); C. Weitenberg, M. Endres, J. F. Sherson, M. Cheneau, P. Schauss, T. Fukuhara, I. Bloch, and S. Kuhr, “Single-Spin Addressing in an Atomic Mott Insulator,” 471, 319 (2011).
P. Jurcevic, B. P. Lanyon, P. Hauke, C. Hempel, P. Zoller, R. Blatt, and C. F. Roos, “Observation of Entanglement Propagation in a Quantum Many-Body System,” Nature 511, 202 (2014).
M. Cheneau, P. Barmettler, D. Poletti, M. Endres, P. Schausz, T. Fukuhara, C. Gross, I. Bloch, C. Kollath, and S. Kuhr, “Light-Cone-Like Spreading of Correlations in a Quantum Many-Body System,” Nature 481, 484 (2012); T. Fukuhara, P. Schauß, M. Endres, S. Hild, M. Cheneau, I. Bloch, and C. Gross, “Microscopic Observation of Magnon Bound States and their Dynamics,” 502, 76 (2013).
L. Mazza, D. Rossini, R. Fazio, and M. Endres, “Detecting Two-Site Spin-Entanglement in Many-Body Systems with Local Particle-Number Fluctuations,” New J. Phys. 17, 013015 (2015).
S. Bose, “Quantum Communication Through Spin Chain Dynamics: An Introductory Overview,” Contemp. Phys. 48, 13 (2007).
R. Nandkishore and D. A. Huse, “Many Body Localization and Thermalization in Quantum Statistical Mechanics,” Annu. Rev. Condens. Matter Phys. 6, 15 (2015).
A. Kitaev and J. Preskill, “Topological Entanglement Entropy,” Phys. Rev. Lett. 96, 110404 (2006); M. Levin and X. G. Wen, “Detecting Topological Order in a Ground State Wave Function,” 96, 110405 (2006).
P. Hauke, F. M. Cucchietti, L. Tagliacozzo, I. Deutsch, and M. Lewenstein, “Can One Trust Quantum Simulators?,” Rep. Prog. Phys. 75, 082401 (2012); T. Johnson, S. Clark, and D. Jaksch, “What Is a Quantum Simulator?,” Eur. Phys. J. Quantum Technology 1, 10 (2014).

About the Author

Philipp Hauke is a University Assistant at the University of Innsbruck. He studied at the Technical University of Munich and the Max Planck Institute of Quantum Optics in Garching. He received his Ph.D. in 2013 from the Institute of Photonic Sciences (ICFO) and the Universitat Politècnica de Catalunya in Barcelona. His research is focused on the simulation of complex many-body phenomena in quantum optics setups. In particular, he is interested in phenomena at the interface of condensed matter, quantum optics, and quantum information, and the characterization of entanglement properties in such systems.