Uncovering a Quantum Phase Transition in Nuclei

David J. Dean

Viewpoint

Uncovering a Quantum Phase Transition in Nuclei

Physics Division, Oak Ridge National Laboratory, Oak Ridge, TN 37831, USA

September 19, 2016• Physics 9, 106

Simulations predict that the ground states of certain light nuclei lie near a quantum phase transition between a liquid-like phase and a phase involving clusters of alpha particles.

Figure caption — **Figure 1:** Lee and colleagues performed simulations of a nucleus in which they tweaked the interaction between nucleons (protons and neutrons) [1]. They found that, depending on the form of the interaction, the nucleus lay on either side of a quantum phase transition. The transition is between (left) a phase in which protons and neutrons are evenly distributed (a Fermi liquid) to (right) a phase in which the protons and neutrons cluster into alpha particles.

Thermal phase transitions surround us. Ice melts. Water boils. Triggered by thermal fluctuations, these transitions are typically characterized by a reorganization of matter at a critical temperature from one distinct phase to another. Less obvious in our everyday lives are phase transitions that occur in quantum systems at zero temperature. These quantum phase transitions exist in many condensed matter systems, in which tuning such variables as pressure, atom concentration, or magnetic field brings one quantum phase to a “critical point” with another. Instead of thermal fluctuations, these transitions are driven by the quantum fluctuations dictated by the uncertainty principle, and they often involve competing interactions (for example, repulsive versus attractive) between the phases.

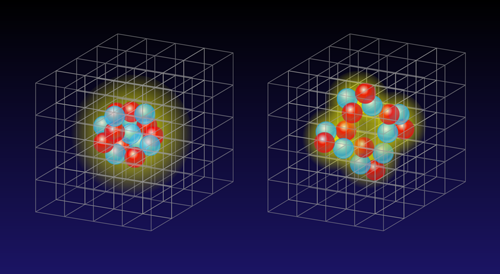
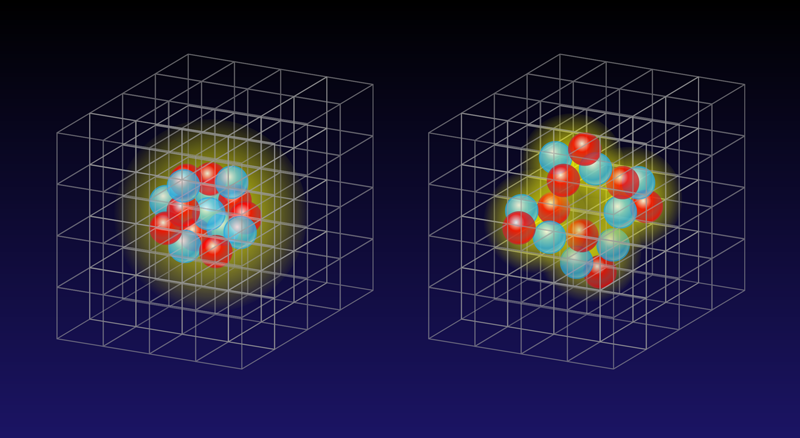
Now, theorists simulating the interactions between protons and neutrons in a nucleus have found that certain light nuclei exist near a quantum phase transition. The transition is from a state with a uniform distribution of protons and neutrons (a Fermi liquid) to a state consisting of several alpha particles (two protons and two neutrons) [1]. The finding, from Dean Lee at North Carolina State University, Raleigh, and colleagues, might provide clues as to why clustering occurs in the ground states of some nuclei but only in the excited states of others—such as the excited Hoyle state of carbon that is thought to be essential to life.

Nuclear physicists today seek to understand nuclei from the underlying interactions between protons and neutrons [2]. These interactions are described by quantum chromodynamics (QCD)—the theory of quarks and gluons—and electroweak theory. Ultimately, we would like a theoretical framework with which to predict nuclear properties, even those that are inaccessible to experiments. Thanks to modern experimental facilities, such as the Facility for Rare Isotope Beams under construction at Michigan State University, we will soon be able to test our understanding of nuclei, in particular, those that are very rich in neutrons.

In the past ten years, theorists have made tremendous progress towards describing nuclei. Propelling this effort has been the advent and application of effective field theory [3, 4]. This approach describes the nuclear force in terms of nucleons instead of the quarks and gluons that are the degrees of freedom in QCD. The Lagrangian for this nuclear force—the basis for determining the ground states and properties of nuclei—is approximated with an order-by-order series expansion, but one that preserves the symmetries of QCD. A “leading-order” expansion suffices for low-energy (long-distance) nuclear interactions, but higher-order terms are needed for high-energy (short-distance) interactions. Once the parameters of the expansion are determined, numerical techniques for solving many-body interactions, such as lattice Monte Carlo [5], can be used to describe a nucleus. These calculations have been possible thanks to steady increases in the speed and power of computers [6].

In their new work, Lee and co-workers [1] utilized a lattice Monte Carlo algorithm and a leading-order effective field theory to investigate alpha clustering in the ground state of $^{16} O$ and other similarly light nuclei with equal numbers of protons and neutrons ( $N = Z$ nuclei). Prior to this investigation, experimental and theoretical work has found evidence for clustering in light $N = Z$ nuclei in both the ground and excited states [7]. Indeed, also using lattice Monte Carlo calculations, theorists (including Lee) have shown previously that the second excited state in $^{16} O$ exhibits alpha clusters [8]. While the origin of clustering in nuclei is not fully understood, it must be rooted in nuclear interactions. In the new work, Lee and co-workers calculated the ground states of $^{16} O$ and other $N = Z$ nuclei assuming different forms of the nucleon-nucleon interaction, asking if tweaking the interaction would drive the nuclei into states exhibiting alpha clustering.

To address this question, the authors considered two possible interactions between nucleons. Both interactions are the same, except at short distances, for which the interaction cannot be described without experimentally determined parameters. The first interaction, dubbed $V_{A}$ , only includes terms that describe nonlocal short-distance interactions, meaning interactions that act over a distance instead of at a point. The second one, dubbed $V_{B}$ , includes both local and nonlocal short-distance terms, as well as extra terms that are used to properly account for the interactions between alpha particles. The researchers calculated the ground states of nuclei assuming a nucleon-nucleon interaction that interpolates between $V_{A}$ and $V_{B}$ according to a simple formula, $V (a) = (1 - a) V_{A} + a V_{B}$ , where $a$ is a parameter. Focusing on $N = Z$ nuclei ranging from $^{20} Ne$ to $^{8} Be$ , they found that at specific values of the parameter $a$ , each nucleus undergoes a phase transition from a Fermi liquid to a phase whose nucleons form alpha clusters (Fig. 1).

The authors point out that, for a given value of $a$ , a nucleus predicted to be on one side of the quantum phase transition in their leading-order calculation might be predicted to be on the other side with a higher-order calculation. This potential sensitivity to the precise nucleon-nucleon interaction is what leads the authors to suggest that “nature is near a quantum phase transition” [1].

These simulations could tell us something about real nuclei. The Hoyle state of $^{12} C$ is a particularly interesting case. This state, which plays a key role in the production of carbon in red giant stars, is created by the fusion of three alpha particles, but it is tough to calculate [9]. Knowing that nuclear ground states hover in the vicinity of a quantum phase transition might encourage experimentalists to try new ways of searching for alpha clustering in carbon and other nuclei, which is difficult to detect directly. And while clustering is most prominent in calculations of $N = Z$ nuclei, it is possible that other forms of clusters, such as neutron clusters, appear in very neutron-rich nuclei. The work from Lee and co-workers may inspire theorists to investigate these possibilities. Finding a quantum phase transition in very neutron-rich nuclei would certainly have an effect on our understanding of how nuclei bind in such systems. The future in this area is both bright and fascinating.

This research is published in Physical Review Letters.

References

S. Elhatisari et al., “Nuclear Binding Near a Quantum Phase Transition,” Phys. Rev. Lett. 117, 132501 (2016).
See, for example, A. B. Balantekin et al., “Nuclear Theory and Science of the Facility for Rare Isotope Beams,” Mod. Phys. Lett. A 29, 1430010 (2014).
E. Epelbaum, H.-W. Hammer, and U.-G. Meißner, “Modern Theory of Nuclear Forces,” Rev. Mod. Phys. 81, 1773 (2009).
A. Ekström et al., “Optimized Chiral Nucleon-Nucleon Interaction at Next-to-Next-to-Leading Order,” Phys. Rev. Lett. 110, 192502 (2013).
D. Lee, “Lattice Simulations for Few- and Many-Body Systems,” Prog. Part. Nucl. Phys. 63, 117 (2009).
Increasing computational power is documented and updated twice per year at http://www.top500.org.
W. von Oertzen, M. Freer, and Y. Kanada-En'yo, “Nuclear Clusters and Nuclear Molecules,” Phys.Rep. 432, 43 (2006).
E. Epelbaum, H. Krebs, T. A. Lähde, D. Lee, U.-G. Meißner, and G. Rupak, “Ab Initio Calculation of the Spectrum and Structure of $^{16} O$ ,” Phys. Rev. Lett. 112, 102501 (2014).
E. Epelbaum, H. Krebs, T. A. Lähde, D. Lee, and U.-G. Meißner, “Structure and Rotations of the Hoyle State,” Phys. Rev. Lett. 109, 252501 (2012).

About the Author

David J. Dean is the Physics Division Director at Oak Ridge National Laboratory. He formerly served as Senior Advisor to the Under Secretary of Science at the U.S. Department of Energy. For six years he served as a Divisional Associate Editor for Physical Review Letters. He is currently the chair of the FRIB Science Advisory Committee and the Vice Chair of the Division of Nuclear Physics of the American Physical Society. A theorist, he specializes in the application and development of techniques to solve quantum many-body problems.

Nuclear Binding Near a Quantum Phase Transition

Serdar Elhatisari, Ning Li, Alexander Rokash, Jose Manuel Alarcón, Dechuan Du, Nico Klein, Bing-nan Lu, Ulf-G. Meißner, Evgeny Epelbaum, Hermann Krebs, Timo A. Lähde, Dean Lee, and Gautam Rupak

Phys. Rev. Lett. 117, 132501 (2016)

Published September 19, 2016

Read PDF