Relaxons Heat Up Thermal Transport
Thermal transport—the flow of energy in the form of heat—is ubiquitous in engineered and natural systems. Managing it efficiently is critical for increasing the performance and lifetime of electronic circuitry, energy-conversion devices, and living organisms. In metals, heat is mainly carried by free electrons, whereas in electrically insulating solids, it is transported by atomic vibrations. Andrea Cepellotti and Nicola Marzari from the Swiss Federal Institute of Technology in Lausanne, Switzerland, now propose [1] a theoretical framework for thermal transport in crystalline electrical insulators that applies consistently to a range of two- and three-dimensional materials.
In electrically insulating, or dielectric, crystals, all atoms are at regular positions in a periodic lattice. To model thermal transport in these materials, it is convenient to change the coordinate frame from the localized positions of the individual atoms to a set of delocalized plane waves. The frequencies and other properties of these plane waves, which are called phonon modes, can be obtained from lattice dynamics calculations. In a quantum physics formulation, the phonon modes are harmonic oscillators whose energies are quantized and carried by particles—phonons—that are described by Bose-Einstein statistics.
For decades, phonons have formed the basis of our understanding of thermal transport in dielectric crystals. In these materials, thermal conductivity—which dictates how much heat will flow through an object when it is exposed to a temperature difference—results from two processes: intrinsic scattering between phonons due to atomic vibrations at finite temperature, and disruptions to the periodic lattice such as interfaces and point defects. The most common model of phonon scattering is the relaxation time approximation (RTA), which simplifies the solution of the complicated Boltzmann transport equation for thermal conductivity. Under the RTA, the phonons are imagined as particles of a gas described using kinetic theory. The population of a phonon mode perturbed from thermal equilibrium by scattering is assumed to decay, or relax, exponentially back to that of an equilibrium population comprising all other phonon modes. The decay time is called the lifetime, which can also be expressed as a length scale known as the mean free path.
The integration of density-functional-theory calculations, which provide an accurate description of the atomic interactions, of lattice dynamics theory, and of the RTA has led to predictions of thermal conductivity in dielectric crystals that agree with experimental measurements for a broad range of materials, including silicon [2]. Striking failures, however, were found for materials whose intrinsic phonon-phonon scattering is dominated by nonresistive processes, as opposed to resistive (Umklapp) processes that rule in most systems. Examples of these materials include diamond [2] and two-dimensional materials such as graphene [3]. Under this condition, the central assumption of the RTA—that perturbed phonon modes decay exponentially to an equilibrium population—is not valid. A full (non-RTA) solution of the Boltzmann transport equation is required that provides mode-dependent nonequilibrium populations, which can be used to calculate phonon-phonon scattering rates and thermal conductivity. This full solution comes at a cost, however, as the phonons no longer undergo an exponential relaxation process. As a result, their lifetimes and mean free paths are lost as descriptors of thermal transport.
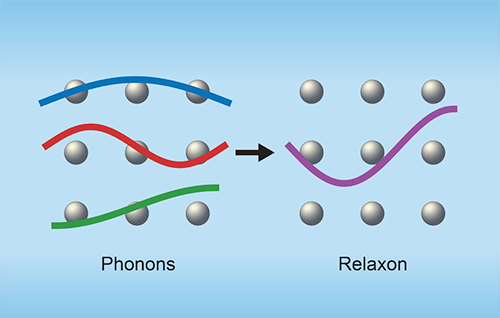
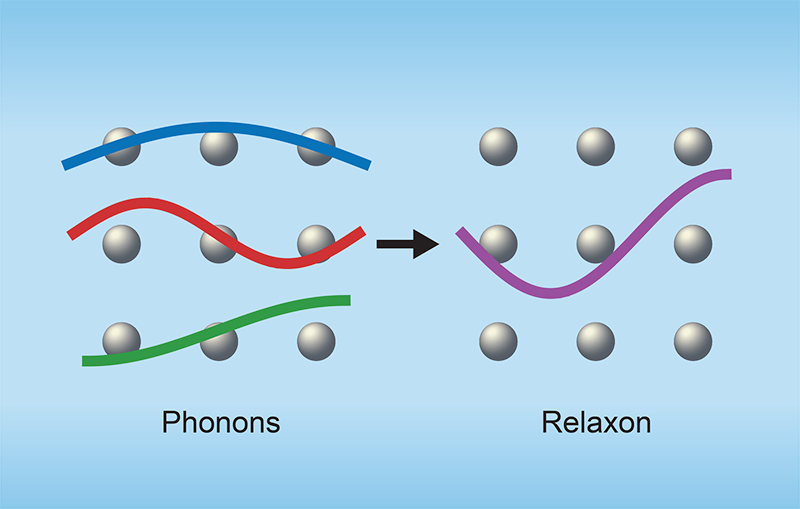
In their study, Cepellotti and Marzari reformulate the problem of thermal transport in dielectric crystals by proposing new vibrational modes called relaxons in the context of the Boltzmann transport equation. From the atomic perspective, relaxons emerge from a different coordinate-frame change than that used to obtain phonons. From the phonon perspective, each relaxon is a linear superposition of phonon modes (Fig. 1).
The relaxon picture is attractive. When perturbed, relaxons decay exponentially to an equilibrium population and have a well-defined lifetime and mean free path. A key insight provided by the relaxon theory is that it is groups of phonon modes, and not individual phonon modes, that display this relaxation behavior.
Cepellotti and Marzari apply the relaxon theory to two materials: silicon and graphene. For silicon, the RTA (phonon) and relaxon predictions of thermal conductivity are within 2% of each other. The phonon and relaxon lifetimes are in the same range (10 ps to 10 ns) and individual modes in each case make comparable contributions to thermal conductivity. These similarities demonstrate that the phonon description of thermal transport is a limit of the more general relaxon theory.
For graphene, the predictions are strikingly different, with the relaxon thermal conductivity being 8 times higher than that from the RTA. This result is in agreement with previous calculations based on a non-RTA phonon picture [3]. Also, while a broad spectrum of phonon modes contribute to thermal conductivity under the RTA, a small handful of relaxons—some of whose lifetimes exceed 50 ns—make a dominant contribution to thermal conductivity.
The relaxon theory has potential implications across theoretical and experimental studies of thermal transport. On the theoretical front, recent calculations have predicted the possibility of hydrodynamic, as opposed to diffusive or ballistic, phonon transport in graphene and other two-dimensional materials [4, 5]. This phenomenon has previously only been observed in some three-dimensional materials at extremely low temperatures, including helium and sodium fluoride. The onset of hydrodynamic transport is related to a dominance of the nonresistive processes that cause phonon-phonon scattering in these materials. Its interpretation and the design of experiments for observing it may be enabled by predictions made from the relaxon theory.
On the experimental front, the emerging field of mean free path spectroscopy [6] seeks to isolate the contributions of carriers with different mean free paths to thermal conductivity. While the lifetimes and mean free paths of phonons, and now relaxons, can be readily obtained from accurate calculations, measurements have remained a challenge. The relaxon theory will help to interpret mean free path spectroscopy measurements on diamond and two-dimensional materials.
The kinetic theory of relaxons is a re-imagination of the nature of thermal transport in dielectric crystals. The long-standing phonon picture is not dead but is a special case of a more general phenomenon. Questions now emerge, including how relaxons will scatter with point defects (such as dopant atoms), electrons, internal interfaces, and system boundaries. As Cepellotti and Marzari suggest, electrons themselves may display a relaxon-type behavior under certain conditions. Furthermore, experimentalists now have a challenge, which is how to observe relaxons and confirm their existence.
This research is published in Physical Review X.
References
- A. Cepellotti and N. Marzari, “Thermal Transport in Crystals as a Kinetic Theory of Relaxons,” Phys. Rev. X 6, 041013 (2016).
- L. Lindsay, D. A. Broido, and T. L. Reinecke, “Ab Initio Thermal Transport in Compound Semiconductors,” Phys. Rev. B 87, 165 (2013).
- L. Lindsay, W. Li, J. Carrete, N. Mingo, D. A. Broido, and T. L. Reinecke, “Phonon Thermal Transport in Strained and Unstrained Graphene from First Principles,” Phys. Rev. B 89, 155426 (2014).
- S. Lee, D. Broido, K. Esfarjani, and G. Chen, “Hydrodynamic Phonon Transport in Suspended Graphene,” Nature Commun. 6, 6290 (2015).
- A. Cepellotti, G. Fugallo, L. Paulatto, M. Lazzeri, F. Mauri, and N. Marzari, “Phonon Hydrodynamics in Two-Dimensional Materials,” Nature Commun. 6, 6400 (2015).
- K. T. Regner, J. P. Freedman, and J. A. Malen, “Advances in Studying Phonon Mean Free Path Dependent Contributions to Thermal Conductivity,” Nano. Micro. Thermophys. 19, 183 (2015).