Putting Bounds on Biochemical Noise
All processes inside a living cell are controlled by networks of biomolecules that chemically interact with each other. These interactions are fundamentally probabilistic in nature, and indeed, it is now widely recognized that biochemical networks can be highly stochastic. In addition to being noisy, these systems are often sparsely characterized and highly nonlinear. This makes it difficult, if not impossible, to make any general strong statement on their behavior. Andreas Hilfinger, from Harvard University, and his colleagues now show that it is possible to put firm bounds on the noise characteristics of biochemical networks, even when only parts of the system are known [1].
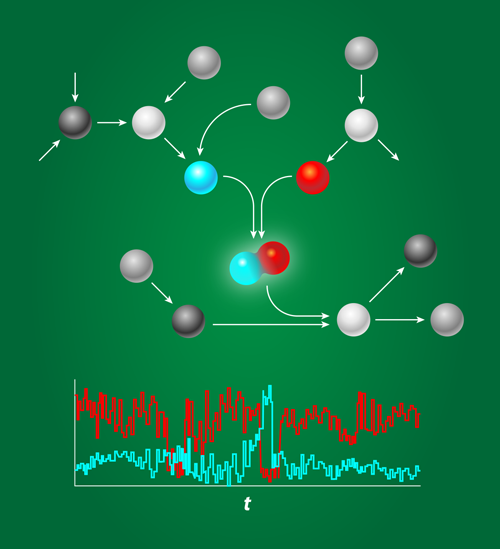
Biochemical networks are the information processing devices of life. They determine whether cells should differentiate or proliferate, stay put or move, or even continue to live or die. The components that form these networks—proteins, DNA—typically find each other by diffusion, a stochastic process. And even when they do find each other, the outcome of their interaction is also inherently probabilistic. These stochastic interactions make the system noisy (see Fig. 1) especially when the concentrations are low, as is often the case inside the cell [2]. Gene regulatory proteins, for instance, are often present in nanomolar concentrations, which, for a micrometer-sized bacterium like E. coli, correspond to just a few copies per cell. While some organisms exploit noise, for example, in hedging their response on the prospects of a changing environment, in many cases the question is how reliably cells can operate in the face of biochemical noise.
Understanding the noise characteristics of cellular systems is currently one of the key questions in biology, yet progress in answering this question has, so far, been limited. One reason is that cellular systems are incredibly complex, containing many different components that interact in a multitude of ways. High-throughput techniques in the past decade have made it possible to identify these components on an unprecedented scale, but their abundances and the rates of the interactions between them often remain unknown.
Even if we had a more complete picture of the component abundances and their reaction rates, we would still often be unable to describe how the abundances change over time because of our lack of expertise in describing the dynamics of biochemical networks. Most theoretical approaches rely on a linearization of the rate equations and assume that the components are well stirred and obey Gaussian statistics. However, in living cells, it is well known that the components are often distributed nonuniformly in space and that the interactions between them can be highly nonlinear. Such systems are notoriously difficult to treat analytically.
So, can we make firm general statements about the noise characteristics of components embedded in systems that are only sparsely determined? Hilfinger et al. now show that we can. By combining ideas and concepts from statistical physics and queuing theory (the mathematical theory of waiting lines), they derive general relationships between the average abundances, lifetimes, changes in the number of copies due to the reactions, as well as the variances and covariances, which describe how pairs of components fluctuate relative to each other. The resulting expressions make it possible to derive fundamental bounds on these quantities for certain components, even when the dynamics of the other components are unknown or unspecified.
Hilfinger et al. apply their general framework to two interesting and important problems. The first deals with protein complexes, which are well-defined assemblies of many different cellular proteins. Unbalanced production rates result in an excess of some species and a shortage of others. Cellular systems can minimize this imbalance by tuning gene expression (i.e., protein production) rates, but they can never fully eliminate it because of fluctuations in gene expression. Applying their framework to this problem, Hilfinger et al. showed that high assembly efficiency, i.e., a high average fraction of proteins that end up in the complex rather than being “wasted” through degradation, produces large fluctuations in the pool of free proteins. As an example, suppose protein A and protein B combine in a cell to give complex C. If there is a shortage in A, a highly efficient assembly process will rapidly utilize any new copies of A, thus reinforcing the shortage. This shows that while fluctuations can result from small copy-number (e.g., gene expression) fluctuations, they may also be an unavoidable byproduct of efficient processes.
In a second application, the authors prove that fluctuations may similarly be a consequence of effective control. Living cells abound with control systems—regulatory chemical networks that maintain stability in key processes or quantities, such as the osmotic pressure. While these control systems keep fluctuations in some parts of the system under control, Hilfinger et al. show that these stabilizers inevitably generate large fluctuations in other parts of the system.
So far, cellular biophysics has tried to identify and characterize the dynamics of small network motifs, the building blocks of cellular networks. The trouble is that these motifs are not isolated, but are instead embedded in larger systems that are often poorly characterized. The work of Hilfinger et al. shows that it is possible to derive general bounds on the behavior of these motifs, irrespective of how they affect and are affected by the rest of the system. These bounds yield testable predictions on what these systems can and cannot do in, for example, noise reduction, and can be used to test kinetic models against data.
More generally, the paper highlights progress being made in deriving fundamental limits on the behavior of a wide range of biological processes. For example, recent work on cellular sensing proved that the sensing precision of all equilibrium systems is fundamentally limited by the number of receptors [3]. This means that the sensing error cannot be reduced below a hard bound set by the number of receptors that bind the ligand molecules. Related efforts have found limits for cellular sensing in nonequilibrium systems [4], as well as for the fidelity of cellular “error-correction” schemes called kinetic proofreading [5–7]. The work of Hilfinger et al. provides hope that bounds like these can be generalized to any cellular biochemical network.
This research is published in Physical Review Letters.
References
- A. Hilfinger, T. M. Norman, G. Vinnicombe, and J. Paulsson, “Constraints on fluctuations in sparsely characterized biological systems,” Phys. Rev. Lett. 116, 058101 (2016).
- M. B. Elowitz, A. J. Levine, E. D. Siggia, and P. S. Swain, “Stochastic Gene Expression in a Single Cell,” Science 297, 1183 (2002).
- C. C. Govern and P. R. ten Wolde, “Energy Dissipation and Noise Correlations in Biochemical Sensing,” Phys. Rev. Lett. 113, 258102 (2014).
- C. C. Govern and P. R. ten Wolde, “Optimal Resource Allocation in Cellular Sensing Systems,” Proc. Natl. Acad. Sci. U.S.A. 111, 17486 (2014).
- J. J. Hopfield, “Kinetic Proofreading: A New Mechanism for Reducing Errors in Biosynthetic Processes Requiring High Specificity,” Proc. Natl. Acad. Sci. U.S.A. 71, 4135 (1974).
- J. Ninio, “Kinetic Amplification of Enzyme Discrimination,” Biochimie 57, 587 (1975).
- A. Murugan, D. A Huse, and S. Leibler, “Discriminatory Proofreading Regimes in Nonequilibrium Systems,” Phys. Rev. X 4, 021016 (2014).