Kondo Physics in a Quantum Channel
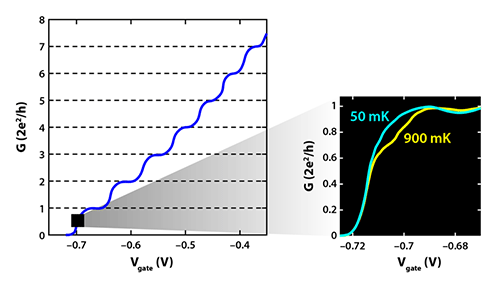
A basic building block of nanoelectronic devices is a quantum point contact (QPC), a narrow, flat channel whose width is comparable to the wavelength of an electron. Unlike a classical wire, in which the conductance varies continuously with the wire’s width, a QPC’s conductance only changes in quantized steps of 2e2∕h ( e is the electron charge, h is Planck’s constant) [1]. These steps (Fig. 1) have been observed in QPCs made from a variety of materials, and they are a hallmark of mesoscopic physics. But almost universally, they exhibit what looks like a blip: an additional small shoulder-like suppression in conductance at around (0.7)2e2∕h [2], which disappears as the QPC is cooled to absolute zero. The origin of this so-called 0.7 anomaly has been debated for twenty years [3]. Now, Hermann Sellier of the University of Grenoble Alpes, France, and colleagues provide the most direct experimental evidence to date that the anomaly is associated with the Kondo effect, a many-body interaction between itinerant electrons and localized electron spins [4]. Understanding such interactions may be relevant for the design of QPC-based devices in which spins store quantum information.
QPCs are usually created electrostatically by applying a negative voltage to two closely spaced metallic pads (gates) that rest on top of a 2D electron gas. The voltage depletes electrons immediately beneath the gates, leaving only a narrow channel of electrons—the QPC—between the gates. The 2D electron gases on either end of the QPC act as reservoirs of charge, and the width of the QPC can be controlled with the voltage on the gates.
Quantized conductance occurs only in a clean QPC, that is, one in which electrons travel a relatively long distance before scattering (ballistic transport). The size of each conductance step (2e2∕h) can be determined from a straightforward quantum-mechanical calculation of the transmission of noninteracting quantum waves across a barrier; the factor of 2 comes from the twofold degeneracy associated with electron spin. However, using this simple picture of noninteracting electrons, researchers have been unable to explain the 0.7 anomaly, which is seen in QPCs made from gallium arsenide, silicon, and graphene. This suggests the anomaly may involve electron interactions.
A clue to the origin of the 0.7 anomaly is its temperature dependence. Specifically, as a QPC is cooled, the suppression in conductance at the 0.7 shoulder goes away (Fig. 1, right). Similar behavior is observed in the conductance of electrons tunneling through quantum dots, which are nanometer-sized semiconductor islands connected to metallic leads. Because a quantum dot is small, its capacitance is small, and there is a large charging-energy cost for a single electron to tunnel onto the dot. This leads to an effect known as Coulomb blockade, in which the number of electrons on the dot is fixed and conductance through the dot is suppressed for a large range of voltages. However, when the dot possesses an odd number of electrons—a net spin—electrons in the leads collectively act to screen the spin. This Kondo interaction counteracts Coulomb blockade and enhances the conductance in the dot. Significantly, this enhancement grows with decreasing temperature, like the temperature dependence of the 0.7 shoulder in QPCs. Accordingly, researchers have connected the suppressed conductance in a QPC at the 0.7 shoulder with Coulomb blockade. Here, the idea is that when an electron is in the QPC, it reduces the probability that another electron with opposite spin can also be transmitted, so the conductance drops below 2e2∕h. A similar connection has been drawn between the disappearance of the suppression in conductance at the 0.7 shoulder in a QPC and Kondo physics in a quantum dot.
The similarities between quantum dots and QPCs were first reported in 2002 [5], and both the dependence of the conductance (near the 0.7 step) on magnetic field and the bias voltage along the QPC are consistent with Kondo physics. Despite these parallels, this explanation for the QPC anomaly is not full proof. The reason is that the Kondo interaction is normally associated with electron spins that are localized in space, like those on a quantum dot. However, the electron wave functions (and their associated spins) on a QPC are delocalized. And while theorists have suggested that quasibound (localized) electron spin states can develop in a QPC [6], there is no consensus—even after extremely careful experiments with state-of-the-art devices—that such states exist. For example, some experiments support the idea that the anomaly comes from interaction-induced changes in the 1D density of electron states in the QPC [7], instead of Kondo physics [8]. Determining whether the 0.7 anomaly is a signature of quasibound spins in the QPC requires an experiment that is sensitive to the electrons at a microscopic level.
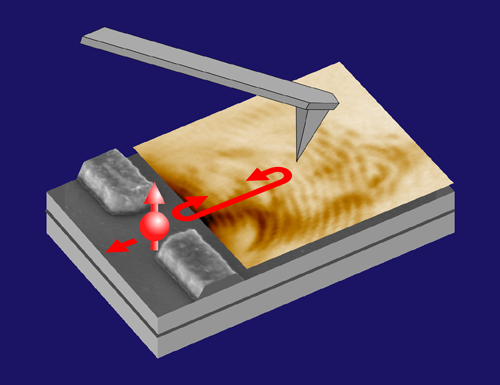
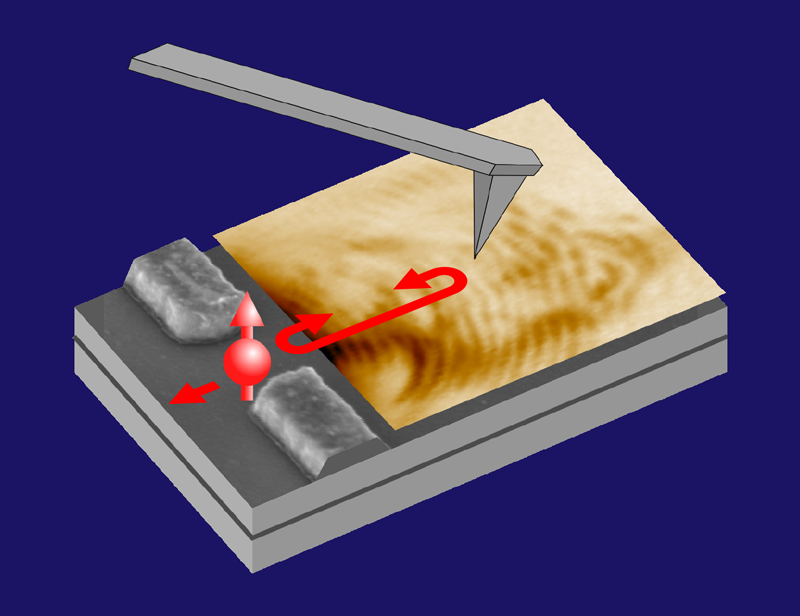
Sellier and colleagues have accessed this microscopic view by probing the electrons near a QPC with a scanning gate microscope. This tool consists of an atomically sharp tip that can both detect the electron density at a specific point in a device and apply a voltage to that point. In their experiments, the researchers placed the tip over the 2D electron gas on one side of the QPC (Fig. 2) and applied a negative voltage to the tip. This voltage depleted electrons in the region just beneath the tip, creating a local electrostatic potential (a tunnel barrier) that reflected some of the electron waves propagating out of the QPC back to the QPC, where a fraction of the waves were again reflected. In effect, the tip and the QPC acted as reflective “mirrors” for the electron waves, creating wave interference like that seen in a Fabry-Pérot interferometer.
By scanning the tip over the 2D gas outside the QPC, Sellier and colleagues could map out an interference pattern (Fig. 2). Crucially, this pattern depends on the phase change of the electron wave when it reflects from the QPC. The researchers found that this phase shift is 𝜋, and it occurs via two discrete phase jumps. Such a phase shift agrees with theoretical predictions for a Kondo interaction [9] but is in strong contrast to the continuous phase shift predicted for noninteracting electrons. The authors also confirmed that the conductance through the wire near the 0.7 step had the temperature, gate-voltage, and bias-voltage dependence expected for a Kondo interaction.
This clear proof provided by Sellier and colleagues that quasibound spins and the associated Kondo effect are the culprits of the 0.7 anomaly is relevant for many nanoelectronic devices. QPCs can, for instance, be used to convert the spin on a semiconductor quantum dot to a charge signal—a process that allows information to be read from spin-based qubits. Furthermore, researchers have recently observed features in the conductance of hybrid semiconducting-superconducting nanowire devices that are thought to be signatures of Majorana modes—quasiparticles that are their own antiparticle and are of interest for fault-tolerant quantum computing. To see these features, the nanowires have to be operated near the onset of the first conductance step at 2e2∕h, under conditions similar to those in which Sellier and colleagues have observed the Kondo effect. As such, the possibility that the conductance features in some experiments come from the Kondo interaction, and not Majorana modes, cannot be completely ruled out [10].
This research is published in Physical Review Letters.
References
- B. J. van Wees, H. van Houten, C. W. J. Beenakker, J. G. Williamson, L. P. Kouwenhoven, D. van der Marel, and C. T. Foxon, “Quantized Conductance of Point Contacts in a Two-Dimensional Electron Gas,” Phys. Rev. Lett. 60, 848 (1988); D A Wharam et al., “One-Dimensional Transport and the Quantisation of the Ballistic Resistance,” J. Phys. C 21, L209 (1988).
- K. J. Thomas, J. T. Nicholls, M. Y. Simmons, M. Pepper, D. R. Mace, and D. A. Ritchie, “Possible Spin Polarization in a One-Dimensional Electron Gas,” Phys. Rev. Lett. 77, 135 (1996).
- Adam Micolich, “Quantum Point Contacts: Double or Nothing?,” Nature Phys. 9, 530 (2013).
- B. Brun et al., “Electron Phase Shift at the Zero-Bias Anomaly of Quantum Point Contacts,” Phys. Rev. Lett. 116, 136801 (2016).
- S. M. Cronenwett, H. J. Lynch, D. Goldhaber-Gordon, L. P. Kouwenhoven, C. M. Marcus, K. Hirose, N. S. Wingreen, and V. Umansky, “Low-Temperature Fate of the 0.7 Structure in a Point Contact: A Kondo-like Correlated State in an Open System,” Phys. Rev. Lett. 88, 226805 (2002).
- T. Rejec and Y. Meir, “Magnetic Impurity Formation in Quantum Point Contacts,” Nature 442, 900 (2006).
- F. Bauer, J. Heyder, E. Schubert, D. Borowsky, D. Taubert, B. Bruognolo, D. Schuh, W. Wegscheider, J. von Delft, and S. Ludwig, “Microscopic Origin of the 0.7 Anomaly in Quantum Point Contacts,” Nature 501, 73 (2013).
- M. J. Iqbal et al., “Odd and Even Kondo Effects from Emergent Localization in Quantum Point Contacts,” Nature 501, 79 (2013).
- U. Gerland, J. von Delft, T. A. Costi, and Y. Oreg, “Transmission Phase Shift of a Quantum Dot with Kondo Correlations,” Phys. Rev. Lett. 84, 3710 (2000).
- H. O. H. Churchill, V. Fatemi, K. Grove-Rasmussen, M. T. Deng, P. Caroff, H. Q. Xu, and C. M. Marcus, “Superconductor-Nanowire Devices from Tunneling to the Multichannel Regime: Zero-Bias Oscillations and Magnetoconductance Crossover,” Phys. Rev. B 87, 241401 (2013).