Stick-Slip Motion in a Quantum Field

Mark I. Dykman

Viewpoint

Stick-Slip Motion in a Quantum Field

Department of Physics and Astronomy, Michigan State University, East Lansing, MI 48824, USA

May 16, 2016• Physics 9, 54

An electron crystal sliding on liquid helium exhibits a qualitatively new type of stick-slip motion, resulting from the coupling of the electrons to a quantum field.

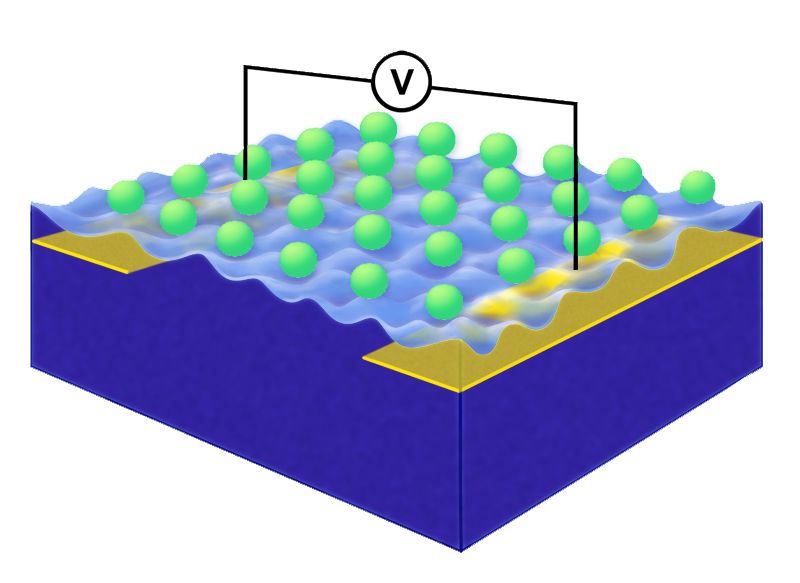
Figure caption — **Figure 1:** A Wigner crystal of electrons (green spheres) is forced to slide along the surface of liquid helium by a voltage, which is applied between two submerged metal plates (yellow strips). Rees and colleagues observed that the velocity of the crystal exhibited a type of stick-slip motion as the voltage was ramped up linearly in time.

Electrons hovering in free space a few nanometers above the surface of liquid helium constitute one of the most ideal 2D systems that scientists are able to create in the lab (Fig. 1). Because it is free from defects, this system provides a unique platform for studying many-body phenomena that are unimpeded by the disorder inherent to other condensed-matter systems. A fascinating example is Wigner crystallization [1], in which a crystalline lattice of electrons forms as a result of their purely repulsive Coulomb interaction. In fact, it was the observation of a peculiar behavior of electrons on helium that provided the first demonstration of Wigner crystallization [2, 3]. Yet in spite of its apparent simplicity, there is still much to discover about this strongly correlated system and its dynamics away from thermal equilibrium. David Rees and colleagues at RIKEN, Japan, and National Chiao Tung University, Taiwan, have now observed a qualitatively new and revealing feature of Wigner crystal dynamics [4], a stick-slip type motion of the electron lattice as it slides along the helium surface in response to a ramped up electric field.

The behavior observed by Rees and colleagues is very different in nature from the familiar stick-slip motion encountered, for example, in the friction between two solid surfaces. There, stick-slip behavior can be visualized by thinking of a particle attached to a spring that drags it over a potential landscape with multiple minima, often random in position and height [5]. If the spring’s tug is too weak, the particle will be stuck at a local minimum, but once the tug exceeds a critical value, the particle will be pulled over the potential barrier. This over-barrier transition partly releases the strain in the spring and reduces the force on the particle, which will then get stuck in another minimum until the strain again becomes sufficiently strong. This is the essence of the Prandtl-Tomlinson atomistic picture of friction, in which surface atoms provide the potential landscape. A somewhat similar picture describes the dynamics of charge- or spin-density waves coupled to random pinning centers in a solid [6].

For electrons on helium, there is no stationary potential to pin the Wigner crystal. Instead, what limits the motion of the crystal is its coupling to the quantum field of capillary waves on the helium surface; the field quanta of these waves are called ripplons. When the crystal is driven along the helium surface, electrons emit ripplons, a bit like a moving boat generates ripples on a lake. Because the electrons transfer momentum to the ripplons, there is a reaction force pushing back on the electron crystal, slowing it down. Now, if the crystal moves at a low velocity, the emitted ripplons will not interfere with each other. But the situation changes when the crystal’s velocity approaches the phase velocity $v_{0}$ of ripplons propagating in the same direction and with a wavelength equal to the interelectron spacing. Here, in a simple picture, ripplons emitted by different electrons travel in phase, and the ripplon emission rate increases sharply. This increase results from a combination of Cherenkov emission of ripplons and their Bragg diffraction, and it yields a reaction force per electron that depends on the number of electrons and diverges for an infinite crystal. Such Bragg-Cherenkov scattering [7] limits the theoretical maximum speed of the Wigner crystal to $v_{0}$ .

The saturation of the Wigner crystal velocity at $v_{0}$ was first inferred from measurements performed twenty years ago [8]. The tour de force experiment by Rees and colleagues [4] shows that a direct measurement of the crystal velocity can now be done. The researchers used an electric field to drive the electrons through a $100 - 𝜇$ m-long channel filled with helium. They then measured the resulting electron current (corresponding to the electron velocity) as a function of time. The field was produced via a voltage that was applied between two metal plates submerged in the helium and ramped up linearly in time (Fig. 1). As such, the force on the electrons resembled the tug of an increasingly stretched spring.

The researchers found that the Wigner crystal quickly reached $v_{0}$ once the electric field started to rise, moving with this velocity over the course of tens of microseconds. However, above a critical value of the field, the crystal’s velocity jumped up above $v_{0}$ by roughly an order of magnitude. The resulting charge transfer led to a drop in the field’s strength—akin to the release of the strain in a spring—and the return of the crystal’s velocity back down to $v_{0}$ . Depending on the temperature, the team observed several velocity bursts within a single ramp up of the voltage, demonstrating an analog of stick-slip behavior. To characterize this behavior, the researchers varied $v_{0}$ (by controlling the electron density) and the number of electron rows in the channel. This allowed them to determine the value of the critical electric field and its dependence on the temperature and other parameters.

The observed current outbursts represent a many-body, nonequilibrium phenomenon of a fairly general yet, so far, unexplored type. They correspond to a breaking of a barrier that is reminiscent of a high-speed object breaking the sound barrier. The key difference is that the barrier here is a consequence of strong electron correlations and the coupling of a many-electron system to a quantum field. This coupling is enhanced as the crystal velocity approaches $v_{0}$ , indicating both strong dissipation and a strong distortion of the helium surface, which is a many-electron dynamic polaronic effect [9]. The physics involved is rich and bears on many aspects of condensed-matter and statistical physics. Understanding it, however, is a formidable problem. The observations by Rees and colleagues provide an important insight into this problem and bring it into the realm of experimental accessibility.

This research is published in Physical Review Letters.

References

E. Wigner, “On the Interaction of Electrons in Metals,” Phys. Rev. 46, 1002 (1934).
C. C. Grimes and G. Adams, “Evidence for a Liquid-to-Crystal Phase Transition in a Classical, Two-Dimensional Sheet of Electrons,” Phys. Rev. Lett. 42, 795 (1979).
D. S. Fisher, B. I. Halperin, and P. M. Platzman, “Phonon-Ripplon Coupling and the Two-Dimensional Electron Solid on a Liquid-Helium Surface,” Phys. Rev. Lett. 42, 798 (1979).
D. G. Rees, N. R. Beysengulov, J. -J. Lin, and K. Kono, “Stick-Slip Motion of the Wigner Solid on Liquid Helium,” Phys. Rev. Lett. 116, 206801 (2016).
A. Vanossi, N. Manini, M. Urbakh, S. Zapperi, and E. Tosatti, “Colloquium : Modeling friction: From Nanoscale to Mesoscale,” Rev. Mod. Phys. 85, 529 (2013).
P. Monceau, “Electronic Crystals: An Experimental Overview,” Adv. Phys. 61, 325 (2012).
M. I. Dykman and Y. G. Rubo, “Bragg-Cherenkov Scattering and Nonlinear Conductivity of a Two-Dimensional Wigner Crystal,” Phys. Rev. Lett. 78, 4813 (1997).
A. Kristensen, K. Djerfi, P. Fozooni, M. J. Lea, P. J. Richardson, A. Santrich-Badal, A. Blackburn, and R. W. van der Heijden, “Hall-Velocity Limited Magnetoconductivity in a Classical Two-Dimensional Wigner Crystal,” Phys. Rev. Lett. 77, 1350 (1996).
W. F. Vinen, “Non-Linear Electrical Conductivity and Sliding in a Two-Dimensional Electron Crystal on Liquid Helium,” J. Phys. Condens. Matter 11, 9709 (1999).

About the Author

Mark Dykman is a professor of physics at Michigan State University. He has worked on various topics, including effects resulting from the interplay of decoherence, nonlinearity, and fluctuations in mesoscopic vibrational systems; Floquet dynamics of dissipative systems; transport in correlated electron systems; nonlinear optics of solids; rare events in far-from-thermal-equilibrium systems; and many-body aspects of quantum information. He is a Fellow of the American Physical Society. In 2013 he was recognized as an Outstanding Referee by the American Physical Society.