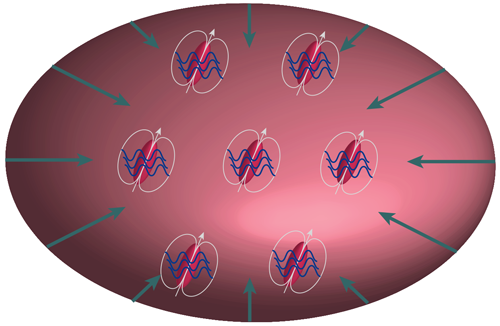
An Arrested Implosion
Macroscopic implosions of quantum matter waves have now been halted by quantum fluctuations. The quantum wave in question is an atomic Bose-Einstein condensate (BEC), a quantum state with thousands to tens of millions of atoms in an ultracold gas all sharing the same macroscopic wave function. Attractive atomic interactions can cause BECs to collapse in spectacular ways, in what’s been termed a “bosenova,” a lighthearted allusion to a supernova explosion [1]. Tilman Pfau and colleagues from the University of Stuttgart, Germany, have shown that for BECs made of dysprosium, whose bosonic isotopes are among the most magnetic atoms in the periodic table, long-range dipole-dipole interactions between these neutral atoms create a totally new phenomenon: the arrested collapse of a quantum magnetic fluid, called a quantum ferrofluid [2, 3]. Such a ferrofluid relies crucially on the strong dipolar interactions in the dysprosium gas. This attractive dipolar interaction can be nearly balanced by the repulsive, short-range van der Waals “contact” interaction, halting the implosion and allowing quantum fluctuations to stabilize a new quantum state. Quantum droplets arise, each containing hundreds of atoms in a superfluid state. Dipolar interactions among the droplets induce a lattice-like ordering into the system, creating a mesoscopic superfluid crystal (Fig. 1).
Many BEC experiments have been accurately described by a relatively simple semiclassical theory called mean-field theory [4]. For BECs, this theory takes the form of a nonlinear Schrödinger equation in which the nonlinear term is proportional to the atomic contact interaction times the local atomic density. Nonlinear Schrödinger equations describe a variety of nonlinear dynamics in BECs as well as many other physical systems. The nonlinearity comes from the density, which is given by the absolute value of the BEC wave function squared. Mean-field theory replaces the complicated quantum many-body wave function supported by an exponentially large Hilbert space with a simple semiclassical complex scalar wave function—the mean field. It also discards quantum fluctuations, correlations, and entanglement of the particles’ motional and spin degrees of freedom. Nevertheless, this simplified nonlinear equation leads to accurate descriptions of beautiful nonlinear quantum dynamics in BECs, from localized persistent structures like solitons, to crystalline lattices of vortices, to quantum turbulence. But how quantum is all this? If neither quantum fluctuations nor quantum entanglement—hallmarks of quantum many-body physics—play a significant role, and we can use a simple semiclassical mean-field description with high accuracy, can we really say a BEC is fully quantum? Just like the coherent light produced by a laser well above the lasing threshold, most properties of a BEC—a coherent matter wave—don’t require a fully quantum description, as long as the atoms are weakly interacting. While strong contact interactions can lead to the need for a more quantum description, such BECs become unstable to molecular formation, obviating our ability to make careful studies. So if one wanted to study the role of quantum fluctuations in the organization of ultracold gaseous matter, how could one coax a BEC to “step” beyond mean-field theory?
One typical way is to place the BEC in a periodic arrangement of light called an optical lattice [5], forcing a lattice structure on the gas. Remarkably, the Stuttgart group has discovered a way to produce a spontaneous lattice structure in the standard harmonic trap without the use of an optical lattice [2, 3]. They have created a system in which two effects describable by mean-field theory balance each other out, producing a golden opportunity for quantum fluctuations to step into the act. By Bose-condensing dysprosium [6], an atom with a whopping magnetic moment of 10 Bohr magnetons, and using a mechanism known as a Feshbach resonance, which can weaken the atomic contact interaction, the researchers have created a situation in which the contact interaction cancels out the attractive dipolar interaction at the level of mean-field theory, leaving the beyond-mean-field quantum fluctuations to play a considerable part.
Feshbach resonances, which can tune contact interactions over many orders of magnitude, appear when an external magnetic field induces a highly excited, bound diatomic molecular state, in this case, of , to come into resonance with scattered atoms via the Zeeman effect. Such resonances have been key to the versatility of BEC-based quantum simulators and their ability to explore a wide variety of quantum phenomena, presenting a delightful playground in which to study quantum many-body physics. In the present experiments, the resulting Feshbach-tuned BEC, rather than imploding, as mean-field theory would predict for a quantum ferrofluid, spontaneously formed a small crystalline structure of several BEC droplets. By opening the 3D harmonic trap, which confines the BEC, along one axis, the Stuttgart group coaxed these droplets into trains of miniature BECs that appear as robust elongated quantum droplets whose velocity is a measure of the interdroplet binding energy. The team could even allow these droplets to expand into each other. The resulting interference fringes in the atomic density are characteristic of mutual phase coherence among the droplets’ wave functions, just like fringes between interfering light sources are a signature of mutual phase coherence. This implies that the quantum fluctuations aren’t sufficiently strong to qualitatively disturb the BEC’s phase order. The mesoscopic coherent crystal is reminiscent of the superfluid lattices generated by optically driven BECs confined in optical resonators [7]. But unlike these coherent, checkerboard density waves, which arise from a broken discrete spatial symmetry, the broken symmetry here is continuous, presenting the possibility that phonon-like excitations may be observed in this nascent supersolid.
How can we understand this exquisite quantum experiment? First, Falk Wächtler and Luis Santos from Leibniz University of Hanover, Germany, have demonstrated quite convincingly that a modified nonlinear dipolar Schrödinger equation reproduces the experimental data [8]. This new equation adds an extra term to the standard nonlinear dipolar Schrödinger equation that factors in the quantum fluctuations the atoms feel as an effective potential. Without this extra term, the theory cannot explain the formation of self-organized crystals; it predicts an unstable gas instead. In fact, models building on mean fields and incorporating both quantum and thermal fluctuations are also at the heart of microemulsion phases discussed in the context of the 2D electron gases one finds, for example, in clean silicon MOSFET transistors. Such phases are intermediate between a Fermi liquid and a Wigner crystal of interacting electrons, and they include both quantum bubble phases akin to the droplets observed by the Stuttgart group and quantum stripe phases similar to those observed in unconventional superconductors [9].
Can we find this rich set of phases in BECs or other even more strongly dipolar systems, such as Rydberg gases, for which droplet crystals are also predicted [10]? What might happen as we turn up the interactions via a Feshbach resonance to move beyond the extant theoretical approaches that rely on perturbative treatments of interactions? Would we observe melting of the droplet crystal driven by stronger quantum fluctuations? Could exotic quantum dynamics be observed after an interaction quench? If so, we might learn much about how quantum matter organizes to form new phases and whether or not our theories of quantum many-body physics provide a correct description in untested macroscopic and strongly interacting regimes. On the theory side, we can address such questions by taking advantage of the wealth of powerful finite-temperature quantum-fluctuation-based numerical methods that have appeared over the last two decades [11]. The Stuttgart group has opened our eyes to a whole new world of quantum possibility.
This research is published in Physical Review Letters and Nature.
References
- E. A. Donley, N. R. Claussen, S. L. Cornish, J. L. Roberts, E. A. Cornell, and C. E. Wieman, “Dynamics of Collapsing and Exploding Bose–Einstein Condensates,” Nature 412, 295 (2001); J. Thompson, “Researchers Have the Bosenova Blues,” Nature News (2001).
- I. Ferrier-Barbut, H. Kadau, M. Schmitt, M. Wenzel, and T. Pfau, “Observation of Quantum Droplets in a Strongly Dipolar Bose Gas,” Phys. Rev. Lett. 116, 215301 (2016).
- H. Kadau, M. Schmitt, M. Wenzel, C. Wink, T. Maier, I. Ferrier-Barbut, and T. Pfau, “Observing the Rosensweig instability of a quantum ferrofluid,” Nature 530, 194 (2016).
- Emergent Nonlinear Phenomena in Bose-Einstein Condensates: Theory and Experiment, edited by P. G. Kevrekidis, D. J. Frantzeskakis, and R. Carretero-Gonzalez (Springer, Berlin, 2008)[Amazon][WorldCat].
- I. Bloch, J. Dalibard, and W. Zwerger, “Many-Body Physics with Ultracold Gases,” Rev. Mod. Phys. 80, 885 (2008).
- M. Lu, N. Q. Burdick, S. Ho Youn, and B. L. Lev, “Strongly Dipolar Bose-Einstein Condensate of Dysprosium,” Phys. Rev. Lett. 107, 190401 (2011).
- R. Landig, L. Hruby, N. Dogra, M. Landini, R. Mottl, T. Donner, and T. Esslinger, “Quantum Phases from Competing Short- and Long-Range Interactions in an Optical Lattice,” Nature 532, 476 (2016).
- F. Wächtler and L. Santos, “Quantum Filaments In Dipolar Bose-Einstein Condensates,” arXiv:1601.04501.
- B. Spivak and S. A. Kivelson, “Phases Intermediate Between a Two-Dimensional Electron Liquid and Wigner Crystal,” Phys. Rev. B 70, 155114 (2004).
- F. Cinti, P. Jain, M. Boninsegni, A. Micheli, P. Zoller, and G. Pupillo, “Supersolid Droplet Crystal in a Dipole-Blockaded Gas,” Phys. Rev. Lett. 105, 135301 (2010).
- Quantum Gases: Finite Temperature And Non-Equilibrium Dynamics, Vol. 1, edited by N. P Proukakis, S. A Gardiner, M. Davis, and M. Szymanska (Imperial College Press, 2013)[Amazon][WorldCat].