A glassy counterpart to supersolids

Zohar Nussinov

Viewpoint

A glassy counterpart to supersolids

Department of Physics, Washington University, St. Louis, MO 63160, USA

December 8, 2008• Physics 1, 40

A new phase of matter called a superglass may be possible, as shown by an investigation of the quantum mechanical analog of a classical hard sphere glass.

Figure caption — **Figure 1:** (a) A classical system of Brownian spheres may crystallize at low temperatures if cooled slowly. By contrast, a bi-disperse system (i.e., consisting of two different kinds of hard spheres) such as the one shown cannot crystallize and will jam into a glass at high densities and low temperatures. Similarly, a rapidly cooled system of hard spheres does not have enough “time” to crystallize and forms a glass instead. Using the mapping of [7], it is seen that the quantum analog of the classical hard-sphere Brownian system is that of spheres with sticky interactions. In the classical hard-sphere limit, only pair interactions appear in the corresponding quantum system. (b) The pair potential in the corresponding quantum system given by Biroli *et al.* [1] (for two values of $λ$ , a parameter that adjusts how hard the classical potential is, where $r$ is the interparticle distance and $σ$ is the sphere diameter) and the corresponding phase diagrams, shown in (c). Top: The solid curve indicates the classical Brownian hard-sphere phase diagram (pressure $P$ versus volume fraction $ϕ$ ) for uniform annealed systems wherein spheres forming a liquid at low densities pack into a face-centered-cubic (FCC) crystal structure at high densities. The dashed curve shows the phase diagram of a rapidly quenched or bi-disperse system in which crystallization is thwarted and the system becomes a glass instead [random close packing (RCP)]. Bottom: The corresponding quantum phases obtained by the map of [7]. The liquid-to-solid transition of the classical Brownian sphere system maps into a superfluid to supersolid transition. Similarly, the superfluid to superglass transition constitutes an analog of the classical liquid to glass transition. [ Panels (b) and (c) adapted from Biroli *et al.* [1].]

Glasses are liquids that have ceased to flow on experimentally measurable time scales. By constrast, superfluids flow without any resistance. The existence of a phase characterized by simultaneous glassiness and superfluidity may seem like a clear contradiction. However, in a paper in Physical Review B, Giulio Biroli (Institut de Physique Théorique, France), Claudio Chamon (Boston University), and Francesco Zamponi (École Normale Supérieure, France) prove that this is not so [1] and illustrate theoretically the possibility of a “superglass” phase. This phase forms an intriguing amorphous counterpart to the “supersolid” phase [2,3] that has seen a surge of interest in recent years [4]. Within a “supersolid” phase, superfluidity can occur without disrupting crystalline order.

Interacting quantum particles can indeed form such a superglass phase at very low temperatures and high density, and the work of Biroli et al. confirms the earlier suggestion by Boninsegni, Prokof ’ev, and Svistunov [5] and an investigation by Wu and Philips [6] of such a phase. The superglass phase is characterized by an amorphous density profile, yet at the same time a finite fraction of the particles flow without any resistance as if they were superfluid. Thus the superglass constitutes a glassy counterpart to the supersolid phase.

The approach invoked by Biroli et al. to prove the existence of a superglass is particularly elegant. It relies on mapping [7] viscous classical systems, whose properties are well known, to new many-body quantum systems. In realizing the link between classical and quantum systems to gain insight into the quantum many-body phases, Biroli et al. nicely add an important new result to earlier investigations that built on such similar insights elsewhere. Chester [3] suggested the existence of a supersolid by relying on such a connection. In a similar fashion, Laughlin invoked a highly inspirational analogy [8] between variational (the so-called Jastrow type) wave functions describing fractional quantum Hall systems and a previously studied system of classical charged particles interacting via a logarithmic potential. By using the classical plasma analogy and using known results on it, Laughlin was able to make headway on the challenging many-body quantum problem and construct his highly successful wave functions.

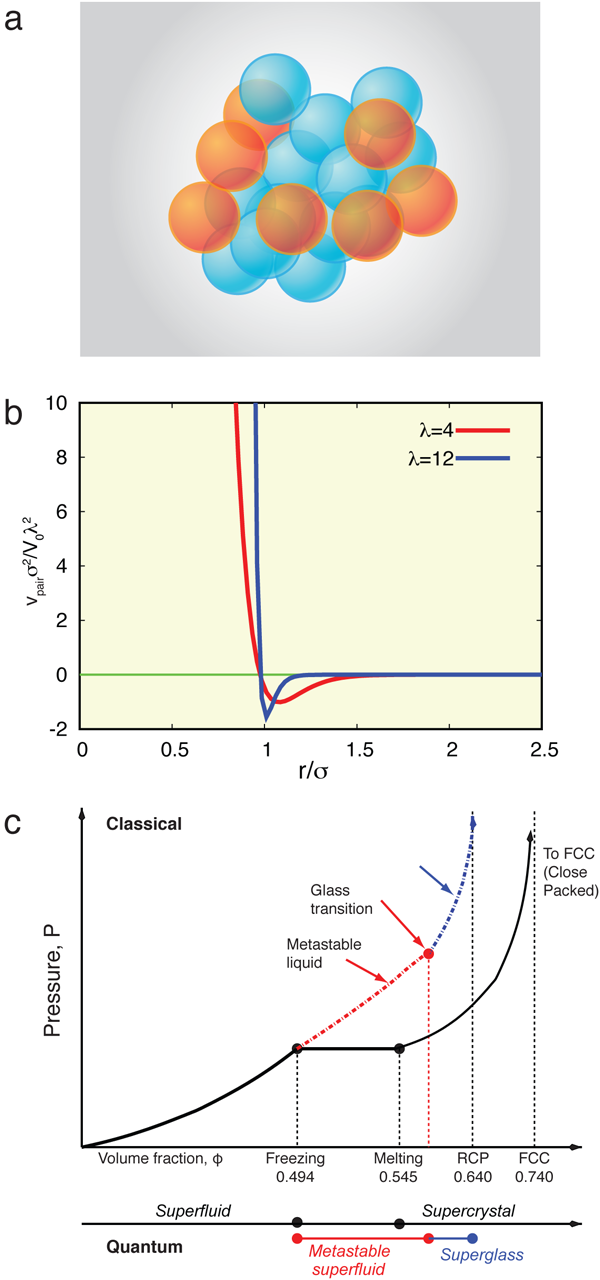
The mapping used by Biroli et al. similarly enables exact results on the quantum problem of superglasses and a detailed correspondence of spatial and temporal correlations between the classical and quantum systems. The authors apply this mapping to a classical system well known to exhibit glassy dynamics—the Brownian hard sphere problem. The quantum counterpart of the classical hard sphere problem is a natural system containing hard sphere interactions [Fig. 1(a),1(b)]. On the classical side of the correspondence, the hard sphere system has been heavily investigated [9–11]. When the sphere packing density is slowly varied, the classical Brownian hard sphere system undergoes a transition from a liquid at low density to an ordered crystal at high density [9]. When crystallization is thwarted by a rapid increase of the packing density or by, for example, a change of the particle geometry, the system cannot order nicely into a crystal and instead jams into a dense amorphous glass [10,11].

Biroli et al. noticed that by using the mapping between quantum systems with classical glass-forming systems such as the Brownian spheres, they can obtain nontrivial results. In its simplest form, the mapping of [7] casts the first-order differential equation in time for the dynamics of viscous classical particles as a Schrödinger equation with an effective Hamiltonian. Biroli et al. find that under this mapping, the glassy phase of the classical system translates into a quantum glass of a Bose system. Similarly, the classical solid maps onto a quantum bosonic crystal, resulting in an interesting phase diagram [Fig.1(c)]. The spatiotemporal correlations of the (bosonic) quantum counterpart may be computed by mapping to the classical system. Both the glassy and solid phases harbor a finite Bose-Einstein condensate fraction. Putting all of the pieces together, Biroli et al. provide an important proof of concept of the superglass phase in a simple and precise way. This route may be replicated for classical systems other than the Brownian hard sphere that also display solid and glass phases.

What physical systems might exhibit the new superglass phase? Recent experiments [4,12] on solid helium-4 exhibit supersolid-type features and have led to a flurry of activity. In the simplest explanation of observations, a fraction of the medium becomes, at low temperatures, a superfluid that decouples from the measurement apparatus. However, the condensate fraction that is required for such an explanation to account for the data does not simply conform with thermodynamic measurement [12]. Rittner and Reppy [13] further found that the measured putative supersolid-type feature is acutely sensitive to the quench rate for solidifying the liquid, while Aoki, Keiderling, and Kojima observed rich hysteresis and memory effects [14]. All of these features can arise from glassy characteristics alone [15,16]—precisely as in the superglass phase discussed by Biroli et al. It may be that a confluence of both superfluid and glassy features (and their effects on elastic properties of a medium) [17] is at work.

These effects should be observable as experimental consequences of (super-) glassy dynamics, such as disparate relaxation times that could be measured [15]. Typical glass formers indeed typically exhibit relaxations on two different time scales. Cold atom systems may provide another realization of a superglass state. Indeed, a supersolid state of cold atoms in a confining optical lattice was very recently achieved [18]. It is natural to expect a superglass analog of these cold atomic systems.

Superglasses may also have realizations in other areas such as superconductivity and I speculate on these below. For example, consider a lattice version of the continuum system investigated by Biroli et al.: a “lattice superglass.” For charged bosons (e.g., Cooper pairs) on a lattice, such a superglass would correspond to a superconductor with glassy dynamics. In a similar vein, a “lattice supersolid” of Cooper pairs would correspond to a superconductor concomitant with well-defined crystalline (i.e., charge-density wave) order. Indeed, in some heavy fermion compounds as well as in the cuprate and the newly discovered iron arsenide family of high-temperature superconductors [19] there are some indications of nonuniform mesoscale spatial electronic structures and glassy dynamics. Classical glass formers are known to exhibit “dynamical heterogeneities”—a nonuniform distribution of local velocities [20]. I also speculate that “quantum dynamical heterogeneities” may be derived by applying the mapping used by Biroli et al. to classical glass forming systems that exhibit dynamical heterogeneities..

“Spin superglasses” are another possibility. Quantum spin systems in a magnetic field [21] can exhibit a delicate interplay between the formation of singlet states and the tendency of spins to align with the field direction. These systems can be mapped onto a system of bosons with hard-core interactions—just as in the system investigated by Biroli et al. In some spin $S = 1 / 2$ antiferromagnets in an external magnetic field, triplet states with spins aligned along the field direction can be regarded as hard-core bosons. In many other systems, interactions between quantum spins may also be mapped onto hard-core-type bosonic systems [22,23]. Invoking these bosonic representations, if a solid or glassy phase appears in a classical Brownian system, then a mapping similar to that of Biroli et al. suggests supersolidity/superglassiness in the corresponding quantum spin system. Recently, there has been much work examining supersolidity in such spin systems, e.g., [23]. It is highly natural to expect new lattice spin superglass counterparts

Finally, even more intriguing superglasses might be possible. In transition-metal compounds, the fractional filling of the $3 d$ atomic shells allows for cooperative orbital ordering [24]. Perhaps low-temperature Bose-condensed glasses of orbitals could appear, forming an orbital superglass. The orbital states may be described by pseudospins [24] that may be mapped to hard-core bosons [22]. The work of Biroli et al. allows us to investigate the possibility of an orbital superglass by knowing the dynamics of hard-core Bose model derived from a classical counterpart. In addition, the classical-to-quantum map of [7] may also suggest a new quantum critical point in related systems. The classical zero temperature jamming transition [25] of hard spheres or disks is a continuous transition with known (dynamical) critical exponents, e.g., [26,27]. Replicating the mapping used by Biroli et al., we may derive an analog quantum system harboring a zero temperature transition with similar critical exponents. Thus the classical critical point [25–27] may rear its head anew in the form of “quantum critical jamming.” All of the systems discussed above were free of quenched disorder. Applying the same mapping to classical viscous systems with quenched disorder, we may further arrive at quenched super spin glass analogs of classical spin glass systems [28]. The tantalizing superglass phase may have numerous ramifications.

References

G. Biroli, C. Chamon, and F. Zamponi, Phys. Rev. B 78, 224306 (2008)
A. F. Andreev and I. M. Lifshitz, Sov. Phys. JETP 29, 1107 (1969); G. V. Chester and L. Reatto, Phys. Rev. 155, 88 (1967); L. Reatto, 183, 334 (1969); A. J. Leggett, Phys. Rev. Lett. 25, 1543 (1970); P.W. Anderson, Basic Notions of Condensed Matter Physics (Benjamin, Menlo Park, CA, 1984)
G.V. Chester, Phys. Rev. A 2, 256 (1970)
E. Kim and M. H. Chan, Science 305, 1941 (2004); E. Kim and M. H. W. Chan, Nature 427, 225 (2004)
M. Boninsegni, N. Prokof ’ev, and B. Svistunov, Phys. Rev. Lett. 96, 105301 (2006)
J. Wu and P. Phillips, Phys. Rev. B 78, 014515 (2008)
G. Parisi, Statistical Field Theory (Addison Wesley, New York, 1988); J. Zinn-Justin, Quantum Field Theory and Critical Phenomena (Oxford University Press, 2002)
R. B. Laughlin, Phys. Rev. Lett. 50, 1395 (1983)
W. G. Hoover and F. H. Ree, J. Chem. Phys. 49, 3609 (1968)
T. R. Kirkpatrick and P. G. Wolynes, Phys. Rev. A 35, 3072 (1987)
W. van Megen and S. M. Underwood, Phys. Rev. Lett.70, 2766 (1992)
http://physics.aps.org/articles/v1/16
A. S. C. Rittner and J. D. Reppy, Phys. Rev. Lett. 98, 175302 (2007)
Y. Aoki M. C. Keiderling and H. Kojima, Phys. Rev. Lett. 100, 215303 (2008)
A. V. Balatsky, Z. Nussinov, M. J. Graf, and S. A. Trugman, Phys. Rev. B 75, 094201 (2007); Z. Nussinov, A. V. Balatsky, M. J. Graf, and S. A. Trugman, 76, 014530 (2007); M. J. Graf, Z. Nussinov, and A. V. Balatsky (to be published)
C-D. Yoo and A. Dorsey, arXiv: 0810.2525 (2008)
J. Zannen, Z. Nussinov, and S. I. Mukhin, Ann. Phys. 310, 181 (2004); V. Cvetkovic and J. Zaanen, Phys. Rev. Lett. 97, 045701 (2006); V. Cvetkovic, Z. Nussinov, S. Mukhin, and J. Zaanen, Europhys. Lett. 81, 27001 (2008)
A. Koga, T. Higashiyama, K. Inaba, S. Suga, and N. Kawakami, J. Phys. Soc. Jpn 77, 073602 (2008)
Yi Yin, M. Zech, T. L. Williams, X. F. Wang, G. Wu, X. H. Chen, and J. E. Hoffman, arXiv:0810.1048 (2008)
H. Sillescu, J. Non-Cryst. Solids 243, 81 (1999); M.D. Ediger, Ann. Rev. Phys. Chem. 51, 99 (2000); R. Richert, J. Phys. Condens. Matter 14, R703 (2002); W. Kob, C. Donati, S.J. Plimpton, P.H. Poole, and S.C. Glotzer, Phys. Rev. Lett. 79, 2827 (1997); C. Donati, J.F. Douglas, W. Kob, S.J. Plimpton, P.H. Poole, and S.C. Glotzer, 80, 2338 (1998); S.C. Glotzer, J. Non-Cryst. Solids 274, 342 (2000); Y. Gebremichael, T.B. Schroder, F.W. Starr, and S.C. Glotzer, Phys. Rev. E 64, 051503 (2001)
K. Kodma, et al., Science 298, 395 (2002)
T. Matsubara and H. Matsuda, Prog. Theor. Phys. 16, 569 (1956)
P. Sengupta and C. D. Batista, Phys. Rev. Lett. 98, 227201 (2007)
J. van den Brink, G. Khaliullin, and D. Khomskii in Colossal Magnetoresistive Manganites, edited by T. Chatterij (Kluwer Academic Publishers, Dordrecht, 2002); arXhiv:cond-mat/0206053, and references therein
A.J. Liu and S.R. Nagel, Nature 396 21 (1998)
J. A. Drocco, M. B. Hastings, C. J. Olson Reichhardt, and C. Reichhardt, Phys. Rev. Lett. 95, 088001 (2005)
T. Hatano, arXiv:0807.3678 (2008)
M. Mezard, G. Parisi, and M. A. Virasoro, Spin Glass Theory and Beyond (World Scientific, Singapore, 1987)

About the Author

Zohar Nussinov received his B.Sc. from Tel-Aviv University and his Ph.D. from UCLA (2000). Since 2005, he has been an assistant professor in the physics department at Washington University, St. Louis.