Pushing the envelope of general relativity
Einstein introduced general relativity in the early 20th century, and since then it has been proven to be an accurate description of gravity beyond the regime of validity of Newtonian gravitation. Since then, people have been asking what kind of modifications, or extensions, one can make to it without contradicting observations. In most cases, the focus has been on theories that respect the physical principles of general relativity, and the modifications were restricted to the action (an appropriate quantity integrated over a path in spacetime between a starting point and ending point) and the equations of motion that the action encodes, via the principle of least action. In particular, if quantum mechanics describes gravitation as well as the other forces of nature, as is widely believed, quantum corrections should introduce small modifications to the action. However, the study of possible corrections that disobey the physical principles of general relativity has recently received a boost by the theory recently proposed by Hořava [1,2], which posits the violation of a key symmetry principle thought to be sacrosanct—Lorentz invariance—at short distance scales. Now, in a paper in Physical Review Letters, Hong Lu, Jianwei Mei, and Christopher Pope of Texas A&M University, US, report their investigations [3] into how the modifications proposed in Hořava’s theory affect generic solutions of general relativity.
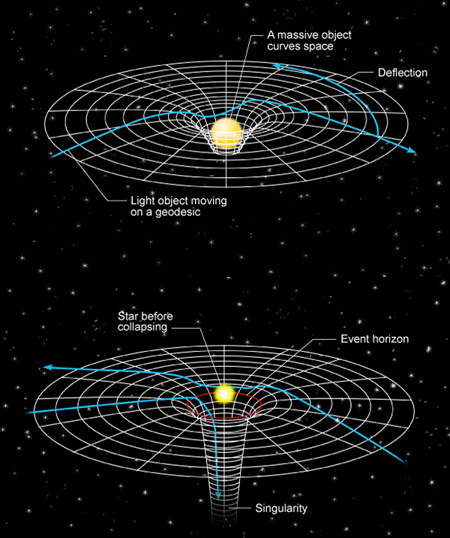
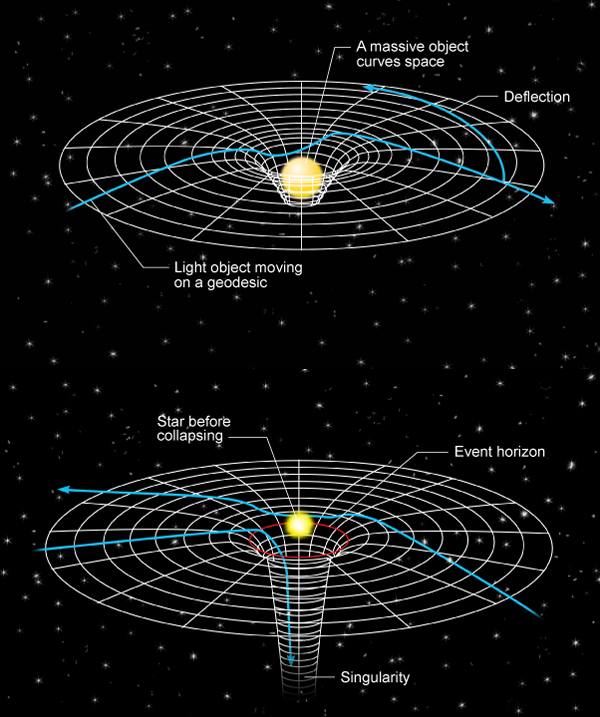
General relativity is a beautiful theory, whose main physical insight is that gravity is the effect of geometry, specifically, the curvature of spacetime. Matter curves spacetime, and in turn, the curvature of spacetime deflects massive bodies, which we then interpret as the influence of gravity (Fig. 1). A natural consequence appears to be the principle of general covariance (which is what is meant by “general” relativity), namely, that physics should be the same in all reference frames, not merely inertial ones. That is, under a general coordinate transformation xμ→x′μ ( xν), where the four-vector xμ=(t,x), the physics should be invariant. However, no physical principle dictates the exact form of the action, beyond general coordinate invariance. For action, Einstein used the integral of R (the scalar measure of the curvature at each point), because it reproduces Newtonian gravity in the appropriate limit (small curvature R, small velocity). But one can certainly add small covariant corrections, such as a power of the curvature scalar. In fact, such terms do appear as quantum corrections in the only known quantum theory that includes gravity, namely, string theory. In that case, however, general covariance remains satisfied.
The experimental tests of general relativity are very stringent. Perhaps the most impressive everyday application is the satellite global positioning system, whose deviations in the absence of general relativity corrections would add up to about 10km per day [4]. But today we have many more constraints from astrophysics, and we know general relativity is correct to a large degree of accuracy. Perhaps more importantly, if corrections to the Einstein action break general covariance, we have to have a good theoretical justification, since generally when we break an important symmetry, quantum corrections spell disaster for the theory, amplifying the problem.
There is, however, an example that served as a model for Hořava’s theory. The example, due to Lifshitz [5], involves the appearance of Lorentz symmetry (which says, in the absence of gravity, that physics is the same for all inertial observers moving through space) as an accidental symmetry at large distances in a simple scalar theory without Lorentz invariance. Lifshitz’s theory has the usual Galilean invariance of Newtonian mechanics. Quantum corrections, which become larger at larger distances, were shown to give rise to a Lorentz invariant theory at distances much larger than the scale at which the theory is defined. In his original work, Lifshitz was discussing the behavior of critical points (such as the triple point) in condensed matter systems.
In Hořava’s theory, we have the same idea applied to gravity. The theory, defined at small distances, has the natural generalization of Galilean invariance, namely, general covariance in the space coordinates, x→x′(x) and invariance under time reparametrizations, t→t′(t). Again, quantum corrections are expected to give rise to a general coordinate invariant theory at large distances. The arguments for this are not so strong as in the case of the Lifshitz theory, since the quantization of gravity, even in the Hořava version, is not very well defined. What makes the Hořava theory so compelling, however, is the fact that the most naive attempt at quantization seems not to produce the same nonsensical infinite results one gets in general relativity. Therefore what was a physical principle for Einstein appears as an accidental symmetry in Hořava’s theory, but the upside is that it is much easier to introduce quantum mechanics.
Assuming that quantum corrections work as expected in Hořava’s theory, it will give the proper action for general relativity at large distances, and correction terms that start to dominate at short distances, and break general covariance. A priori there is a very large number of such possible terms, but Hořava proposed also a simplified version, the “detailed balance action.” (The name is given by analogy, it has no meaning in gravity. A formal similarity with equations appearing in the quantum description of some thermodynamical systems prompted the name.)
In the work of Lu et al. [3], a general spherically symmetric solution to Hořava’s detailed balance action is investigated. In general relativity, the most general spherically symmetric solution is the Schwarzschild solution, describing everything from planets like the earth to black holes. However, the solution of the detailed balance action of Hořava deviates significantly from the Schwarzschild solution, a reflection of the difficulty of modifying general relativity. A small modification of the detailed balance action has a solution closer to the Schwarzschild solution.
Based in part on the results of Lu et al., I found [6] that if we were to apply the detailed balance action to the real world, general relativity would be reproduced only on unobservable scales, larger than the size of the Universe (the “cosmological horizon”). Modifications of the detailed balance action, within Hořava theory, can cure this problem. For instance, one natural modification was proposed in [6], and another in [7]. It is still not known if the quantum Hořava theory makes sense, and more work in that direction is needed.
Finally, we should mention that other small modifications of general relativity were proposed over the years, and whether any of them makes sense is still an open problem. Some of the better-known examples are the Dvali-Gabadadze-Porrati model [8], which modifies general relativity at very large distances, and the purely phenomenological Modified Newtonian Dynamics (MOND) [9], which modifies Newtonian gravity at small accelerations and large scales. However, unlike these other cases, Hořava theory presents the tantalizing possibility that we have a well-defined quantum theory at short distances, without the need for additional fields.
The only known way to have a well-defined quantum theory at short distances that preserves general covariance—string theory—needs to postulate an infinite number of kinds of particles, the excitations of the string, all of them interacting with gravity. If a version of Hořava theory is correct, would that circumvent the need for string theory? Not necessarily, since we still would need a consistent quantum theory of all kinds of particles in nature, interacting with gravity, and it is difficult to see how Hořava theory would accommodate that by itself. It is conceivable that pure Hořava gravity theory could arise as a limit of string theory, just as, say, pure electromagnetism arises as a limit of string theory, but only time and a lot more work will tell us.
References
- P. Hořava, Phys. Rev. D 79, 084008 (2009); Phys. Rev. Lett. 102, 161301 (2009)
- P. Hořava, JHEP 03, 020 (2009)
- H. Lü, J. Mei, and C. N. Pope, Phys. Rev. Lett. 103, 091301 (2009)
- See, e.g., and Neil Ashby, Physics Today 55, 41 (2002)
- E. M. Lifshitz, Zh. Exp. Theor. Phys. 11, 255 (1941); 11, 269 (1941)
- H. Nastase, arXiv:0904.3604
- A. Kehagias and K. Sfetsos, Phys. Lett. B 678, 123 (2009)
- G. R. Dvali, G. Gabadadze, and M. Porrati, Phys. Lett. B 485, 208 (2000)
- M. Milgrom, Astrophys. J. 270, 365 (1983); 270, 371 (1983); 270, 384 (1983)