Does quantum mechanics play a role in critical phenomena?

Rajiv R. P. Singh

Viewpoint

Does quantum mechanics play a role in critical phenomena?

Department of Physics, University of California, Davis, CA 95616, USA

April 26, 2010• Physics 3, 35

Quantum interference effects can, in theory, lead to the emergence of new particles carrying exotic quantum numbers at a critical point. But how good is the evidence that this happens?

Figure caption — **Figure 1:** Schematic phase diagram with two very different spin configurations. At the deconfined quantum critical point $g_{c}$ , the Néel order parameter $O_{1}$ and the valence bond crystal order parameter $O_{2}$ vanish continuously from the two sides and spin- $1 / 2$ excitations (shown in inset as a free spin in a sea of singlet pairs) become deconfined. At this point, free spinons and photons emerge as dynamical variables in the system.

Critical phenomena are associated with the cooperative fluctuations of a large number of microscopic degrees of freedom [1]. At the well-known liquid-gas critical point, quantum mechanics is largely irrelevant. However, when the critical point is pushed down to $T = 0$ , as in the case of a uniaxial magnet in a transverse field [2], the divergent length scale is the result of quantum rather than thermal fluctuations. Quantum systems with fluctuating spacetime field configurations map onto field theories in one extra dimension [3]. In analogy with phenomena like the Aharonov-Bohm effect, where spatial trajectories that return to the starting point acquire a quantum mechanical phase, these field theories have complex Berry phases that arise from overlap between quantum states at nearby times [3] and so are not like classical statistical systems. If one ignores Berry phases, as is possible in some models, then one obtains classical behavior. But in many cases these Berry phases cannot be ignored [4]. And, indeed, the widespread observation of exotic phases in strongly correlated materials, such as heavy fermions [5] and cuprates [6], right near the quantum critical point, suggests a greater richness of quantum critical phenomena.

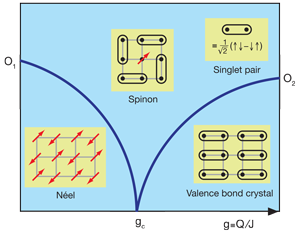
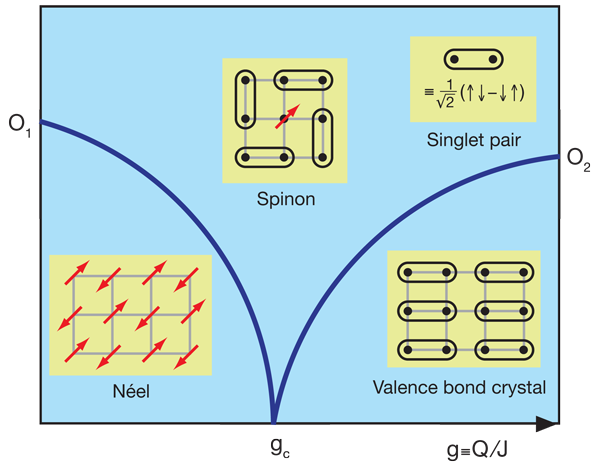
The hypothesized phenomenon of “deconfined quantum criticality” (DQC) [7] represents a dramatic manifestation of these Berry-phase-related quantum interference effects in critical phenomena. Consider a system of interacting spins. Two conventional phases in these systems are (i) antiferromagnetically ordered phases, also called Néel phases, and (ii) valence bond crystal (VBC) phases, in which spins are paired into singlets and these singlet pairs are arranged in a pattern that breaks lattice translational symmetry (see Fig. 1). In both these phases, spin-half excitations called spinons are confined in bound pairs, somewhat in the way that quarks are confined in quantum chromodynamics (although the precise details are different).

At DQC [7] due to Berry phase effects, there can be a phase transition between Néel and VBC phases, where both order parameters vanish continuously from the two sides, and right at the critical point, free or “deconfined” spinons arise (see Fig. 1). In the theory of phase transitions developed by Landau, Ginzburg, and Wilson, critical fluctuations are associated with the order parameter fields that describe the bulk phases, and this precludes direct continuous transition between two unrelated ordered phases, except by fine-tuning of parameters [1]. However, in the case of DQC, the critical fluctuations are associated with the spinon field, which is like the square root of the Néel order parameter. It brings with it an arbitrary phase, which turns into a local gauge freedom in the theory and gives rise to a gauge field that is like a photon. As soon as the Néel order disappears, on sufficiently long length scales, these photon fields lead to the emergence of VBC order [7].

But can the validity of DQC be confirmed by numerical simulations on model systems? Excluding the case of one spatial dimension, which is special for a variety of reasons and where lack of order and excitations with fractional quantum numbers is the rule rather than the exception, compelling evidence for DQC has been difficult to come by and indeed arguments to the contrary have been presented [8].

Early numerical studies using series expansions [9], showed that when a Néel phase is disordered due to a combination of frustration and quantum fluctuations, the Néel order parameter goes continuously to zero and a spin-singlet phase with a gap to spin excitations emerges. However, progress in the field has been slowed by lack of computational methods that can study long length scale fluctuations and hence distinguish between a weakly first order and a genuinely second order transition, and calculate critical exponents in the case of the latter.

In 2007, this situation was remedied by Anders Sandvik of Boston University in the US, who proposed a novel “ $J$ - $Q$ ” model [10], with a nearest-neighbor Heisenberg exchange of strength $J$ and a four-spin plaquette interaction of strength $Q$ . This model exhibits a phase transition from a Néel to a VBC phase, and is amenable to large-scale quantum Monte Carlo simulations. However, the simulation results have remained controversial [11].

Writing in Physical Review Letters, Sandvik now presents [12] results of the most extensive simulations to date. The data make a compelling case that there is a direct continuous transition between Néel and VBC phases, as needed for DQC. However, there is an unusual and unanticipated aspect to the data, which possibly relates to uncertainties in previous studies. Several thermodynamic properties are shown to exhibit logarithmic corrections to scaling. In the renormalization group theory of phase transitions [1], such logarithmic corrections arise only in very special cases, and they were not anticipated by existing DQC theory in this case [7]. Hopefully, this study will stimulate further theoretical and computational work in this direction.

The experimental case for deconfined quantum criticality is also unsettled. It is possible that fractionalization of quantum numbers and emergence of novel excitations right at the critical point, related to the Berry phases, is a common theme in many kinds of quantum phase transitions, such as those observed between an antiferromagnet and a fermi-liquid metal in heavy fermion systems [13], or between a variety of proposed phases in the high-temperature superconducting cuprates [14]. However, itinerant fermions bring with them additional complexity and it is difficult to unambiguously relate these transitions to DQC.

Hence, it would be nice if direct transitions between Néel and valence bond phases could be found in real materials. Triangular and kagome lattice based materials with spin-half are good candidates for such phenomena [15] and indeed there is evidence for dimerization in some cases [16]. However, it is not easy to drive experimental systems through a phase transition at $T = 0$ without impurities, doping, or magnetic fields, each of which brings in additional features. Perhaps organic molecular crystals, which are very sensitive to pressure, are the most promising candidates.

On the theoretical side, there is a need for more models where DQC can be established [17], as well as for novel theoretical and computational methods to study them. Recent tensor-network based methods are promising in this regard [18]. One would also like to see direct numerical evidence for deconfined fractionalized degrees of freedom. Previous simulations [10] have shown evidence for emergent photons that should accompany spinons [7], but the spinons themselves have not been looked for.

References

M. E. Fisher, Rev. Mod. Phys. 46, 597 (1974)
D. Bitko et al., Phys. Rev. Lett. 77, 940 (1996)
S. Sachdev, Quantum Phase Transitions (Cambridge University Press, Cambridge, United Kingdom, 1999)[Amazon][WorldCat]
N. Read and S. Sachdev, Phys. Rev. B 42, 4568 (1990)
Z. Fisk et al., Science 239, 33 (1988)
P. W. Anderson, Science 235, 1196 (1987); P. A. Lee et al., Rev. Mod. Phys. 78, 17 (2006)
T. Senthil et al., Science 303, 1490 (2004); Phys. Rev. B 70, 144407 (2004)
A. B. Kuklov et al., Phys. Rev. Lett. 101, 050405 (2008)
R. R. P. Singh et al., Phys. Rev. B 60, 7278 (1999); Z. Weihong et al., 59, 14367 (1999)
A. W. Sandvik, Phys. Rev. Lett. 98, 227202 (2007)
R. G. Melko and R. K. Kaul, Phys. Rev. Lett. 100, 017203 (2008); F. J. Jiang, J. Stat. Mech. P02009 (2008)
A. W. Sandvik, Phys. Rev. Lett. 104, 177201 (2010)
A. Schroder et al., Nature 407, 351 (2000)
S. Chakravarty et al., Phys. Rev. B 63, 094503 (2001); C. M. Varma, Phys. Rev. Lett. 83, 3538 (1999)
Y. Shimizu et al., Phys. Rev. Lett. 91, 107001 (2003); M. Tamura and R. Kato, J. Phys. Condens. Matter 14, L729 (2002); R. Coldea et al., Phys. Rev. Lett. 86, 1335 (2001); J. S. Helton et al., 98, 107204 (2007)
Y. Shimizu et al., J. Phys. Condens Matter 19, 145240 (2007); K. Morita et al., J. Phys. Soc. Jpn. 77, 043707 (2008)
D. N. Sheng, O. I. Motrunich, and M. P. A. Fisher, Phys. Rev. B 79, 205112 (2009)
G. Evenbly and G. Vidal, arXiv:0904.3383

About the Author

Rajiv R. P. Singh is Professor of Physics at the University of California at Davis. He received his Ph.D. in physics in 1986 from the State University of New York at Stony Brook. He was then a postdoctoral researcher at Cornell University, at the University of Maryland, and at AT&T Bell Labs in Murray Hill, New Jersey. He joined the physics faculty at the University of California at Davis in 1989. He became a fellow of the American Physical Society in 2006. His research interests include studies of quantum phases of matter and biological physics.