Hidden one-dimensional physics in 2D critical metals
The Landau Fermi-liquid theory [1] has been the workhorse of the physics of interacting electrons for over 50 years. Its main postulate is that low-energy fermions in the vicinity of the Fermi surface are long lived and can be treated as sharp quasiparticles: their energy scales linearly with k-kF, while the inverse lifetime scales as a higher power of k-kF [e.g., as (k-kF)2 in three dimensions], and remains parametrically smaller near kF , regardless of the strength of the actual screened Coulomb interaction. Perturbation theories of electron-electron interaction in dimensions larger than 1 reproduce the Fermi liquid, so something special has to be done to a system to destroy it.
The search for a non-Fermi-liquid in dimensions D>1 was originally stimulated by the discovery of non-Fermi-liquid behavior in the nonsuperconducting phase of high- Tc cuprates. This quest has now grown into a much broader area of correlated electron physics and in recent years has led to many exciting new developments. An important new finding in this field has been reported in two high-quality Physical Review B articles by Maxim Metlitski and Subir Sachdev from Harvard University [2,3].
One of the ideas floating around from the early days of high- Tc superconductivity is that a non-Fermi-liquid in D>1 emerges when fermions are interacting with a band of gapless, overdamped bosons [4,5]. Such a situation emerges when a Fermi liquid reaches a critical point towards a density-wave instability (e.g., an instability towards an itinerant ferromagnetism [6], or towards a quadrupolar, nematic-type order [7]), and in theories of fermions interacting with a gauge field (for instance, a field that connects spin and charge properties) [4,5,8–10]. In all these cases, the problem reduces to fermions interacting, via a constant coupling g, with a bosonic field whose susceptibility as a function of momentum q and frequency Ω has the form χ-1(q,Ω)=q2-iγΩ/q (in this case, the dynamical exponent z=3; the dynamical exponent z occurs in the power-law relation between typical q and typical Ω∼qz). This interaction can be judged by how it affects fermionic and bosonic excitations via the corresponding self-energies and vertex corrections. The perturbation theory to second order in g shows an interesting behavior—bosonic excitations and static fermionic excitations remain essentially unaffected, but the dynamical fermionic self-energy Σ(kF,ω), which accounts for the fermionic lifetime, is singular in dimensions of 3 or less, and in the most studied 2D case behaves, as a function of frequency ω, as (1+i√3)ω2/3 [4–7].
Taken at face value, this result implies that the fermionic damping and the fermionic energy remain of the same order (k-kF)3/2, no matter how close k is to the Fermi surface—that is, fermionic excitations never become sharp. This contradicts the key postulate of the Fermi liquid. The intriguing question then is whether ω2/3 is the exact form of the self-energy. For a long time it was thought that this was the exact form. The two-loop Feynman diagram for the self-energy also gives ω2/3, and power-counting arguments indicate that ω2/3 is reproduced to all orders in perturbation theory. By itself, this is not the proof that ω2/3 survives, as the perturbation series does not necessarily converge. But several authors argued [5,9] that loop expansion can be put under control by extending the theory to a large number of fermionic flavors N and by taking the limit N>>1, like high-energy physicists often do. In the large- N limit, the prefactor for the two-loop ω2/3 term becomes (logN/N)2<<1, and by power counting, higher-order contributions should be progressively smaller in 1/N. The theory then becomes controllable and in many respects similar to the Eliashberg theory for electron-phonon interaction [11], which is the canonical tool that physicists use to analyze phenomena such as superconductivity. Indeed, extending from N=1 to large N is only a theoretical trick. But there is also physical reasoning involved—after rescaling, N appears as the overall factor in the curvature of the 2D Fermi surface, and the curvature in turn appears in the denominators of multiloop diagrams. The smallness of higher-order ω2/3 terms is then a consequence of the fact that curvature-dependent 2D processes with scattering between different parts of the Fermi surface play the major role.
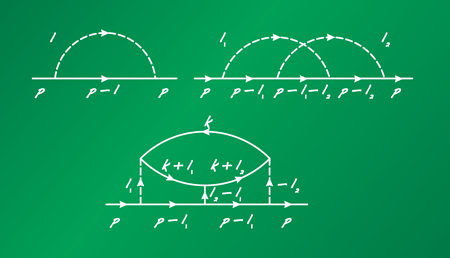
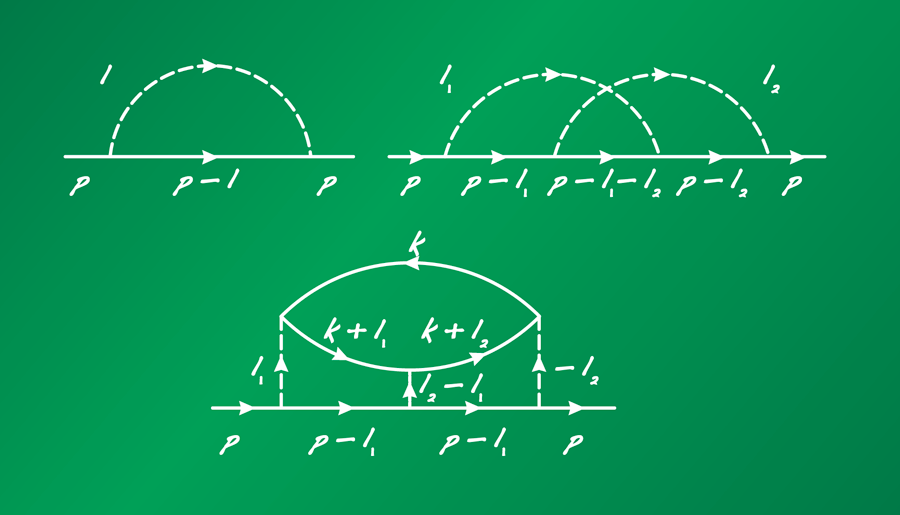
For about 15 years it was thought that the problem had been solved, i.e., for a large class of physical problems ω2/3 is the exact form of the fermionic self-energy in a non-Fermi-liquid, just like ω+iω2 is the exact form of the self-energy in a conventional 3D Fermi liquid. If so, then system properties in the non-Fermi-liquid phase are known exactly—a theorist’s dream. However, in 2009 Sung-Sik Lee from McMaster University, Canada, looked at the problem from a field theory perspective and found [12] that the victory lap was premature—there is an infinite subset of ω2/3 diagrams, beginning from the third order, in which the curvature is canceled out; as a result, there is no smallness of 1/N in the prefactor. An example of such a diagram is presented in Fig. 1. In field theory terminology, these special diagrams form the subset of planar diagrams. From a physical perspective, they represent processes that are strictly one-dimensional (either forward or backward scattering), despite the system itself being two-dimensional. In other words, the result by S.-S. Lee implies that there is “hidden one-dimensionality” in 2D systems—while most of the processes contributing to fermionic self-energy are two-dimensional (and small in 1/N), some are strictly one-dimensional (and not small in 1/N). By itself, hidden dimensionality is not specific to non-Fermi-liquid behavior—the same hidden one-dimensionality actually also affects Fermi-liquid behavior [13], and was shown a few years ago to be responsible for nonanalytic temperature and magnetic field dependences of the specific heat and the spin susceptibility in a Fermi liquid [14].
The discovery by S.-S. Lee brought the theory into unexplored territory. On one hand, the fermionic self-energy Σ(kF,ω) is still ω2/3, even with planar diagrams. On the other, there is no small parameter to put the theory under control. It was still possible, though, that the ω2/3 form of the self-energy survives. In their first paper, Metlitski and Sachdev show [2] that this is not the case, and hidden 1D processes change the physics qualitatively, not just quantitatively. They explicitly compute self-energy at third order and demonstrate that, although Σ(kF,ω)∝ω2/3, the self-energy at ω=0 is Σ(kF,0)∝(k-kF)log|k-kF|, again without 1/N in the prefactor, and that the three-loop vertex correction is also logarithmically singular. They argue that, at four-loop order, Σ(kF,ω) also acquires an extra logarithm and becomes ω2/3logω. The presence of logarithms is the qualitatively new effect—it shows that the ω2/3 form of the self-energy is not reproduced at higher orders, contrary to the belief in the community over so many years.
Metlitski and Sachdev [2] have gone further in their analysis and used scaling arguments to argue that the logarithms give rise to a singular renormalization of the quasiparticle residue (the strength of the quasiparticle pole), such that the full fermionic Green’s function near the Fermi surface has the form
where a is a constant, and η=O(1) is the anomalous dimension. This analysis was further extended by Mross et al. [15], who found an elegant way to put the calculation of η under control.
In the same paper [2], Metlitski and Sachdev also analyze the form of bosonic self-energy, specifically the renormalization of the q2 term in the static bosonic propagator. The question they asked is whether the critical point is by itself stable. It has been known before that the corrections to the q2 term are singular near a ferromagnetic instability in an SU(2) spin-invariant Fermi liquid, such that the system necessarily experiences a preemptive transition [16]. But for the cases of the instability in the charge channel (e.g., towards a charge nematic), or Ising-like ferromagnetic instability, which Metlitski and Sachdev considered, singular corrections all cancel out, and only regular q2 corrections remain. It was widely believed that these q2 corrections were innocent, but Metlitski and Sachdev showed that hidden one-dimensionality again makes a difference: the q2 corrections from three-loop planar diagrams are negative and contain an extra factor of N1/2, i.e., they are large. Whether these large corrections destroy the critical behavior and lead to a preemptive instability, as in the ferromagnetic case, still remains to be seen, but the result of Metlitski and Sachdev and the complimentary analysis by Mross et al. [15] clearly show that there is a potential problem here that needs to be resolved.
In their second paper [3], Metlitski and Sachdev extended the analysis to an antiferromagnetic Q=(π,π) instability in a 2D Fermi liquid. This problem was intensively studied in the context of optimally doped and overdoped cuprates, both for the normal state and magnetically mediated pairing. The underlying model is similar, but not identical, to the one discussed above—it now describes the interaction between fermions located near particular points at the Fermi surface (the hot spots, for which kF and kF+Q are on the Fermi surface) and their collective spin excitations with χ-1(q,Ω)=(q-Q)2-iγΩ (the dynamical exponent z=2). This spin-fermion model has been analyzed previously within the 1/N expansion by Abanov et al. [17]. Metlitski and Sachdev partly confirmed but partly corrected that analysis—they demonstrated that the dynamical exponent gets renormalized and flows away from z=2.
The key element of the Metlitski-Sachdev study of the antiferromagnetic model is their analysis of the validity of the Eliashberg theory. Earlier works assumed that multiloop corrections form a series in 1/N and only extra powers of logarithms appear. Metlitski and Sachdev argued that the same “hidden” 1D physics that affected the behavior of the critical models with soft bosonic fluctuations at q=0 also affects the behavior of an antiferromagnetic spin-fermion model. To demonstrate this, they constructed a q=0 fluctuation out of two q=Q fluctuations and reexpressed higher-order processes in terms of small- q scattering.
Do these corrections completely destroy the earlier Eliashberg-type analysis, or is there still an intermediate regime in which Eliashberg theory is valid to a good numerical accuracy? We don’t know yet, but one thing is clear—quantum-critical behavior in itinerant electron systems turns out to be much more involved than it was thought before the work of Metlitski and Sachdev. How to deal with 1D processes embedded into 2D systems is an open issue, but given current high interest in this problem, there is a good chance that the model of 2D fermions interacting with gapless collective excitations will be finally solved.
Note added by author (21 September 2010): References to two influential early works on 2D fermions coupled to a gauge field were missing in the original text and have now been inserted.
References
- See, for example, L. D. Landau, E. M. Lifshitz, and L. P. Pitaevski, Statistical Physics (Pergamon Press, Oxford, 1980)[Amazon][WorldCat]
- M. A. Metlitski and S. Sachdev, Phys. Rev. B 82, 075127 (2010)
- M. A. Metlitski and S. Sachdev, Phys. Rev. B 82, 075128 (2010)
- P. A. Lee, Phys. Rev. Lett. 63, 680 (1989)
- B. L. Altshuler, L. B. Ioffe, and A. J. Millis, Phys. Rev. B 50, 14048 (1994); Y. B. Kim, A. Furusaki, X-G Wen, and P. A. Lee, Phys. Rev. B 50, 17917 (1994)
- J. Rech, C. Pépin, and A. V. Chubukov, Phys. Rev. B 74, 195126 (2006)
- This issue has been studied by many authors. For recent reviews see M. Zacharias, P. Wölfle, and M. Garst, Phys. Rev. B 80, 165116 (2009); E. Fradkin, S. A. Kivelson, M. J. Lawler, J. P. Eisenstein, and A. P. Mackenzie, arXiv:0910.4166, and references therein
- T. Senthil, Phys. Rev. B 78, 035103 (2008)
- J. Polchinski, Nucl. Phys. B 422, 617 (1994)
- C. Nayak and F. Wilczek, Nucl. Phys. B 417, 359 (1994); 430, 534 (1994)
- G. M. Eliashberg, Sov. Phys. JETP 16, 780 (1963)
- S.-S. Lee, Phys. Rev. B 80, 165102 (2009)
- A. V. Chubukov, S.-S. Lee, and Y.B. Kim (unpublished)
- H. v. Löhneysen, A. Rosch, M. Vojta, and P. Wölfle, Rev. Mod. Phys. 79, 1015 (2007), and references therein
- D. F. Mross, J. McGreevy, H. Liu, and T. Senthil, arXiv:1003.0894
- D. Belitz, T. R. Kirkpatrick, and T. Vojta, Rev. Mod. Phys. 77, 579 (2005); A. V. Chubukov and D. L. Maslov, Phys. Rev. Lett. 103, 216401 (2009)
- A. Abanov, A. V. Chubukov, and J. Schmalian, Adv. Phys., 52, 119 (2003)