A landmark proof

Frank  Wilczek

Viewpoint

A landmark proof

Center for Theoretical Physics, Massachusetts Institute of Technology, 77 Massachusetts Avenue, 6-301, Cambridge, MA 02139, USA

February 7, 2011• Physics 4, 10

Researchers finally prove the conjecture that the low-energy excitations of some quantum Hall states are non-Abelian anyons.

Figure caption — **Figure 1:** Different aspects of the topology, or “braiding,” of virtual worldlines in two spatial dimensions. The horizontal direction represents time, the vertical and out of page directions represent the two spatial dimensions available to the particles. Thus our three spatial dimensions allow a convenient representation of the worldlines for particles moving in two spatial dimensions. (a) Two indistinguishable particles can change places with either one passing over the other. These two kinds of histories are topologically distinct; neither can be continuously deformed into the other. (b) There is a natural multiplication operation on braids, which turns the topologically distinct classes of braids into a group (the braid group). The multiplication operation illustrated here is simply to glue the separate braids together.

In a paper published in Physical Review B, Parsa Bonderson and Chetan Nayak from Microsoft Station Q at the University of California at Santa Barbara, and Victor Gurarie from the University of Colorado, provide a long-sought proof that quasiparticles in certain quantized Hall states are non-Abelian anyons [1]. To appreciate their achievement, it will be helpful to review the basic concepts of what anyons are and how they are realized in quantum Hall states, and also to clarify the meaning, in this context, of “proof.”

What are anyons? In quantum theory, the physics of indistinguishable particles displays fundamentally new features that have no analog in classical physics. Specifically: A process wherein the initial state has particles at positions ( $A$ , $B$ ) while the final state has particles at ( $A^{'}$ , $B^{'}$ ) can take place through either of two distinct pathways. Indeed, if we follow (in our minds) the worldlines of the (virtual) particles we might discover either $(A, B) \to (A^{'}, B^{'})$ or $(A, B) \to (B^{'}, A^{'})$ . If we do not actively observe the intermediate states, we must add the amplitudes for those distinct possible pathways to the same final physical state. Classical physics, which guides us in calculating the relative contributions of nearby trajectories, does not suggest a unique rule for their relative weight. Two consistent rules are simply to add them, corresponding to bosons, or to add them with a relative factor $- 1$ , corresponding to fermions.

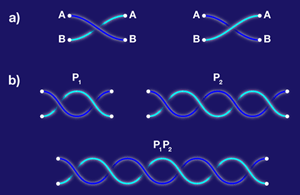
For particles that are constrained to move in a two-dimensional plane, the classification of discretely different (i.e., topologically distinct) pathways is more elaborate. It is governed by the braid group. As shown in Fig. 1(a), histories with $(A, B) \to (B, A)$ can be achieved with the first particle either passing over or passing under the second particle. In three (or more) spatial dimensions, it is possible to interpolate continuously between those two kinds of histories, with ends held fixed, by maneuvering in the spare dimension to avoid any crossing. But in two dimensions, we must consider infinitely many topologically distinct classes, distinguished according to the integer multiple of $π$ through which the relative coordinate winds. When this integer is even, we have $(A, B) \to (A, B)$ , when it is odd, we have $(A, B) \to (B, A)$ ; that distinction, of course, survives in higher dimensions, but the finer classification collapses.

It is natural to define multiplication of pathway topologies $P_{1}$ , $P_{2}$ by gluing them together into longer pathways, as shown in Fig. 1(b). It is not hard to see that the topological class of the product $P_{1} P_{2}$ is independent of the choice of particular pathways to represent $P_{1}$ and $P_{2}$ . It is also not hard to see that the multiplication operation defines a group, with the inverse of topological class $P$ containing the time-reversed versions of its paths.

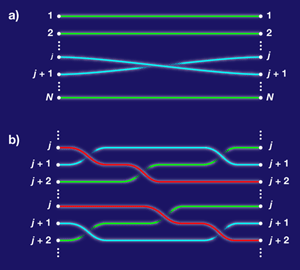
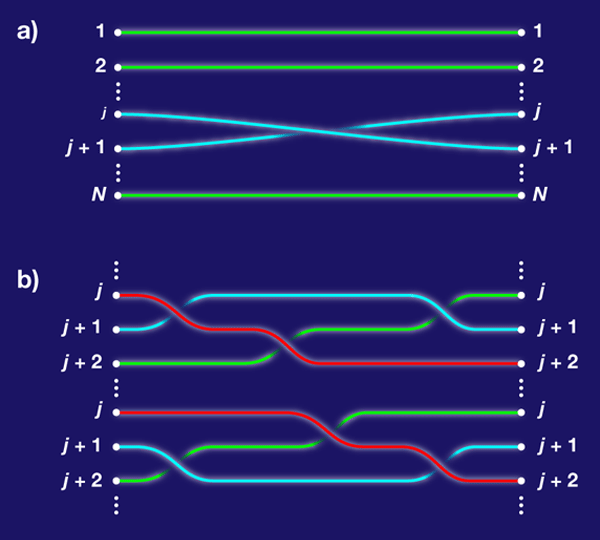
All these concepts generalize straightforwardly to the case of $N$ indistinguishable particles. Putting those particles in some reference order, we define elementary operations $σ_{j}$ , wherein particle $j$ winds through $π$ around particle $j + 1$ , avoiding all the others, as in Fig. 2(a). Then one can show—this is not so easy!—that all possible path topologies are generated by taking products of the $σ_{j}$ and their inverses, subject only to the relations

The second of these relations, whose geometric content is made visible in Fig. 2(b), is known as the Yang-Baxter relation. These generators and relations define the braid group. In three or more spatial dimensions, one has also $σ_{j}^{2} = 1$ for all $j$ , as discussed above.

In setting up the quantum mechanics of indistinguishable particles, it is consistent to weight the topologically distinct classes of trajectories according to any representation of the braid group. We can take, for example,

for all $j$ . In this formulation, $θ = 0$ (mod $2 π$ ) corresponds to bosons, and $θ = π$ (mod $2 π$ ) corresponds to fermions; but more generally any angle $θ$ is consistent with the general principles of quantum theory, and thus we speak of anyons [2].

One can also consider multidimensional representations of the braid group. A particularly important one is given by

where the matrices $γ_{j}$ obey the Clifford-Dirac algebra

The size of the matrices $γ_{j}$ needed to realize this algebra is $2^{[N - 1] / 2}$ ; in particular, it grows exponentially with $N$ .

Quantum statistics can be considered as a very special kind of interaction. This sort of interaction is determined entirely by large-scale, global (topological) aspects of particles’ trajectories. This makes it separate and distinct from ordinary interactions, which are highly local. In particular, the statistical interaction affects even distantly separated particles; in this sense, it is a long-range interaction. Also, because the statistical interaction only monitors global properties of the particle motion, it is robust against a wide variety of perturbations. Thus anyons embody a form of quantum coherence that is stable, yet open to controlled manipulation. These complementary virtues make them promising as a substrate for quantum computing.

The two realizations, Eqs. (3) and (4), exemplify Abelian and non-Abelian anyons, respectively. For Abelian anyons the statistical interaction only multiplies amplitudes by numbers. In this it represents a fairly straightforward generalization of Bose and Fermi statistics; it is simply that we allow complex phases, not just $\pm 1$ . For non-Abelian anyons, the statistical interaction multiplies by matrices, not merely numbers. Thus it involves an expanded Hilbert space; to describe the many-body state, given the positions of the particles, we must also specify a location in a nontrivial—in our example, $2^{[N - 1] / 2}$ -dimensional—Hilbert space. Very loosely speaking, it is as if the particles develop an additional internal degree of freedom, analogous to spin. That formulation does not quite do justice to the situation, however. One sign of this is that the dimension of the Hilbert space doubles only when we add two new particles, as if they contribute a single “joint spin,” though they may be far apart. Considered more accurately, the new degrees of freedom encode subtle, spatially distributed properties of the many-body wave function. One can also have “quantum statistical” interactions between different kinds of particles, sensitive to how their worldlines entangle.

Since ordinary particles fundamentally exist in three dimensions, they are either bosons or fermions, even if they happen to be constrained, say by a potential, to move in two dimensions. Anyons can only arise, therefore, in essentially two-dimensional states of matter where the localized states of low energy—the quasiparticles—are collective excitations involving correlations among many electrons. Such quasiparticles are candidate anyons.

To date, the theory of the quantum Hall effect has been the most fruitful and reliable source of anyons. That theory has three aspects: intuitive, macroscopic, and microscopic. The overall intuitive picture is that in the quantum Hall effect, electrons organize themselves into an incompressible liquid whose preferred density is proportional to the ambient magnetic field. More detailed intuition comes from guessing many-electron wave functions that are esthetically attractive. (This is much less arbitrary than it might sound, because holomorphy and homogeneity constrain the choices.) The macroscopic theory—in the jargon, the “effective” theory—also involves inspired guesswork. Inspired by the intuitive picture and wave functions, one formulates model quantum field theories that consistently embody the expected low-energy excitations and their properties, and makes deductions from the models. Finally, the microscopic theory is based on finding sensible Hamiltonians (i.e., local, and based on few-body interactions) for which the attractive wave functions demonstrably describe the low-energy states. Although the real-world Hamiltonian, which contains impurities, effects of extraneous (bulk) electrons, etc., is more complicated and less tractable than the model Hamiltonian, some “universal” quantities, including the quantum statistics of quasiparticles, are insensitive to small perturbations, and for these one can extrapolate from the model to reality reliably. That defines, in this context, the standard of proof.

Abelian anyon statistics of the simplest quantum Hall states, at filling fractions $ν = 1 / (2 p + 1)$ , were derived from a microscopic theory in the earliest calculations of this kind [3]. The quantum statistics emerged as a geometric or “Berry” phase accompanying the adiabatic motion of well-separated quasiparticles. Calculating the value of that phase required evaluation of a formidable-looking definite integral. Fortunately, that integral could be reduced, using Cauchy’s theorem in complex variable theory, to estimation of the density of the quantum Hall fluid. Now the rigidity (incompressibility) and quantized value of that density is the central feature of the intuitive theory of the quantum Hall effect; indeed, it basically rephrases the observed quantization of the Hall conductivity. Mathematical proof, however, requires demonstration that the microscopic wave function in fact exhibits that density. For the relatively simple microscopic wave functions at $ν = 1 / (2 p + 1)$ this crucial fact can be argued directly.

In more complicated cases, however, including all known non-Abelian examples, direct calculation of the required integrals seems out of reach. This mathematical difficulty has stood in the way of a genuine microscopic derivation of non-Abelian anyons, even for quantum Hall states where the macroscopic theory strongly suggests their existence [4–6]. Bonderson, Gurarie, and Nayak’s work, a tour de force of physical insight and mathematical ingenuity, has broken through that barrier. They exploit, in particular, a clever alternative realization of their microscopic wave functions as the partition function of a system of particles interacting by Coulomb’s law—a system for which extensive numerical and analytical results are available. At last, the anticipated properties of these particles, weird and unprecedented as they are, have a firm mathematical foundation. Now we eagerly await the next great step: experimental confirmation.

References

P. Bonderson, V. Gurarie, and C. Nayak, Phys. Rev. B 83, 075303 (2011)
A. Stern, Ann. Physics 323, 204 (2008)
D. Arovas, J. R. Schrieffer, and F. Wilczek, Phys. Rev. Lett. 53, 722 (1984)
G. Moore and N. Read, Nucl. Phys. B 360, 362 (1991)
C. Nayak and F. Wilczek, Nucl. Phys. B 479, 529 (1996)
D. Ivanov, Phys. Rev. Lett. 86, 268 (2001)

About the Author

Frank Wilczek is Herman Feshbach Professor of physics in the Center for Theoretical Physics at MIT. He obtained his B.S. in mathematics at the University of Chicago, and M. A. in mathematics and Ph.D. in physics at Princeton University. He has been Professor of physics at Princeton University, Robert Huttenback Professor of physics and member of the Institute for Theoretical Physics at the University of California, Santa Barbara, and J. Robert Oppenheimer Professor of physics at the Institute for Advanced Study, Princeton. His research interests span a wide range of areas in theoretical physics.