Strong Staggered Flux Lattices for Cold Atoms

Erich J. Mueller

Viewpoint

Strong Staggered Flux Lattices for Cold Atoms

Erich J. Mueller

Laboratory of Atomic and Solid State Physics, Cornell University, Ithaca, NY 14853, USA

December 12, 2011• Physics 4, 107

Extremely high magnetic fields have been simulated by laser manipulation of atoms trapped in an optical lattice.

Figure caption — **Figure 1:** (Bottom) Schematic of the tight-binding model realized by Aidelsburger *et al.* in their cold-atom experiment [1]. Red and blue spheres (labeled by A and B) denote sites. Arrows in the middle of plaquettes show the direction of the effective magnetic field. (Top) Schematic of the optical lattice potential with period two superlattice in the $x$ direction used in the experiment. The large detuning between the red sites and blue sites prevents tunneling in the $x$ direction. Two external lasers are introduced, whose detuning coincides with the energy mismatch, restoring tunneling. Phases from these lasers lead to the staggered effective magnetic field appearing in the tight-binding model.

Electrons in magnetic fields move in circular orbits. These gyrations are key to a wide range of physical phenomena: superconducting vortices, quantum magnetoresistance oscillations, Hall effects, etc. Theoretical (see 25 April 2011 Viewpoint) and experimental (see 30 March 2009 Viewpoint) advances have begun to make possible “artificial magnetic fields” that allow this physics to be studied using cold neutral atoms. As they report in Physical Review Letters, Monika Aidelsburger at Ludwig Maximilian University, Germany, and colleagues have reached an important milestone in the creation of artificial magnetic fields [1], producing a quantum degenerate gas of interacting bosons that experiences the analog of a large staggered flux.

Electrons on a lattice are often described by tight-binding models, where the charge carriers move by hopping between spatially localized single-particle states. Magnetic fields appear as phases on the hopping matrix elements [2]. In their experiment on neutral rubidium- $87$ atoms, Aidelsburger et al. mimic the effect of a magnetic field by using techniques from quantum optics (described below) to generate such phases. Their success opens up several new areas of study with cold atoms; most importantly the interplay of lattices and magnetic fields, analogs of the quantum Hall effects, and band-structure physics related to topological insulators.

The “effective magnetic field” generated in these experiments is extremely strong. One of the most important dimensionless measures of the field strength in a lattice system is the magnetic flux through a single square unit cell or plaquette. For particles of charge $q$ , this flux is is $ħ φ / q$ , where $φ$ is the sum of the phases on the four hopping matrix elements encountered when hopping around the boundary of the plaquette, $ħ = h / 2 π$ , and $h$ is Plank’s constant. (In other contexts, this relation between phases and flux gives rise to the Aharanov-Bohm effect, whereby an interference experiment can be used to detect a magnetic field.) Since $φ$ is only defined modulo $2 π$ , its largest possible magnitude is $π$ . Here the atoms encountered a phase $| φ | = π / 2$ . If Aidelsburger et al. were actually working with electrons (as opposed to atoms), and the lattice was of atomic dimensions, this would correspond to a magnetic field well above $1000$ tesla. Such fields are impossible to achieve in condensed-matter experiments, but theorists speculate that they would lead to rich phenomena, for example, in a uniform field, the single-particle spectrum is fractal [3]. Hints of this fractal spectrum have been seen in high-mobility nanofabricated structures [4]. Adding interactions, as is readily done in the cold-atom setting, should make the physics even more interesting, and lead one into uncharted territory. How is the quantum Hall effect modified by Mott physics, or by the fractal single-particle spectrum? Future experiments will explore such questions.

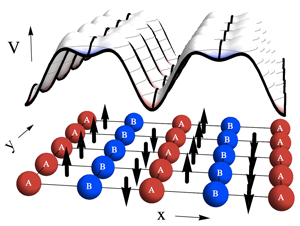
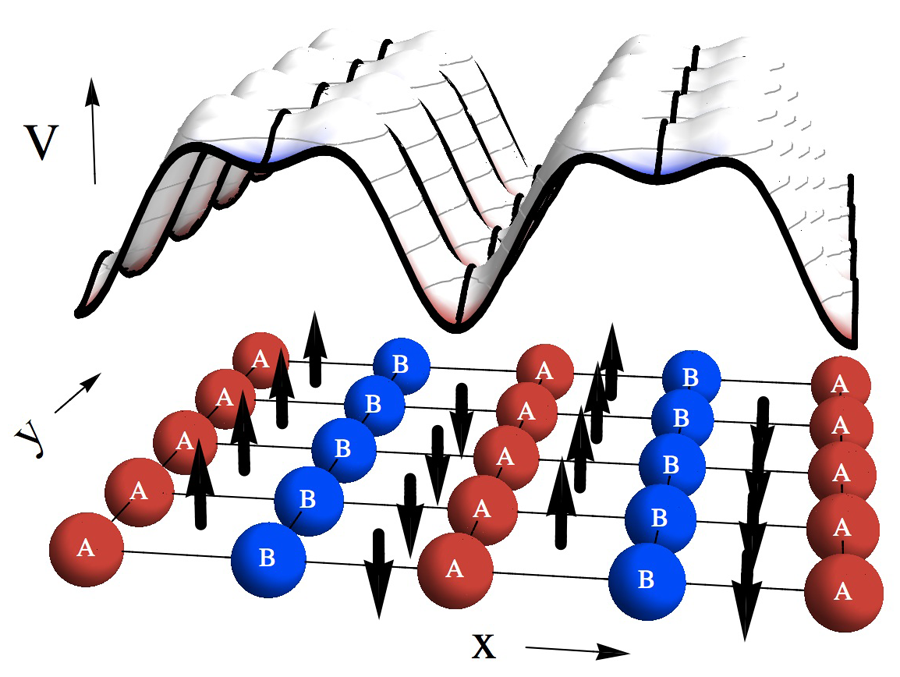
Even more striking, Aidelsburger et al. produced a staggered field: As illustrated in Fig. 1, their system acts as if the magnetic field oscillates from plaquette to plaquette. One consequence is an unusual band structure describing the atoms, with two overlapping bands that touch at two “Dirac points.” Small modifications to this lattice can introduce gaps between the two bands at these Dirac points, producing a band structure in which phases accumulate when one adiabatically moves around closed paths in quasimomentum space. These phases act similarly to an applied magnetic field, producing “anomalous Hall effects” and, under appropriate circumstances, giving rise to an insulator with nontrivial topological invariants [5]. Even though there is no net magnetic field, Aidelsburger’s lattice breaks time-reversal symmetry and is very similar to a model introduced by Haldane [6], which has inspired recent work on “topological insulators” (see 28 November 2011 Viewpoint). Similar staggered flux lattices spontaneously appear in models of spin liquids and strongly correlated electron systems [7]. It is very exciting to contemplate using cold atoms to study analogs of this physics in a more controlled setting.

To generate their effective magnetic field, the authors first used lasers to create the potential illustrated in Fig. 1, where in the $x$ direction there is a bias between alternate sites (labeled A and B). The energy difference between the A sites and B sites is large compared to the bandwidth, effectively “turning off” tunneling in the $x$ direction. To turn tunneling back on, Aidelsburger et al. introduce two more lasers, carefully tuned so that an atom can resonantly absorb a photon from one beam, emit it into the other, and hop in the $x$ direction. The lasers are skewed with respect to one another, so that the relative phase between the two beams varies in space. This phase difference translates into spatially dependent phases on the hopping matrix elements. By varying the angle between these beams the “flux” can be varied.

An equivalent picture is that the two-photon process gives the atoms an impulse in the $y$ direction when they jump from a row of A sites to B sites. Interpreting this impulse in terms of a Lorentz force gives the effective magnetic field. The direction of the field alternates because the direction one hops to get from A to B alternates.

To demonstrate that they have created staggered fluxes, Aidelsburger et al. studied the momentum distribution of a Bose-Einstein condensate in this lattice. They found that as they changed the ratio of the strength of the hopping in the $x$ and $y$ direction, they could tune from a regime where condensation involved only a single quasimomentum to a regime where two different quasimomenta were involved—the latter occurring when the $x$ hopping, denoted $K$ , was much weaker than the $y$ hopping, $J$ . They found quantitative agreement with the tight-binding band structure and with detailed theoretical studies by Möller and Cooper [8].

By slightly modifying their setup, Aidelsburger et al. were also able to carry out dynamical experiments on an array of isolated $4$ -site plaquettes, each of which contained a single atom. Such studies of small clusters are another important frontier [9].

The idea of using “Raman assisted hopping” to mimic a magnetic field was first suggested by Jaksch and Zoller [10]. As they pointed out, one produces a uniform field, rather than a staggered field, if one replaces the superlattice with a linear potential. Each hop in the positive $x$ direction will then involve the same impulse. Alternative approaches are described in detail in a recent review article by Dalibard et al. [11].

There have been two other successful methods of generating analogs of magnetic fields for cold atoms. First, the Coriolis force has the same form as the Lorentz force, allowing experiments on rotating gases to explore vortex physics. In rotation experiments, the strength of the “magnetic field” is limited by instabilities caused by the centrifugal force. Second, a group of scientists at the National Institute for Standards and Technology has produced a continuum system where two-photon Raman transitions are used to emulate a vector potential [12]. In the coming years, artificial electromagnetic fields will play an ever-increasing role in cold-atom experiments.

Acknowledgments

This material is based upon work supported by the National Science Foundation under grant No. PHY-1068165.

References

M. Aidelsburger, M. Atala, S. Nascimbène, S. Trotzky, Y-A. Chen, and I. Bloch, Phys. Rev. Lett. 107, 255301 (2011)
R. Peierls, Z. Phys. 80, 763 (1933)
D. Hofstadter, Phys. Rev. B 14, 2239 (1976)
T. Feil et al., Phys. Rev. B 75, 075303 (2007); M. C. Geisler et al., Phys. Rev. Lett. 92, 256801 (2004); S. Melinte et al., 92, 036802 (2004)
D. Xiao, M.-C. Chang, and Q. Niu, Rev. Mod. Phys 82, 1959 (2010)
F. Haldane, Phys. Rev. Lett. 61, 2015 (1988)
S. Chakravarty, R. B. Laughlin, D. K. Morr, and C. Nayak, Phys. Rev. B 63, 094503 (2001)
G. Moller and N. R. Cooper, Phys. Rev. A 82, 063625 (2010)
D. Blume, arXiv:1111.0941 (2011); Rep. Prog. Phys (to be published)
D. Jaksch and P. Zoller, New J. Phy. 5, 56 (2003)
J. Dalibard, F. Gerbier, G. Juzeliūnas, and P. Öhberg, Rev. Mod. Phys. 83 1523 (2011)
Y.-J. Lin, R. L. Compton, K. J. Garcia, J. V. Porto, and I. B. Spielman, Nature 462, 628 (2009)

About the Author

Erich Mueller is an associate professor in the Laboratory of Atomic and Solid State Physics at Cornell University http://people.ccmr.cornell.edu/~emueller/. He received his Ph.D. in 2001 from the University of Illinois at Urbana-Champaign, and completed a postdoctoral fellowship at the Ohio State University. He conducts theoretical research on ultracold gases. In 2009 he was recognized as an Outstanding Referee by the American Physical Society.