A Well-Rounded Life for an Electron Spin

Michael  E. Flatté

Viewpoint

A Well-Rounded Life for an Electron Spin

Michael E. Flatté

Department of Physics and Astronomy, University of Iowa, Iowa City, IA 52242, USA

September 19, 2011• Physics 4, 73

Electric-field control of the spin-orbit field in [111] quantum wells lengthens the spin coherence time.

Figure caption — **Figure 1:** Schematic depiction of spin-orbit fields as a function of electron crystal momentum in a zincblende quantum well grown along each of three special directions: (a) $[001]$ , (b) $[110]$ , (c) $[111]$ . The spin-orbit field from the quantum well symmetry is indicated in blue, and the electric-field-induced spin-orbit field is indicated in red. For (c) the two fields have the same momentum-dependent structure.

Coherent precession of the spins of conduction electrons in a semiconductor, a phenomenon known as conduction electron spin coherence, persists over time and length scales far longer than many other nonequilibrium phenomena in solids; room-temperature spin coherence times for conduction electrons can be more than $3$ orders of magnitude longer than coherence times associated with orbital motion [1]. Electron spin coherence in nonmagnetic semiconductors relaxes eventually through the spin-orbit interaction, a relativistic effect coupling the electron spin to its motion [2]. Andrea Balocchi at the University of Toulouse, France, and collaborators have now demonstrated a dramatic electric-field control of the spin coherence time [3], through electrical manipulation of the spin-orbit interaction in a novel quantum well geometry. This work, appearing in Physical Review Letters, clarifies the behavior of the spin-orbit interaction in quantum wells and may permit new spintronic devices that rely on manipulation of spin coherence.

In these experiments a spin-polarized nonequilibrium distribution of electrons is generated by a short pulse of circularly polarized laser light, whose energy is tuned to the band gap of the quantum well. The spin-orbit interaction, which governs the electron spin lifetimes, also generates optical selection rules that lead to circularly polarized light generating spin-polarized conduction electrons and valence holes [4]. When these nonequilibrium electrons and holes recombine over the next few nanoseconds to create photoluminescence, the same selection rules lead to circularly polarized light emission. The strong spin-orbit interaction associated with valence states also leads to rapid spin relaxation for the holes, so the light emission polarization is predominately associated with the electron spin polarization. A magnetic field applied perpendicular to the nonequilibrium spin polarization causes the spins to precess, yielding an oscillating photoluminescence polarization as the population recombines [5].

The spin relaxation of conduction electrons in nonmagnetic semiconductors with inversion-asymmetric crystal lattices originates from effective pseudomagnetic fields generated by the spin-orbit interaction. As time-reversal symmetry holds for the nonmagnetic semiconductor, these strange effective magnetic fields, called spin-orbit fields, must change sign when the electron momentum changes sign. Such momentum-dependent spin-orbit fields will cause the electron spin to precess around various different precession axes as the electron moves about within the conduction band and changes its momentum by scattering off of dirt, dopants, or excitations such as phonons. Spin-orbit fields can even generate coherent, controlled precession in addition to reducing the electron spin coherence time [6]. Electric-field control of spin-orbit fields in quantum wells grown along certain special symmetry directions has been predicted [7,8] and demonstrated [9,10] to control the persistence time of spins oriented along a specific, chosen fixed axis, however, the effect on a precessing spin is considerably less [11]. The key to the dramatic reduction of the spin relaxation rate for a spin oriented in any direction observed by Balocchi et al. was the choice of an unusual quantum well symmetry: a growth axis oriented parallel to the $[111]$ direction of the crystal lattice.

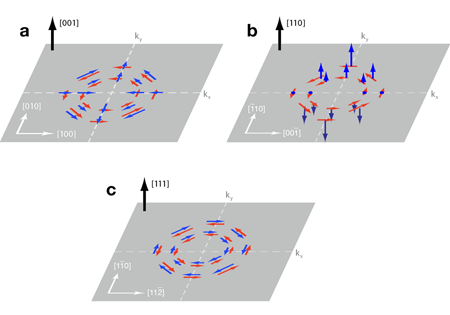
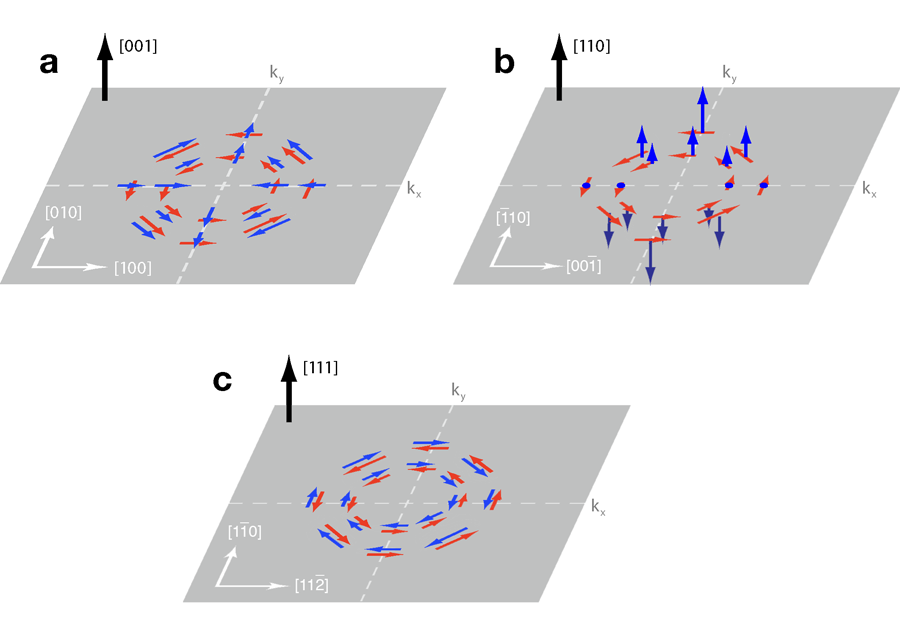
Figure 1 shows the spin-orbit fields to the lowest order in electron momentum for two commonly explored quantum wells, with growth axes along the $[001]$ and $[110]$ crystal axes, as well as the $[111]$ quantum well. For the $[001]$ quantum well of Fig. 1(a), the spin-orbit field is oriented in-plane, with the symmetry indicated by the blue arrows. An applied electric field parallel to the growth direction produces a new spin-orbit field, referred to as the Rashba field [12], which is shown in red. For a proper choice of the Rashba field, the spin-orbit field can be made entirely parallel to the $[\bar{1} 10]$ direction, which would cause no relaxation for a spin parallel to $[\bar{1} 10]$ . However, a precessing spin would still be sensitive [11] to the (now larger) spin-orbit field oriented along $[\bar{1} 10]$ . For the $[110]$ quantum well of Fig. 1(b), the spin-orbit field is entirely out-of-plane, as indicated by the blue arrows. For this quantum well, in the absence of an electric field, a spin oriented parallel to $[110]$ would not relax through this mechanism, unless an electric field were applied. Electric-field tuning ranges for spins oriented along the $[110]$ direction in a $[110]$ quantum well have been shown to be at least a factor of $10$ near room temperature, but again the coherence time of a precessing spin would still be sensitive to the spin-orbit field of the quantum well and the tuning range for the spin coherence time would be much less [8].

The situation for the $[111]$ quantum well explored by Balocchi et al. is quite different. Here the symmetry of the spin-orbit field of the quantum well and that of the Rashba field are identical, and thus, for a proper choice of electric field, the two will cancel. This increases the spin coherence time for precessing spins by at least a factor of $10$ at $50 K$ . They demonstrated the effect by growing their quantum well within a $p n$ junction, which permitted the application of a controlled electric field. By reversing the orientation of the quantum well within the $p n$ junction they excluded artifacts such as a lengthening of the electron spin coherence time by changing the electron-hole overlap with the electric field (electron spin coherence times are very sensitive to the presence of holes). The use of an undoped quantum well also excludes the sensitive dependence of the electron spin coherence time on doping [4] from explaining their results.

Ideally, this initial demonstration would be extended to a much larger tuning range for the spin coherence time, and also observed at room temperature. A larger tuning range could, in principle, be achieved with a larger electric field; however, this large electric field may cause the electrons to leak out of the quantum well. Electron leakage might be reduced by considering a quantum well material system that confines the electrons much more strongly, such as an $InAs$ well with $AlSb$ barriers.

As the temperature rises in the quantum well of Balocchi et al., the electron distribution spreads out to larger crystal momenta, which creates new challenges. The special symmetry of the $[111]$ quantum well only holds to lowest order in the electron momentum; the next-order term cannot be canceled by the Rashba field. For nondegenerate electrons in the quantum well, the relative importance of the next-highest-order spin-orbit fields to the lowest-order fields for the spin relaxation rate is proportional to $T^{2}$ . At room temperature, therefore, the relative importance of the uncontrollable contribution to the spin relaxation will increase $\sim 40$ times over its importance at the highest temperature ( $50 K$ ) at which spin coherence control was demonstrated by Balocchi et al. The quantum well can be made narrower to readjust the importance of these two contributions, but a narrower quantum well requires a larger electric field to tune, as seen by Balocchi et al. when they compared a $15 nm$ quantum well to a $7.5 nm$ quantum well.

In addition to the first demonstration of the lengthening of spin coherence times due to electric-field control of the spin-orbit fields these results may lead to new semiconductor spintronic devices. Electric-field tuning of spin relaxation forms the basis for turning the current on and off in some spin transistor proposals [13], and can help initialize electron-spin-based quantum computers [14,15]. This recent work moves these proposals closer to realization, although the tuning range would need to be $\sim 10^{5}$ , and for the spin transistor application the relevant operating temperature is room temperature.

Acknowledgment

This work was supported by an ARO MURI.

References

J. M. Kikkawa, I. P. Smorchkova, N. Samarth, and D. D. Awschalom, Science 277, 1284 (1997)
Y. Yafet, Solid State Phys. 14, 1 (1963)
A. Balocchi, Q. H. Duong, P. Renucci, B. L. Liu, C. Fontaine, T. Amand, D. Lagarde, and X. Marie, Phys. Rev. Lett. 107, 136604 (2011)
Optical Orientation, edited by F. Meier and B. P. Zakharchenya (North-Holland, New York, 1984)[Amazon][WorldCat]
M. Oestreich, S. Hallstein, A. P. Heberle, K. Eberl, E. Bauser, and W. W. Rühle, Phys. Rev. B 53, 7911 (1996)
Y. Kato, R. C. Myers, A. C. Gossard, and D. D. Awschalom, Nature 427, 50 (2004)
N. S. Averkiev and L. E. Golub, Phys. Rev. B 60, 15582 (1999)
W. H. Lau and M. E. Flatté, J. Appl. Phys. 91, 8682 (2002)
O. Z. Karimov, G. H. John, R. T. Harley, W. H. Lau, M. E. Flatté, M. Henini, and R. Airey, Phys. Rev. Lett. 91, 246601 (2003)
N. S. Averkiev, L. E. Golub, A. S. Gurevich, V. P. Evtikhlev, V. P. Kochereshko, A. V. Platonov, A. S. Shkolnik, and Yu. P. Efimov, Phys. Rev. B 74, 033305 (2006)
W. H. Lau and M. E. Flatté, Phys. Rev. B 72, 161311 (2005)
E. I. Rashba, Sov. Phys. Solid State 2, 1109 (1960)
K. C. Hall and M. E. Flatté, Appl. Phys. Lett. 88, 162503 (2006)
D. Loss and D. P. DiVincenzo, Phys. Rev. A 57, 120 (1998)
B. E. Kane, Nature 393, 133 (1998)

About the Author

Michael E. Flatté received the A.B. in Physics from Harvard and the Ph.D. in Physics from the University of California, Santa Barbara, advised by Walter Kohn. After a postdoctoral year at the Institute for Theoretical Physics at UC Santa Barbara and a postdoctoral fellowship at Harvard University’s Division of Applied Sciences he joined the faculty at The University of Iowa in 1995. Michael E. Flatté is a Fellow of the American Physical Society and the American Association for the Advancement of Science and is the F. Wendell Miller Professor of Physics at The University of Iowa. Professor Flatté is an expert in condensed matter and materials theory, specializing in carrier and spin dynamics and their applications to novel semiconductor devices. His research foci include semiconductor spintronics, solid-state quantum computation, carrier dynamics in semiconductor nanostructures, and nanoparticle dynamics in heterogeneous liquids. He has over 135 publications as well as 12 review articles/book chapters, 4 patents, and one edited book.