The Smallest Thermal Machines
Are there limits to how small one can make a thermodynamic machine? At first sight, this question appears to contradict itself, as thermodynamics usually begins with a kind of macroscopic picture. However, as Nicolas Brunner at the University of Bristol, UK, and colleagues describe in a paper appearing in Physical Review E, this constraint can be circumvented, if one focuses on a special kind of architecture [1].
As a starting point, we may think of a nanoscopic object like a single molecule or even a two-level system (qubit) being in contact with a large heat bath. This contact will ultimately lead to a local thermal equilibrium between the object and the bath. (Temperature controls the relative occupancy of the energy states on the qubit.) We may also imagine a situation where a nanoscopic object interconnects two baths with different temperatures, thus enabling a heat current [2].
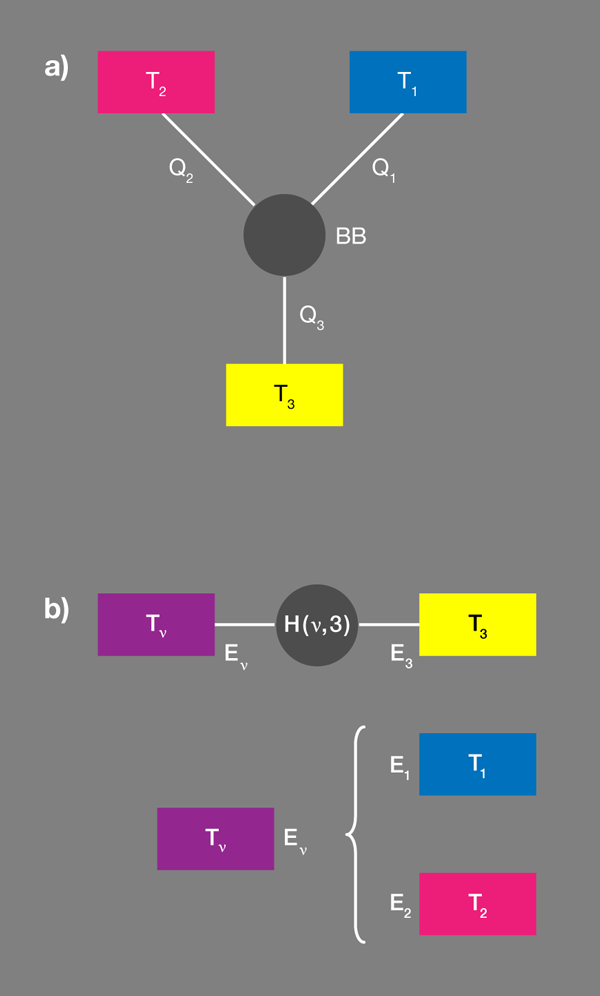
Taking this one step further, we can build up the ingredients of a fundamental thermodynamic machine by connecting three separate baths with a nanoscopic node—a black box that is designed to exchange heat between the baths in a particular way [Fig. 1(a)]. By definition, baths can only interchange heat and we’ll assume the box cannot store energy, so heat currents to or from the three heat baths have to add up to zero. Clearly, this could not happen if the box was just another heat bath.
Let’s imagine this black box has three separate “sockets,” each represented by a two-level qubit that can have an energy , , or , respectively. Let’s also assume there is an interaction between the three qubits that allows them to transmit energy to each other, but that these transitions are constrained by . Put differently, socket can’t be excited unless socket transfers its energy to socket . This machinery, which is a consequence of the socket qubits being correlated with one another on the most elementary level, is all we need to produce an energy switch, which can, for example, act as a heat pump.
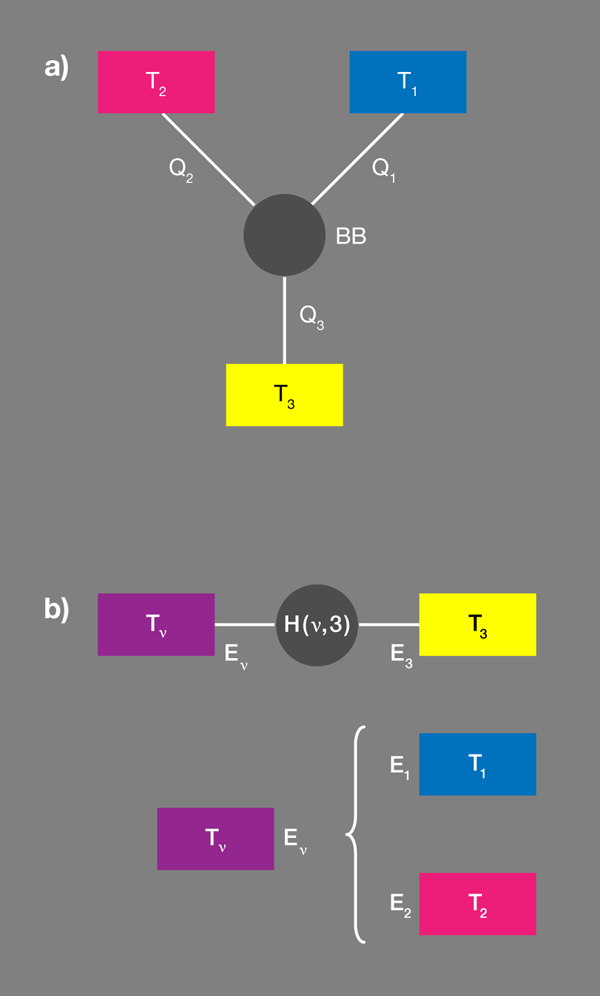
Brunner et al. propose a convenient tool [1] for designing these correlations by introducing the concept of a “virtual qubit” with a “virtual temperature” [Fig. 1(b)]. Within each qubit we arbitrarily select a pair of states, which thus specifies an effective spin or qubit. The quantum system is thus reduced to three qubits with fixed occupation probabilities. Grouping any two qubits makes an effective four-level system. Out of the possible transitions within the resulting enlarged system there is but one two-particle transition, which would involve the transfer of energy between the two subsystems considered. This new qubit is the “virtual qubit.” The transfer energy will be nonzero, if the energies associated with the original two qubits are different, as the authors assume.
The probability that the virtual qubit is in a particular state is fixed by its virtual temperature. As for any two-level system, the probability that the higher energy state is occupied relative to the probability that the lower energy state is occupied is ). In the present case, this temperature is neither a local temperature of a real subsystem, nor does it relate to the four-level composite subsystem as a whole. In this sense it is virtual, and it can be positive or negative.
So far, this is only a partial description, nothing is going to happen, no currents. But now Brunner et al. ask what happens if this virtual qubit, with its virtual temperature, is resonantly coupled to a third qubit, which is in contact with its own bath . They assume the coupling is weak and can be modeled by a specifically designed interaction Hamiltonian. (The assumption of weak coupling makes sure that each level is still predominantly localized in one of the subsystems.)
Effectively, this brings us back to the picture of two baths interconnected by an effective node: we expect a flow of heat, the direction of which is dictated by thermalization. It seems as though nothing is new.
Nothing new? Let us go back to the full description, in which there are three qubits and three separate baths with temperatures , , . By choosing the spectra of the qubits and local temperatures one can design various values to make particular thermodynamic machines. Let’s focus on the interesting scenarios where heat either flows out from the coldest bath or into the hottest bath (note that negative temperatures, which occur in systems with a finite number of states and corresponds to a hotter temperature than a positive one, are possible [3]).
For the device to operate reversibly, the two systems in contact should have the same temperature, i.e., . This is the Carnot limit. Slightly away from this limit, internal heat currents flow and the device works in different ways, depending on the temperatures of the baths. When , Brunner et al. show that heat flows from the coldest bath to the intermediate bath , while the hot bath serves as an external driver. This is a refrigerator for the bath—or a heat pump for the bath. When , heat flows from the intermediate bath to the hottest bath , with the waste heat being dumped into the coldest bath . This function may be seen as a kind of heat transformation: Low temperature heat is converted into high temperature heat [4]. Indeed, in the quantum domain, such cooling by heating has attracted renewed interest [5,6], but such heat distributions have macroscopic analogs in the adsorber refrigerator and heat converter, respectively [4].
What about the third operational mode, the heat engine? Here, an explicit account of work (as output) is needed. The challenge is to find a generalization of the concept of work versus heat that fits Brunner et al.’s model, but at the same time agrees with the standard definition of work.
The authors suggest this generalization is possible by referencing negative virtual temperatures, which amounts to inverting the occupation probabilities for the two states in the virtual qubit [1]. (The idea is reminiscent of the condition for light amplification in a laser.) However, in my opinion, this interpretation is open to question. First, inverting the probabilities amounts to characterizing a state, but work (as well as heat) should characterize a process, not a state. Second, negative temperatures need not be special: As Brunner et al. mention, a virtual qubit with negative temperature coupled to a bath with a finite number of spins (that is, a system with a finite number of states) would simply lead to a thermal equilibrium at this negative temperature [7]. Lastly, in a typical classical heat engine, work enters as an external force (on the piston) time displacement. Quantum mechanically, this is described as an explicitly time-dependent Hamiltonian [8]—a feature missing in Brunner et al.’s description.
But the present methodology does have the advantage that one can analyze potential deviations from the ideal performance (the Carnot limit), even under otherwise optimal conditions (e.g., low speed). The argument runs roughly as follows: The interacting three-qubit model has to be fine-tuned in order to reach the Carnot-limit, so under which conditions does this model best approach reality? The answer is that each qubit must physically be a two-level system. Any model where the qubits have more than one transition will lead to a large set of varying virtual temperatures, which cannot all fit the requirements, and will decrease the overall efficiency.
On a conceptual level, Brunner et al. remind us that “phenomena” depend on how we look at them. Their model is a network of networks: One node, the virtual qubit, is, again, a two-qubit network. On a coarser-grained level (a virtual qubit plus a third qubit), we recognize simple heat transport. When we look closer at the three qubits separately, we see a heat engine. This has the potential to design new functionalities in open quantum networks, where the subsystems have different roles to play.
References
- N. Brunner, N. Linden, S. Popescu, and P. Skrzypczyk, Phys. Rev. E 85, 051117 (2012)
- A. Buldum, D. M. Leitner, and S. Ciraci, Europhys. Lett. 47, 208 (1999)
- P. T. Landsberg, J. Phys. A 10, 1773 (1977)
- P. Srikhirin, S. Aphornratana, and S. Chungpaibulpatana Renew. Sustain. Energy Rev. 5, 343 (2001); see also the famous Szilard-Einstein refrigerator
- Y. X. Chen and S. W. Li, Europhys. Lett. 97, 40003 (2012)
- A. Mari and J. Eisert, arXiv:1104.0260; Phys. Rev. Lett. (to be published)
- G. Waldherr and G. Mahler, Europhys. Lett. 89, 40012 (2010)
- T. D. Kieu, Phys. Rev. Lett. 93, 140403 (2004)