Quasicrystals, Meet Topological Insulators
The 2011 Nobel Prize in Chemistry recognized Dan Shechtman’s pioneering work on quasicrystals—materials that are characterized by a long-range ordered tiling of atoms but aren’t periodic like conventional crystals. The award brought a rather unique field of research back into the focus of the science community. Since it began in 1984 [1], quasicrystals research has been a source of shared interest for crystallographers, materials scientists, chemists, physicists, and mathematicians, for whom working together was the rule, rather than the exception.
In Physical Review Letters, Yaacov Kraus and colleagues at the Weizmann Institute of Science in Israel describe experiments that open the umbrella of quasicrystals research even wider [2]. They demonstrate an unexpected mathematical connection between quasicrystals and topological insulators [3], a class of unconventional insulators with conducting surface states. Furthermore they show a practical example of this connection in an optical waveguide device that creates a quasiperiodic potential for light: because this device has “topological” properties, they are able to pump light across different optical channels into localized edge states. Kraus et al.’s finding of a connection between two seemingly different kinds of materials may deeply influence the way theorists design models to explore the physics of quasicrystals.
A topological insulator [3], like a conventional insulator, is a material with an electronic band gap, but its fundamental materials properties are insensitive to small changes in its materials parameters. Topological order is a generalization of the traditional classification schemes of solid phases, which are based on spontaneously broken symmetries (like the breaking of rotational symmetry that occurs when the spins in a material line up.) In contrast, a topological insulator may undergo a quantum phase transition that closes its band gap and changes its fundamental materials parameters, but no symmetry is spontaneously broken. In this sense, a topological insulator falls outside the traditional classification schemes for solid matter.
Topological insulators are classified by the mathematical properties of the Hamiltonians that describe them. Small changes in the materials parameters of a topological insulator are captured by a minor modification of its Hamiltonians, and the Hamiltonians describing all the topological insulators in a given “class” share characteristic properties of their spectra (band gaps, gapless surface states). But the same Hamiltonians cannot be simply deformed into the Hamiltonians of another topological class without changing the characteristic properties of their spectra, which is why topological insulators are insensitive to small changes in their materials properties. (This is similar to the way that a donut cannot be simply distorted into a sphere.)
This may sound like a mathematical distinction, but it has a measureable effect: The only way a topological insulator in one class can transition into another class—which is what must, for example, happen at the surface separating a three-dimensional topological insulator from vacuum—is over an intermediate metallic (zero-band-gap) state. As a result, two- and three-dimensional topological insulators have conducting edge and surface states, respectively. Perhaps the most famous example of these surface states is the integer quantum Hall effect (IQHE), where a two-dimensional sheet of electrons in a strong magnetic field has gapless edge states that carry the current [4].
So far, topological phases have mainly been studied theoretically or in a handful of materials and electronic devices. Kraus et al. have now extended the concept to quasicrystalline phases, and designed a photonics device that allows them to visualize the effects of such a connection [2]. They show that a tight-binding Hamiltonian for particles moving in a one-dimensional lattice that modulates their on-site or hopping interactions with a quasiperiodic potential (the Harper model) maps to a tight-binding Hamiltonian that can describe the two-dimensional IQHE. In this mapping, the bulk and edge states in the two-dimensional IQHE Hamiltonian have their respective counterparts in the bulk and edge states of the one-dimensional quasiperiodic Harper model.
Kraus et al. made an experimental version of such a one-dimensional quasiperiodic Harper model, which allowed them to study its band structure and optical states. To do this, they fabricated roughly 20 parallel semiconductor waveguides of varying widths on a semiconductor substrate. The waveguides were spaced closely enough together that when the authors introduced light into one waveguide, the evanescent part of the light field could tunnel into an adjacent waveguide. And, because the width of each waveguide determines its effective index of refraction, the whole array of waveguides acts as a quasiperiodic potential for the light.
In a series of experiments, the team introduced light into one waveguide and used a CCD camera to measure the distribution of light along the length of the device. They found that if they introduced light into one of the center waveguides, which corresponds to the bulk states of the corresponding quasiperiodic Hamiltonian, it would spread out. But if they introduced light into the leftmost or rightmost waveguide, which would correspond to the edge states of the quasiperiodic Hamiltonian crossing the gaps between the bulk states, it stayed on that side, thus demonstrating the peculiar nature of those optical edge states.
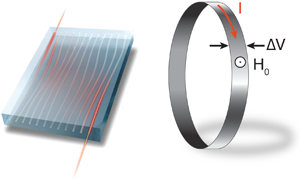
The authors found an interesting connection with the IQHE when they built a similar device in which the waveguides were not parallel but had a slowly varying separation between them along the length of the device (Fig. 1, left). This variation acted as a slowly varying phase in the quasiperiodic model that moves edge states from one edge to another; in their device, light introduced on the right side of the device gradually migrated to the left side.
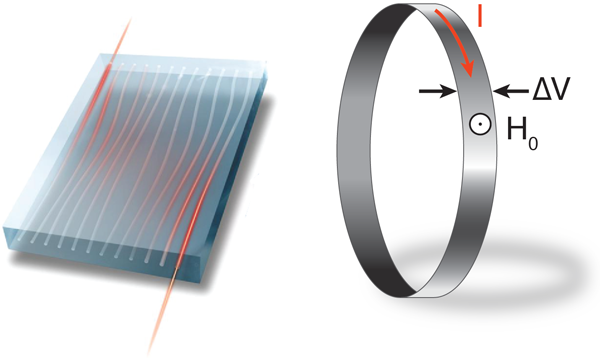
This migration is a well-known effect called “adiabatic pumping,” which the Nobel laureate Bob Laughlin [5] suggested to explain the IQHE [4]. In his picture, a slow variation in the magnetic flux piercing a two-dimensional ribbon (Fig. 1, right) pumps electrons in gapless edge states from one edge of the ribbon to the other. The fact that Kraus et al. see the same pumping effect in their optical device, which wouldn’t be possible if it were made of periodic waveguides, establishes the connection between quasiperiodicity in one dimension and the IQHE in two dimensions.
Kraus et al.’s work is relevant to a long-standing and fundamental problem of quasicrystals research. In the early days of studying quasicrystals, theorists tried to explain the geometrical properties of real quasicrystals with higher dimensional models—in some cases, with as many as 12 dimensions. But they viewed these higher dimensional models as merely handy mathematical tools, while the “real” physics of quasicrystals was described by Hamiltonians living in three spatial dimensions. But Kraus et al. have shown that higher-dimensional “ancestor” Hamiltonians have a measurable effect on the physics of lower-dimensional quasiperiodic systems.
The authors’ work also represents a new trend in quasicrystals research [6]. As opposed to studying the propagation of electrons in a quasicrystalline lattice, researchers are now looking at the propagation (or nonpropagation) of light or sound through complex materials that consist of basic components, such as metallic or semiconductor spheres, cones, or cylinders, arranged in a quasiperiodic fashion. In the long term, such composite systems will free quasicrystals research from the need to tile and decorate materials according to the laws of chemistry rather than the laws of higher-dimensional geometry. Instead, the ability to design new composite systems like photonic or phononic quasicrystals is only limited by the fabrication techniques, which are needed to put the components of these materials in the right place [7].
Lastly, we can ask if Kraus et al.’s results can be generalized to cover two- and three-dimensional quasiperiodic structures. In principle, their results should hold for any dimension and any topological index, which is the number that distinguishes one topological class from another. The quasiperiodicity in the Harper model is introduced by quasiperiodic modulation terms, and these terms have the effect of adding extra dimensions to the system. With respect to their topological properties, one may map these quasiperiodic model Hamiltonians to suitable higher-dimensional Hamiltonians, similar to the one-dimensional—two-dimensional correspondence that Kraus et al. found. Furthermore, the authors state that the Harper model may also be extended to one-dimensional quasiperiodic sequences like the Fibonacci sequence [2], which is very interesting, as the one-dimensional quasiperiodic sequences themselves may easily be extended to ways of decorating a lattice in higher dimensions [8]. In the long term, research along those lines and with focus on higher-dimensional Hamiltonians might even draw other fields, such as string theory, into the realm of quasicrystals research.
References
- D. Shechtman, I. Blech, D. Gratias, and J. W. Cahn, “Metallic Phase with Long-Range Orientational Order and No Translations Symmetry,” Phys. Rev. Lett. 53, 1951 (1984)
- Y. E. Kraus, Y. Lahini, Z. Ringel, M. Verbin, and O. Zilberberg, ”Topological States and Adiabatic Pumping in Quasicrystals,” Phys. Rev. Lett. 109, 106402 (2012)
- M. Z. Hasan and C. L. Kane, “Colloquium: Topological Insulators,” Rev. Mod. Phys. 82, 3045 (2010)
- K. v. Klitzing, G. Dorda, and M. Pepper, “New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance,” Phys. Rev. Lett. 45, 494 (1980)
- R. B. Laughlin, “Quantized Hall Conductivity in Two Dimensions,” Phys. Rev. B 23, 5632 (1981)
- W. Steurer and D. Sutter-Widmer, “Photonic and Phononic Quasicrystals,” J. Phys. D 40, R229 (2007)
- B. E. A. Saleh and M. C. Teich, Fundamentals of Photonics (Wiley, Hoboken, 2007)[Amazon][WorldCat]
- S. I. Ben-Abraham and A. Quandt, “Aperiodic Structures and Notions of Order and Disorder,” Philos. Mag. 91, 2718 (2011)