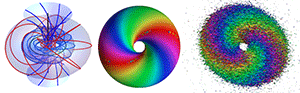
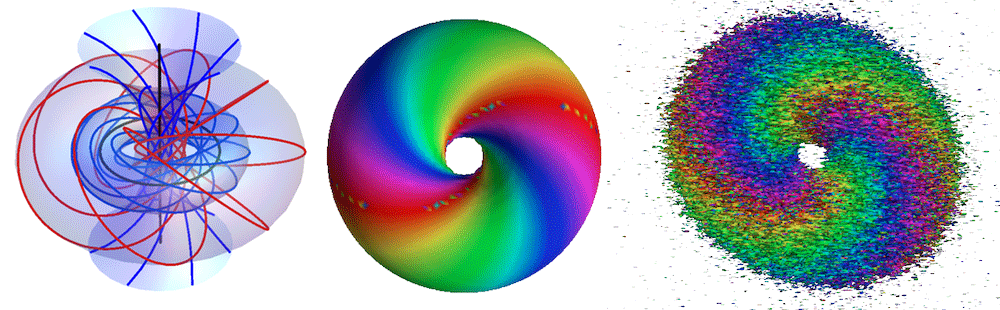Topology with Liquid Crystals
With lasers or electron beams, it is now possible to mold a variety of soft and hard materials into different shapes with new properties and functionalities. These techniques also provide some of the few ways to generate topological shapes from mathematics, like knots and vortices, in a real-world system. In Physical Review Letters, Bryan Gin-ge Chen of the University of Pennsylvania (now at Leiden University in the Netherlands) and colleagues demonstrate a new example of this approach [1]. Using a specially shaped laser beam, the researchers oriented the molecules in a liquid crystal such that the lines that follow their orientation—called the director field—formed a Hopf fibration (Fig. 1, left), a geometric shape that has fascinated scientists for more than 80 years [2]. Their experimental setup offers greater control over how this shape can be created, and under what conditions, than was previously possible. It could be used to understand how different boundary conditions affect the stability of the Hopf fibration, which has applications not only in abstract mathematics but also in fields like quantum physics and computer graphics.
Two objects are considered topologically distinct if there is no way to transform one to the other without cutting it or punching holes in it. For example, a coffee mug with a single hole in the handle and a donut are topologically equivalent, but a donut and a cookie are not. A material’s topology goes beyond its physical shape—it affects properties like light transmission, electrical conduction, or response to a magnetic field. These possibilities are inspiring researchers to find new ways to engineer materials with unusual topologies.
One way to make topological shapes is to sculpt them directly out of a material, using a technique such as optical laser lithography [3]. A different approach is to create spatial fields that are topological. For example, interfering light beams can be used to create lines of zero intensity that form knots and links [4]. Similarly, accelerating specially shaped hydrofoils through water can create flow lines that form isolated knots [5]. And in liquid crystals containing colloidal particles, the molecular field can entangle [6] and form microscopic knots of arbitrary complexity [7].
To make the Hopf fibration, Chen et al. spatially textured the molecular field in liquid crystals [2]. The special topological property of this object is that the streamlines of the field are mutually interlinked and twisted together. This makes it impossible to unwind the field into a homogenous configuration, where all streamlines are parallel to each other. In fact, the act of untwisting the Hopf fibration in one direction twists it more in another. An important distinction of the Hopf fibration is that the directions of the streamlines are continuous—meaning they don’t have any kinks or vanishing points. In contrast, the topological shapes that have been generated in optical, flow, or molecular fields have generally been associated with the varying (typically vanishing) magnitude of the field.
Chen et al. worked with chiral nematic liquid crystals, which are oily fluids consisting of rodlike molecules. The molecules align with their neighbors along a specific direction, called the director , which is a vector field with head-to-tail symmetry. But on large length scales, this director twists to form a helix. (More precisely, the existence of the helix depends on the confinement and the boundary conditions.) A feature of chiral nematic liquid crystals that makes them ideal for generating the Hopf fibration is that the nematic director is easily splayed, bent, or twisted by an external stimulus, bounding surface, or an optical field.
To form the Hopf fibration, Chen et al. sandwiched a -micron-thick layer of the molecules between two glass plates and guided the director field associated with the oriented molecules using holographic optical tweezers. Unlike conventional optical tweezers, which are hourglass-shaped light beams that can grip particles at their waist, the holographic variety have trapping fields with more complex shapes. The authors used this optical field to reorient the molecules away from the original homogeneous alignment and into a distorted molecular pattern. After switching off the field, they were able to see the molecules relax into a stable, inhomogeneous structure: the Hopf fibration. Specifically, by applying the optical field, they were able to break the symmetry of the original molecular pattern and change its topology. They were also able to form a topologically different structure, called the toron, which is characterized by two defect regions in the director field (see description in Ref. [8]).
A subtle point is that what makes up these shapes is not the individual nematic molecules, but their complex molecular orientational order, which becomes interwoven in a complex topological manner. To measure the direction of the field, Chen et al. used a type of fluorescence spectroscopy that depends on the orientation of the molecules with respect to the polarization of the illuminating light source.
But to show that the changing direction of the director field has the shape of the Hopf fibration, they had to develop a new way to display their measurements visually. Two angles are needed to define the orientation of the molecular field with respect to a fixed direction in space—in this case, the viewing direction of the microscope. Chen et al. represented these two angles with two elements: a surface and a color wheel. The shape of the surface is defined such that every point on it has the director perpendicular to the reference direction, while the colors on the surface correspond to points on a color wheel. (In their mapping, going from red to blue corresponds to the director rotating 120 degrees, but going from blue to red represents only a 60 degree change in the director.) Using their visualization technique, a Hopf fibration looks like a toroidal surface with color spirals, which is a simplified way to visualize the complex Hopf texture compared to more conventional representations. In principle, the same technique could be used to visualize other three-dimensional vector fields, such as magnetization or electric polarization.
The Hopf fibration is what is more formally referred to as a topological soliton because its twisted field lines can’t be smoothly transformed into straight ones. These objects have to obey Derrick’s theorem [9], which says that in bulk three-dimensional fields, the configuration can always lower its energy by shrinking. The object generated in Chen et al.’s experiment somehow circumvents this theorem: Once created, the Hopf fibration is stable and doesn’t change size. One possibility is that the geometry of the setup, which confines the Hopf fibration between two glass plates, is having an effect.
This and other questions could be addressed by seeing what happens to the fibration when it is scaled up or down in size. Another interesting possibility is to look at what happens to light when it is reflected or transmitted through the shape. Chiral nematic liquid crystals are already optically birefringent; these twisted states might be used to twist the polarization of light beams in a complex manner. There are also possible connections between the liquid crystals and what are called chiral ferromagnets [10], suggesting the Hopf fibration could be seen in a completely different system. Exploring these systems is of interest to both fundamental and applied sciences, and Chen et al.’s work shows that even abstract ideas in mathematics can influence materials science.
Correction (3 June 2013): Bryan Gin-ge Chen’s name and affiliation were corrected.
References
- B. G. Chen, P. J. Ackerman, G. P. Alexander, R. D. Kamien, and I. I. Smalyukh, “Generating the Hopf Fibration Experimentally in Nematic Liquid Crystals,” Phys. Rev. Lett. 110, 237801 (2013)
- H. Hopf, “Über die Abbildungen der dreidimensionalen Sphäre auf die Kugelfläche,” Math. Ann. 104, 637 (1931)
- J. Fischer and M. Wegener, “Three-Dimensional Optical Laser Lithography Beyond the Diffraction Limit,” Laser Photon. Rev. 7, 22 (2013)
- M. R. Dennis, R. P. King, B. Jack, K. O’Holleran, and M. J. Padgett, “Isolated Optical Vortex Knots,” Nature Phys. 6, 118 (2010)
- D. Kleckner and W. T. M. Irvine, “Creation and Dynamics of Knotted Vortices,” Nature Phys. 9, 253 (2013)
- M. Ravnik, M. Skarabot, S. Zumer, U. Tkalec, I. Poberaj, D. Babic, N. Osterman, and I. Musevic, “Entangled Nematic Colloidal Dimers and Wires,” Phys. Rev. Lett. 99, 247801 (2007)
- U. Tkalec, M. Ravnik, S. Copar, S. Zumer, and I. Musevic, “Reconfigurable Knots and Links in Chiral Nematic Colloids,” Science 333, 62 (2011)
- I. I. Smalyukh, Y. Lansac, N. A. Clark, and R. P. Trivedi, “Three-Dimensional Structure and Multistable Optical Switching of Triple Twist Toron Quasiparticles in Anisotropic Fluids,” Nature Mater. 9, 139 (2010)
- G. H. Derrick, “Comments on Nonlinear Wave Equations as Models for Elementary Particles,” J. Math. Phys. 5, 1252 (1964)
- J. Fukuda and S. Zumer, “Quasi-Two-Dimensional Skyrmion Lattices in a Chiral Nematic Liquid Crystal,” Nat. Commun. 2, 246 (2011)