Optical Boomerangs
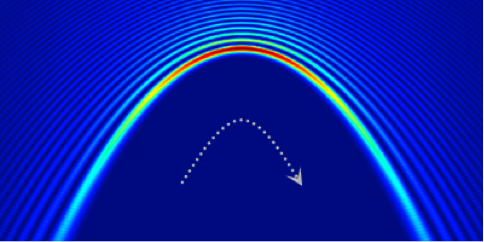
Optical beams that bend themselves in curves may, one day, guide intense plasmas along a desired path or help manipulate tiny particles. So far, researchers have studied these “self-accelerating” beams under somewhat limited conditions (see 28 November, 2007 Focus and 6 September, 2011 Viewpoint). In particular, they have been boxed in by the paraxial approximation: in order to make things work, the beams must bend only gradually, not straying far from the axis of propagation, otherwise the beams break up. In Physical Review Letters, two groups are now reporting generalized versions of these potentially useful curving beams that need not obey the paraxial limit.
It is known that nonparaxial beams can be exact solutions to the Helmholtz wave equation if they have a particular intensity profile, but these beams only travel in circular paths (see 16 April, 2012 Viewpoint). Peng Zhang at the University of California, Berkeley, and colleagues showed with theoretical calculations and experimental demonstrations that two other kinds of exact solutions also exist, called accelerating Mathieu beams (which propagate along elliptical paths and include circular nonparaxial beams as a special case) and accelerating Weber beams (which propagate along parabolic paths). As these beams bend themselves around these paths, they resist breakup by diffraction. To create the self-bending beams, Zhang et al. modified the intensity profile of a laser beam with a computer-controlled modulator. They then demonstrated the self-healing nature of these beams by partially blocking them with obstacles and watching the beams regroup and continue on their way.
In an independent report, Parinaz Aleahmad at the University of Central Florida, Orlando, and colleagues present calculations in which the Helmholtz equation is recast in terms of electric and magnetic vector potentials. With this fully vectorial approach, they demonstrate theoretically and experimentally the existence of two-dimensional beams that follow elliptical paths and are diffraction-free. In addition, Aleahmad et al. show that three-dimensional solutions exist that allow propagation of spherical wave fronts (among others), which also bend under certain conditions. – David Voss