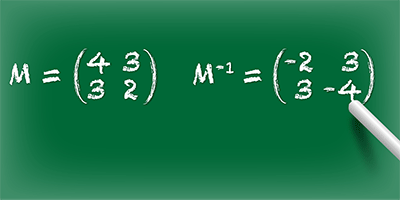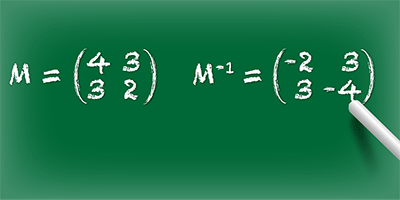Solving for and
It’s only three lines of simple math for a human, but a small victory for a quantum computer. Researchers in China report in Physical Review Letters that they can solve two linear equations by manipulating four entangled photons. Their demonstration—the rough equivalent of solving for and in the equations and —is the first proof that a quantum algorithm proposed in 2009, which promised exponential speed-up compared to one run on a normal CPU, can be implemented in the lab.
Few quantum algorithms are actually faster than their classical counterparts. The most famous example in which quantum mechanics wins is an algorithm for factoring large numbers proposed by mathematician Peter Shor in 1994. But four years ago, theorists showed that a quantum algorithm for solving a set of linear equations could also be exponentially faster that any classical algorithm, provided you only needed to know probabilistic information about the solution—and not the exact solution itself.
To implement this algorithm, Xindong Cai, at the University of Science and Technology of China in Hefei, and colleagues used a laser to prepare two pairs of entangled photons, which they spatially separated and sent down four different paths. Passing the photons through a series of logic gates effectively corresponded to the steps of solving two linear equations: inverting a matrix, multiplying it through, and calculating the two independent variables. The quantum computer is overkill for solving only two linear equations; the real advantages would come as the number of equations grows. – Jessica Thomas